TD 3
En python, les tableaux et les listes sont confondus. Dans ce TD, nous utiliserons indifférament le vocabulaire "tableau" ou "liste" pour parler des listes. On désignera par n la taille du tableau.
Exercice 1: Fonctionnement des listes
Décrivez la mémoire et l'affichage que vous obtiendrez si vous exécutez le code du programme suivant :
s = [0 , 0] t = s t[0] = 5 s[1] = 9 print( s ) print( t )
Exercice 2: Échange de deux valeurs dans un tableau
Écrire une procédure echange(t,i,j), où t est un tableau et i, j deux indices de ce tableau, qui modifie le tableau t de manière à ce que les valeurs contenues à la i-ième place et la j-ième place du tableau soient échangées.
Exercice 3: Algorithme mystère
Voici le code d'une procédure nommée mystere(t,i,p) prenant pour paramètres un tableau t et deux entiers positifs i et j :
def mystere(t,i,p):
if i+p >= len(t):
print("Erreur")
else:
for k in range(p):
echange(t,k+i,k+i+1)
Qu'effectue la procédure mystere(t,i,p) ? On pourra regarder l'effet de la fonction pour t=[3,4,0,1,8], i=0, p=3 ; puis pour le même t mais avec i=2 et p=2.
Exercice 4: Palindrome
Écrire une condition nécessaire et suffisante sur les t[i] pour que le tableau soit un palindrome.
Écrire une procédure palindrome(t) qui détermine si un tableau t est un palindrome, c'est-à-dire un tableau tel que lorsque l'on lit les cases "par indices croissants" (de 0 à n-1), on obtient la même séquence que si l'on lit les cases "par indices décroissants" (de n-1 à 0). (n est la taille du tableau.)
Par exemple, [3,4,1,4,3] et [12,0,4,8,8,4,0,12] sont des palindromes, mais [1,2,3,1,2,3] ou [4,6,6,4,2] ne le sont pas.
Exercice 5: Miroir
Écrire une procédure miroir(t) qui modifie un tableau t en son miroir. De manière plus précise, si t contient les valeurs t[0],t[1], ..., t[n-1] dans cet ordre, alors après exécution de miroir(t), t contiendra les valeurs t[n-1], t[n-2], ..., t[0] dans cet ordre.
Par exemple, si t=[3,4,0,1,8], alors la procédure miroir(t) modifie t en [8,1,0,4,3].
Exercice 6: Suites récurrentes
-
Écrire une procédure
suiteag(n)qui renvoie un tableautde longueurntel quet[k]soit lek-ième élément de la suite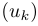 définie par
définie par 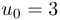 et pour
et pour 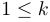 ,
, 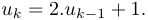
-
Écrire une procédure
fact(n)qui renvoie un tableautde longueurntel que![t[k] = k!](generated_images/idm2271.png) .
.
-
Écrire une procédure
fibo(n)qui renvoie un tableautde longueurntel quet[k]soit lek-ième nombre de Fibonacci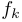 , défini par
, défini par 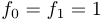 et pour
et pour 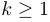 :
: 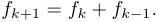
-
Écrire une procédure
sommepuissance(n,a)qui renvoie un tableautde longueurntel que![t[k] = \sum_{i=0}^k i^a.](generated_images/idm2286.png)
Exercice 7
Écrire une procédure add(t) qui modifie un tableau t en un tableau v de manière à ce que pour tout 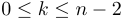 , on ait :
, on ait : ![v[k]=t[k]+t[k+1]](generated_images/idm2304.png) et
et ![v[n-1]=t[n-1]](generated_images/idm2305.png) .
.
Par exemple, si t=[3,4,0,1,8], alors la procédure add(t) modifie t en [7,4,1,9,8].
Exercice 8
Écrire une procédure add2(t) qui modifie un tableau t en un tableau 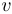 de manière à ce que pour tout
de manière à ce que pour tout 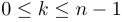 , on ait :
, on ait : ![v[k] = \sum_{i=0}^k t[i]](generated_images/idm2320.png) .
.
Exercice 9
Écrire une procédure add3(t) qui modifie un tableau t en un tableau v de manière à ce que pour tout 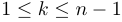 , on ait :
, on ait : ![v[k]=t[k]+t[k-1]](generated_images/idm2330.png) et
et ![v[0]=t[0]](generated_images/idm2331.png) .
.