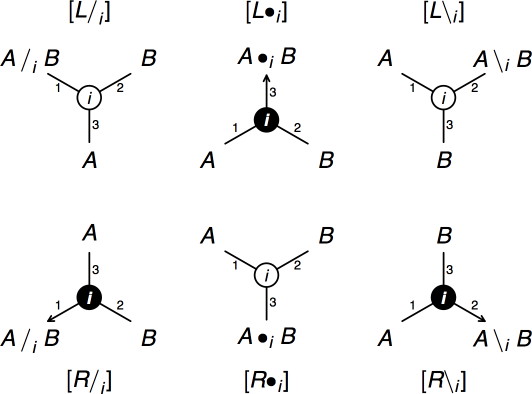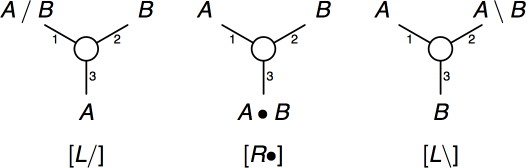
Figure 1. Links for AB grammars
A more technical introduction to proof nets for the multimodal Lambek calculus, which includes soundness, completeness and cut elimination proofs, can be found in Moot & Puite (2002).

Figure 1. Links for AB grammars
A link connects three nodes, each of which is labeled with a formula. The names of the links are shown below the rules. The distinctions between up and down and between left and right are important: the two nodes above a link are its hypotheses whereas the node below it is its conclusion. A link has a left hypothesis and a right hypothesis, with the left hypothesis displayed on the left and the right hypothesis on the right.
It is often useful to talk about the active formulas and the main formula of a link. The main formula is alway the complex formula, whereas the active formulas are its two subformulas. The difference between the three links in the figure is in the choice of the main formula. For the [L/] link, the main formula is the A/B formula (which is the left hypothesis of the link), for the [R•] link, the main formula is the A•B formula (which is the conclusion of the link) and for the [L\] link, the main formula is the A\B formula (which is the right hypothesis of the link).
The meaning of these links is as follows:
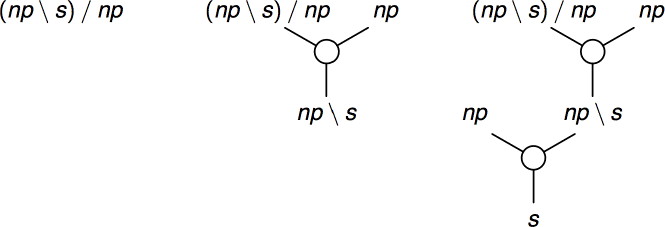
Figure 2. Unfolding a formula.
Note that all leaves, except the single (np\s)/np formula, are atomic. In the context of AB grammars the transitive verb formula corresponds to the formula assigned to a word in the lexicon: we will call it the lexical leaf. When looking at the tree on the right in the figure above, we see that some of the information in it is redundant: for example, we can determine the internal tree node has to be assigned the formula np\s simply based on its context: the adjacent np and s vertices are atomic and therefore they cannot be the main formula of this link. Knowing the internal node is assigned the formula np\s allows us to deduce that the lexical leaf has to be assigned to formula (np\s)/np.
If we replace the lexical leaf by one of the words in the lexicon to which the transitive verb formula is assigned, we have the tree shown in the figure below on the left. Remark that it is the same tree shown in the figure above on the right, with the simple addition of the word "follows" to the lexical leaf.
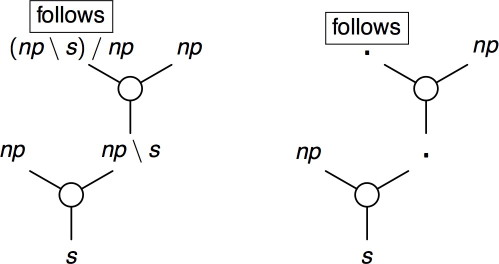
Figure 3. Mapping a proof structure into the corresponding abstract proof structure.
Now, when we suppres the redundant information the result is shown in the figure on the right: only the atomic formulas and the lexical leaf remain.
The tree on the left of Figure 3 called a proof structure, the tree on the right is its corresponding abstract proof structure. Proof structures and abstract proof structures do not necessarily correspond to proofs, in spite of what their name may suggest. We will see below how we can identify those proof structures which are correct, that is to say they correspond to sequent proofs or, equivalently, they are proof nets.
Grail uses abstract proof structures during its analyses and in the lexicon edit window.
For a lexical graph, like the one shown in Figure 3, there is not a lot of difference between a proof structure and an abstract proog structure, there is a direct 1-1 correspondence between the two. However, after a substitution, there is some information lost the abstract proof structure.
Now, we say a proof structure is correct or a proof net if all of its hypothesis leaves are lexical leaves and the conclusion is the required goal formula, s for sentence in most cases.
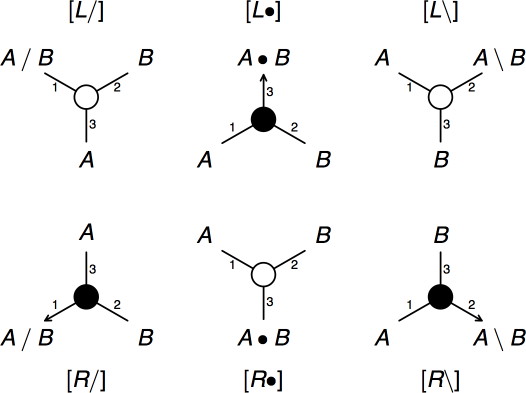
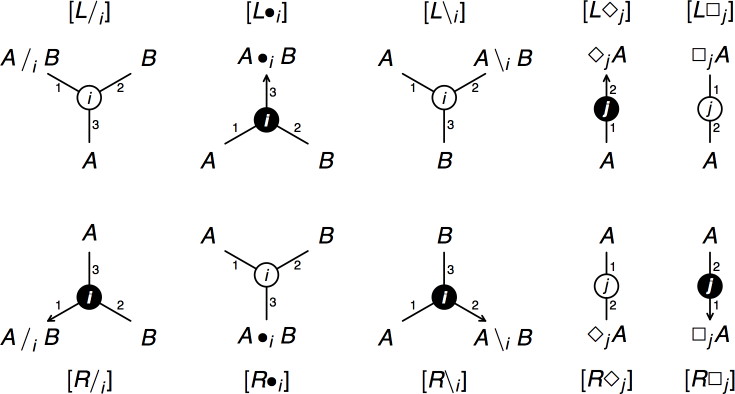
Figure 4. Links for NL grammars.
The new links are displayed with a filled circle at the centre, we will call them auxiliary links and distinguish them from the main links which have an open circle at the centre. For people familiar with linear logic: the main links correspond to tensor links and the auxiliary links correspond to par links. Unlike the main links, which have two hypotheses and a single conclusion, the auxiliary links have two conclusions and a single hypothesis. We distinguish between the left conclusion and the right conclusion of a link as we did for the two hypotheses of a main link.
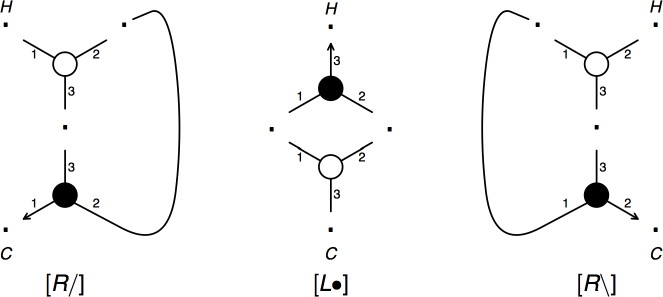
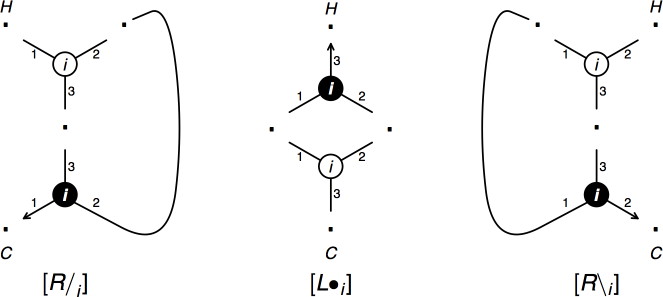
Figure 5. Contractions for NL grammars.
A contraction deletes one of the three subgraphs shown in Figure 5 and replaces it by a single vertex. All contractions are an instance of the same schema: a tensor link and a par link are connected by both paths not having the arrow (1 and 2 for the [L•] link, 1 and 3 for the [R\] link and 2 and 3 for the [R/] link).
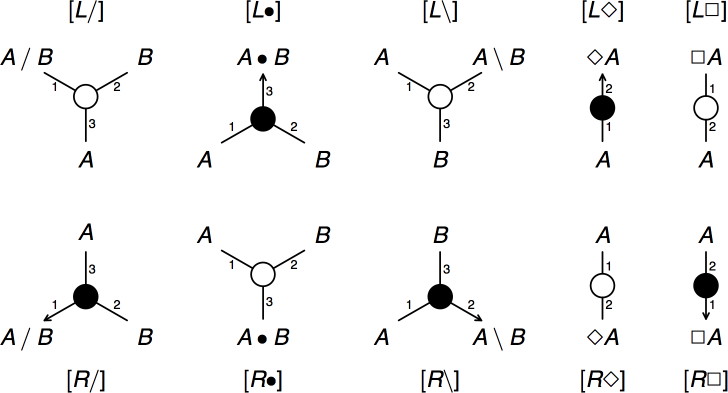
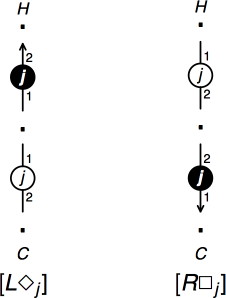
Figure 6. Links for NL◊ grammars.
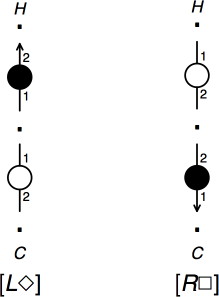
Figure 7. Unary Contractions.