Théorème de Penrose
Dans un article de 1997, Mathew Penrose caractérise le seuil minimal que doit avoir la portée de communication pour qu'un graphe géométrique aléatoire soit connexe presque à coup sûr. (Il formule le problème différemment, mais les conséquences sont les mêmes.)
Dans l'absolu, ce seuil dépendrait de la taille de la zone considérée ainsi que du nombre de noeuds qui s'y trouvent. Ici, Penrose considère que la zone est une surface de taille 1 x 1 (carré unitaire), ce qui permet de caractériser le seuil en fonction seulement du nombre de noeuds. Pour simplifier les calculs, il suppose (dans la variante de son résultat qui nous intéresse) que l'espace est toroidal.
Soit $r$ le seuil en question et $n$ le nombre de noeuds. Son théorème est souvent énoncé comme suit:
$$lim_{n \to \infty} (\pi r^2) = \frac{\ln n}{n}$$
Autrement dit, à mesure que $n$ devient grand, le seuil se rapproche de $r=\sqrt{\frac{\ln n}{\pi n}}\ $. Deux remarques concernant le résultat lui-même :
- Il existe bel et bien un effet de seuil, à savoir que si $r$ est juste en dessous du seuil, le graphe est quasi-certainement non-connexe; s'il dépasse cette valeur, il devient quasi-certainement connexe.
- Par contre, cela ne marche que pour des grandes valeurs de $n$ (d'où le fait que le résultat s'exprime comme une limite). Comme illustré sur la figure ci-dessous, la transition de phase est d'autant plus nette que $n$ est grand.
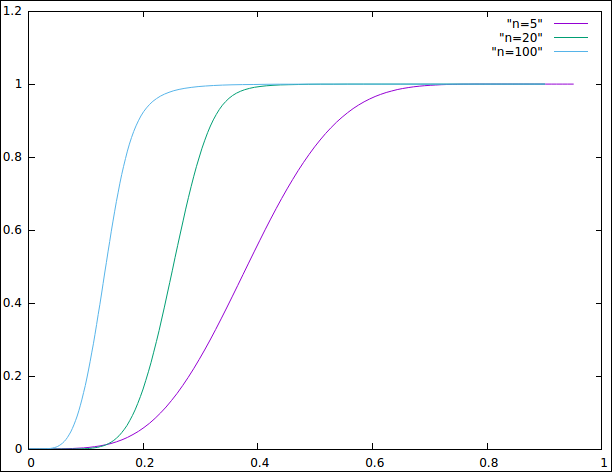
Probabilité de connexité en fonction de la portée
de communication (pour trois valeurs possibles de $n$).