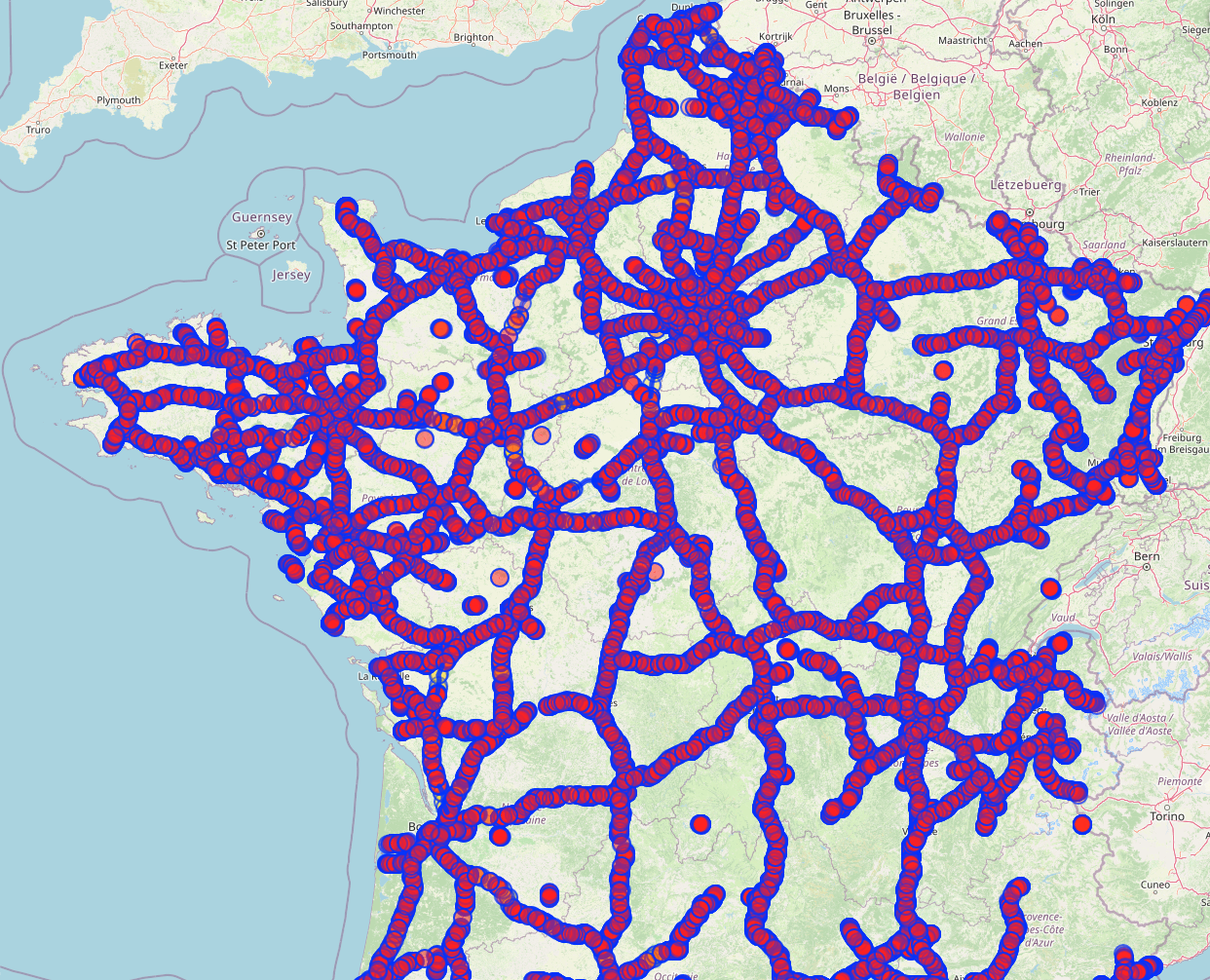
The European Parliament recently adopted a new rule on the placement of charging stations for electric cars on motorways. By 2026, all motorways will have to be equipped with at least one charging station every 60km.
To meet this requirement, it will be necessary to be able to give the location of the charging stations to be installed so that for every shortest freeway journey of at least 60km, there will be at least one charging station accessible. The aim is to minimize the number of stations installed.
The project will be carried out in several stages:
About the organization:
The problem is to place a minimum number of stations on the motorways. These stations will have to be placed in such a way as to satisfy certain constraints. Any path longer than 60km must be covered by a station. Charging stations can only be placed where the infrastructure allows, at rest areas and existing stations.
The input will therefore be the motorway network, the rest areas and the maximum number of km. The output will be a list of rest areas.
You will have to provide a visualization of the results including equipped freeways and stations.
To solve this problem, we suggest you use openstreetmap data. You can retrieve them in json format by writing queries to overpass-turbo.eu.
The following query retrieves freeways in France:
[out:json];
area[name = "France"];
(way(area)["highway"~"^(motorway|trunk)$"];>;);
out;

The highway=services and highway=rest_area correspond to existing service stations and rest areas. Refer to the openstreetmap wiki to retrieve other necessary information.
You will create instances of different sizes to be able to test even the slowest algorithms.
From this data, you will automatically build the problem instances.
This submission is optional (but recommended).
What is expected (by priority):
You have to provide a short report to explain your progress and your difficulties.
Annotated Dominant Set:
Based on the point 3 of the first submission, code a (polynomial) reduction of the problem to Dominating Set or Annotated Dominating Set. (What do you conclude about the complexity of the problem?)
For Dominating Set algorithms, you will make them possible to be called on graphs in text format. (.dot for example)
run example:
./my_program.py -SAT -g my_graph_20_vertices.dot -k 10Provide a report detailing the work carried out and any difficulties encountered. The report will examine both the theoretical and practical complexity (execution time) of the algorithms implemented.
The final submission is due no later than 01/12.
You will provide a report covering the following points:
You will describe in detail how to run your project on the CREMI machines, with examples. The project will be evaluated mainly on the report; anything not explained in the report will not be considered.
The defense will take place on 01/16 at CREMI (A28 room 203). They will last 20 to 25 minutes.
Here are the times for each group:
We ask you to enter the room discreetly 10 minutes before your scheduled time, and to settle in at a computer to avoid wasting time. You’ll need to give a brief presentation of what you’ve done, and then we’ll ask you questions about your project. You can use slides, but you don’t have to.