| Université BORDEAUX 1 |
U.F.R. Mathématiques et Informatique |
| Epreuve de J.Bétréma |
18 décembre 2006 |
Master Informatique 1ère année
INF 300 - Modèles de calcul
Durée: 3 heures
Tous documents interdits.
Un corrigé est disponible ci-dessous.
A tout ensemble d'entiers E,
de fonction caractéristique χ ,
on associe l'ensemble :
F = α ( E ) =
{ u0 ,
u1 ,
… ,
un ,
… }
où un désigne
l'entier dont la représentation binaire est la suivante :
le bit numéro n vaut 1,
et pour i < n,
le bit numéro i vaut
χ ( i ) ;
autrement dit :
un = 2n +
χ (0) + 2 χ (1) + 4 χ (2)
+ … +
2n-1 χ (n - 1)
- Exemple : on suppose que les premiers éléments
de E sont 2, 3, 5, …
Calculer les valeurs de u0 ,
u1 ,
… ,
u6 .
- Montrer que les entiers
un sont tous distincts.
Que peut-on en déduire pour F ?
- Montrer que si E est décidable,
F l'est aussi.
Note : on ne demande pas d'écrire les détails d'une
procédure C pour décider si
x ∈ F ,
il suffit d'écrire un algorithme clair et précis en langage libre.
- Montrer que si F est récursivement énumérable,
E est décidable.
Note : même recommandation
que pour la question précédente.
- Soit E un ensemble indécidable.
Montrer que F ne possède
aucun sous-ensemble F'
récursivement énumérable et infini.
- Donner plusieurs exemples d'ensembles indécidables.
Un corrigé est disponible ci-dessous.
On considère la machine de Turing M dont
l'alphabet ne contient que deux caractères
(le caractère blanc, désigné par un point ci-dessous,
et le caractère x)
et dont les règles sont les suivantes :
1 . 2 x Gauche
2 . 3 x Droite
3 . 1 x G
4 . 1 x G
1 x 1 x G
2 x 2 x D
3 x 4 x D
4 x 5 x D
5 x 3 . D
|
Dans la configuration initiale la bande est blanche,
et la machine M est dans l'état 1.
Il s'agit du "castor" à 5 états, mais son comportement
détaillé est sans importance pour cet exercice ;
on utilise seulement le résultat suivant :
pendant l'exécution, M écrit un mot u
sur la bande, et
la tête de lecture ne se déplace jamais à gauche de la
position -30 sur la bande (la position initiale est
la position 0).
|
Le but de l'exercice est de transformer
cette machine M en une machine
de Turing T
qui fonctionne comme M, mais en plus
compte le nombre d'instructions exécutées
par M. Pour cela on suppose que la bande
contient aussi la représentation binaire
d'un compteur, située suffisamment à gauche pour ne jamais
interférer avec les calculs de M ;
ce compteur est initialisé à 0,
et on dispose de règles qui permettent,
dans l'état numéro 10, et quelle que soit
la position de la tête de lecture à l'intérieur du mot u,
d'aller incrémenter le compteur, après quoi la machine
se trouve dans l'état 20, et la tête de lecture
juste à droite du compteur. Les états utilisés
pour cette opération d'incrémentation ont leurs
numéros compris entre 10 et 20.
Attention : les règles des machines
doivent être écrites et commentées très clairement ;
une réponse qui ne respecte pas cette consigne
risque de ne rapporter aucun point.
Ecrire les règles de T,
en ajoutant si nécessaire à l'alphabet initial
{ . x 0 1 }
des marqueurs bien choisis.
Note : il existe une solution simple avec une vingtaine de
règles, toutes sur le même modèle ;
inutile de les écrire toutes, il suffit d'en écrire une dizaine
pour montrer comment on les construit.
Attention : toute réponse qui,
pour incrémenter le compteur, utilise une autre méthode
que celle prédéfinie dans l'énoncé
(à savoir passer dans l'état 10, et attendre
que la machine se trouve dans l'état 20)
sera considérée comme nulle.
- Ecrire les instructions d'incrémentation
du compteur. Note : il existe une solution avec moins
de 10 règles, et un seul état (qu'on pourra numéroter 11)
autre que les états 10 (début d'incrémentation)
et 20 (fin d'incrémentation) ;
cette solution n'utilise aucun symbole en dehors de l'alphabet
{ . x 0 1 }.
Dans ces conditions
toute réponse trop compliquée sera considérée comme nulle.
- Comment résoudre la question 1 sans utiliser de marqueurs,
c'est-à-dire en se restreignant à l'alphabet
{ . x 0 1 } ?
On ne demande (surtout) pas d'écrire les règles détaillées
de la machine T, mais d'indiquer seulement
les grandes lignes d'une solution.
Un corrigé est disponible ci-dessous.
On considère une fonction calculable totale
f : N → N ,
et on lui associe la fonction g
définie par récurrence comme suit :
g (0) = 1 , et pour tout entier n :
g ( n + 1) =
f ( g ( n ) )
On suppose la fonction f
définie par un λ-terme F.
- Si f (n) = 2 n,
que vaut g ?
- Expliquer précisément ce que signifie :
" le λ-terme F définit la fonction
f " .
- Construire un λ-terme G
qui définisse g, en utilisant un opérateur
de point fixe Y
(on ne demande pas de définir
Y ).
- Même question que précédemment, mais sans utiliser
d'opérateur de point fixe.
Un corrigé est disponible ci-dessous.
On rappelle que le
problème 2-SAT est le suivant :
- Instance : une suite de clauses
(de taille 2)
ti ∨ tj ,
où ti désigne la variable booléenne
xi ou sa négation.
- Question : existe-t-il
un ensemble de valeurs,
pour les variables booléennes
x1 …
xn ,
qui donne la valeur 1 à toutes les clauses simultanément ?
A chaque instance de 2-SAT on associe un graphe
orienté G
construit comme suit :
- pour chaque variable booléenne
xi ,
G contient deux sommets notés
Ui et Vi ;
- pour chaque clause
xi ∨ xj ,
G contient un arc de
Vi vers Uj
et un arc de
Vj vers Ui ;
- pour chaque clause
¬ xi ∨ xj ,
G contient un arc de
Ui vers Uj
et un arc de
Vj vers Vi ;
- et ainsi de suite pour les deux autres cas
xi ∨ ¬ xj
et
¬ xi ∨ ¬ xj .
- Construire le graphe associé aux clauses :
¬ x ∨ y ,
¬ y ∨ z ,
x ∨ ¬ z ,
y ∨ z .
- Ecrire les implications
¬ x ⇒ y
et
¬ y ⇒ x
sous forme de clauses.
- Montrer que si G contient un chemin
de Ui vers Vi
(attention, ici c'est le même indice i ),
alors le système de clauses n'est pas satisfiable
si l'on choisit
xi = 1.
Que peut-on en déduire si G contient
à la fois un chemin de
Ui vers Vi
et un chemin de
Vi vers Ui ?
- On suppose qu'il n'existe pas d'indice i
tel que G contienne
à la fois un chemin de
Ui vers Vi
et un chemin de
Vi vers
Ui .
Montrer que dans ce cas le système de clauses est satisfiable.
Indication : s'il n'existe pas de chemin de
U1 vers
V1 ,
choisir x1 = 1,
puis traiter les sommets qu'on peut atteindre
à partir de
U1 .
- Existe-t-il un algorithme polynomial
pour décider si G possède la propriété énoncée
au début de la question précédente ?
- Que peut-on en déduire pour le problème 2-SAT ?
Corrigé.
Remarque sur le barème : les notes entre 10 et 32
ont été ajustées pour que la note finale soit comprise
entre 10 et 19.
Voir l'énoncé ci-dessus.
(Q1 + Q2 : 3 points). On a :
u0 = 1,
u1 = 2,
u2 = 4 car
χ (0) = χ (1) = 0,
u3 = 8 + 4 = 12 car
χ (2) = 1,
u4 = 16 + 4 + 8 = 28 car
χ (3) = 1,
u5 = 32 + 4 + 8 = 44 car
χ (4) = 0,
u6 = 64 + 4 + 8 + 32 = 108 car
χ (5) = 1 .
On peut remarquer la récurrence :
un+1 = un +
2n ( 1 + χ (n) ).
Certains étudiants se contentent de donner les réponses
en numération binaire, ce qui fait douter de leurs capacités
de calcul sur les puissances de 2.
- Le nombre de chiffres binaires de un
vaut exactement n + 1,
donc tous ces nombres sont distincts,
et forment un ensemble F infini.
(3 points). Dire que E est décidable signifie que sa
fonction caractéristique χ est calculable.
L'algorithme pour décider si
x ∈ F
peut alors s'énoncer ainsi :
écrire la représentation binaire de x ;
soit n le numéro du bit de poids le plus fort :
vérifier que pour tout
i < n
le bit numéro i est égal à
χ (i).
On peut écrire explicitement une procédure C,
mais l'énoncé ne le demandait pas :
/* fcE calcule la fonction caractéristique de E */
int fcE (int x) { … }
int fcF (int x) {
if (x == 0) return 0;
for (int i = 0; x > 1; i++) {
if ( x % 2 != fcE (i) ) return 0;
x = x / 2;
}
return 1;
}
Une variante un peu moins efficace mais
tout à fait raisonnable consiste à calculer
la suite des un
(qui est croissante)
jusqu'à trouver un élément de la suite
supérieur ou égal à x :
int fcF (int x) {
int u = 1, z = 1;
for (n = 0; u < x; n++) {
u = u + z * ( 1 + fcE (n) );
z = 2 * z;
}
return u == x;
}
(4 points).
Il faut cette fois donner un algorithme permettant de
décider si
n ∈ E.
Puisque F est récursivement énumérable et infini,
on peut énumérer ses éléments juqu'à trouver un
y supérieur à
2n+1, et retourner le chiffre binaire
numéro n de y !
Par exemple dès que 108 apparaît dans l'énumération de F,
on connaît les valeurs de la fonction caractéristique de E
jusqu'à n = 5 (cf question 1).
On peut écrire explicitement une procédure C,
mais l'énoncé ne le demandait vraiment pas :
/* f énumère F */
int f (int n) { … }
int fcE (int n) {
int i, y = f (0), z = 2;
for (i = 0; i < n; i++)
z = 2 * z;
for (i = 1; y < z; i++)
y = f (i);
for (i = 0; i < n; i++)
y = y / 2;
return y % 2;
}
- (3 points).
L'algorithme précédent fonctionne même si
l'image de la fonction d'énumération f
n'est pas F tout entier,
mais seulement un sous-ensemble F' infini.
Donc si E est indécidable,
on ne peut énumérer aucun sous-ensemble infini de F.
- (2 points). Question de cours.
Voir l'énoncé ci-dessus.
(4 points).
Avant d'exécuter une règle de M,
la machine T doit écrire une marque sur la bande,
puis passer dans l'état 10 ;
la marque doit identifier à la fois la position de la tête
de lecture, l'état de la machine M,
et le caractère présent sur la bande avant écriture de la marque.
Comme la machine M comporte neuf règles,
on utilise neuf marques
a, b, … i
et la première règle de M est remplacée par
deux règles :
// 1 . 2 x G (règle de M)
1 . 10 a G
20 a 2 x G
La seconde règle ci-dessus exprime qu'après
incrémentation du compteur (état 20),
lorsque la tête de lecture est revenue sur la marque a,
il faut exécuter la règle correspondante de M,
c'est-à-dire ici passer dans l'état 2, écrire un x,
et déplacer la tête de lecture vers la gauche.
Il faut aussi deux règles pour
déplacer la tête de lecture vers la droite
jusqu'à trouver une marque :
Voici les 20 règles de T qui remplacent
les 9 règles de M :
20 . 20 . D
20 x 20 x D
// 1 . 2 x G
1 . 10 a G
20 a 2 x G
// 2 . 3 x D
2 . 10 b G
20 b 3 x D
// 3 . 1 x G
3 . 10 c G
20 c 1 x G
|
// 4 . 1 x G
4 . 10 d G
20 d 1 x G
// 1 x 1 x G
1 x 10 e G
20 e 1 x G
// 2 x 2 x D
2 x 10 f G
20 f 2 x D
|
// 3 x 4 x D
3 x 10 g G
20 g 4 x D
// 4 x 5 x D
4 x 10 h G
20 h 5 x D
// 5 x 3 . D
5 x 10 i G
20 i 3 . D
|
Certain(e)s étudiant(e)s ont remarqué à juste titre
que les marqueurs c, d et e
jouent le même rôle, on peut donc remplacer
d et e par c,
et éliminer deux règles.
Note : chaque transition de M
est remplacée pendant l'exécution de T
par une suite de transitions, dont le nombre est voisin
de la distance entre le caractère courant de M
et le compteur, multipliée par deux.
Or la machine M écrit plusieurs milliers de caractères
sur la bande avant de s'arrêter,
donc le temps d'exécution de T vaut environ
dix mille fois celui de M ;
si on exécute T sur un simulateur,
il ne faut donc pas s'attendre à voir le programme
terminer rapidement…
(3 points). Pour incrémenter le compteur, dans l'état 10,
on déplace la tête de lecture à gauche jusqu'à trouver
un chiffre binaire ;
ensuite, de droite à gauche, on remplace chaque 1 par 0,
jusqu'à trouver un 0 ou un blanc, qu'on remplace par 1,
ce qui termine l'incrémentation.
Un nouvel état 11, différent de 10, est nécessaire
pour distinguer les caractères blancs
situés à droite du compteur
(lus sans modification dans l'état 10)
du caractère blanc situé
à gauche du compteur
(cas où le nombre à incrémenter ne comporte que des 1).
Une fois le compteur incrémenté (état 20),
il faut ramener la tête de lecture à droite du compteur,
en parcourant les 0 qu'on vient d'écrire.
Voici les huit instructions :
10 . 10 . G
10 x 10 x G
10 0 20 1 D
10 1 11 0 G
11 0 20 1 D
11 1 11 0 G
11 . 20 1 D
20 0 20 0 D
(3 points). Sans agrandir
l'alphabet { . x 0 1 },
on peut procéder comme suit : utiliser l'un des deux chiffres
binaires pour marquer la position de la tête de lecture
dans le mot u, et utiliser neuf états supplémentaires,
un par règle de M ; en numérotant ces états de 101
à 109, les règles de M sont donc remplacées par :
1 . 101 0 G
2 . 102 0 G
3 . 103 0 G
4 . 104 0 G
1 x 105 0 G
2 x 106 0 G
3 x 107 0 G
4 x 108 0 G
5 x 109 0 G
Ensuite, dans chacun de ces nouveaux états 101 à 109,
il faut écrire sur la bande
(par exemple juste à gauche du mot u)
quatre chiffres binaires qui codent l'un de ces neuf états
(des états annexes
supplémentaires sont nécessaires pour cette tâche) ;
ensuite on passe dans l'état 10 pour incrémenter le compteur ;
enfin dans l'état 20 on revient lire (et effacer) le code
écrit sur la bande pour passer dans l'un des états disons
201 à 209, puis on se déplace à droite
jusqu'à trouver un chiffre binaire, et enfin on exécute
la règle correspondante de M :
201 0 2 x G
202 0 3 x D
203 0 1 x G
204 0 1 x G
205 0 1 x G
206 0 2 x D
207 0 4 x D
208 0 5 x D
209 0 3 . D
Note : comme dans la question 1,
les états 203, 204 et 205
(et donc aussi les états 103, 104 et 105)
peuvent être confondus.
Une solution évidemment plus simple est d'utiliser neuf
(ou sept, selon la remarque précédente)
clones des instructions d'incrémentation du compteur,
pour ne pas oublier l'état initial pendant cette incrémentation ;
mais cette duplication de code n'est pas
recommandable en général. La solution proposée ci-dessus
est un analogue rudimentaire du fonctionnement
d'un processeur,
qui empile l'adresse de retour avant l'appel d'une procédure,
et dépile cette adresse après exécution de la procédure.
Voir l'énoncé ci-dessus.
(2 points). Si f (n) = 2 n,
on a :
g (0) = 1 ,
g (1) = 2 * g (0) = 2,
g (2) = 2 * g (1) = 4,
g (3) = 2 * g (2) = 8 …
et donc par récurrence
g (n) = 2 n ,
autrement dit g est la fonction exponentielle de base 2.
- (2 points). "Le λ-terme F définit la fonction
f " signifie que pour tout entier x,
le terme F x
se réduit en y, avec
y = f (x) ;
x et y désignent, comme d'habitude,
le codage des entiers x et y
en λ-calcul.
(3 points). On construit d'abord le terme suivant :
M = λ h n .
iszero n 1
( F ( h ( pred n ) ) )
de telle sorte que G est solution de
l'équation M G = G
(iszero désigne le terme qui code le test de nullité,
et pred celui qui code la fonction prédécesseur).
Par définition d'un opérateur de point fixe Y,
on a : G = Y M.
Réduisons par exemple G 3 :
G 3 = Y M 3
→
M G 3
→
iszero 3 1
( F ( G ( pred 3 ) ) )
→
F ( G 2 )
De même G 2 →
F ( G 1 ),
G 1 →
F ( G 0 ),
et enfin :
G 0
→
iszero 0 1
( F ( G ( pred 0 ) ) )
→
1
G 3
→ … →
F ( F ( F 1 ) )
(3 points). On reconnaît, à la fin de l'exemple ci-dessus,
le terme 3 F 1 ; de façon générale
il suffit d'appliquer l'opérateur n
à F et 1 :
G = λ n.
n F 1
Voir l'énoncé ci-dessus.
(Q1 + Q2 : 3 points).
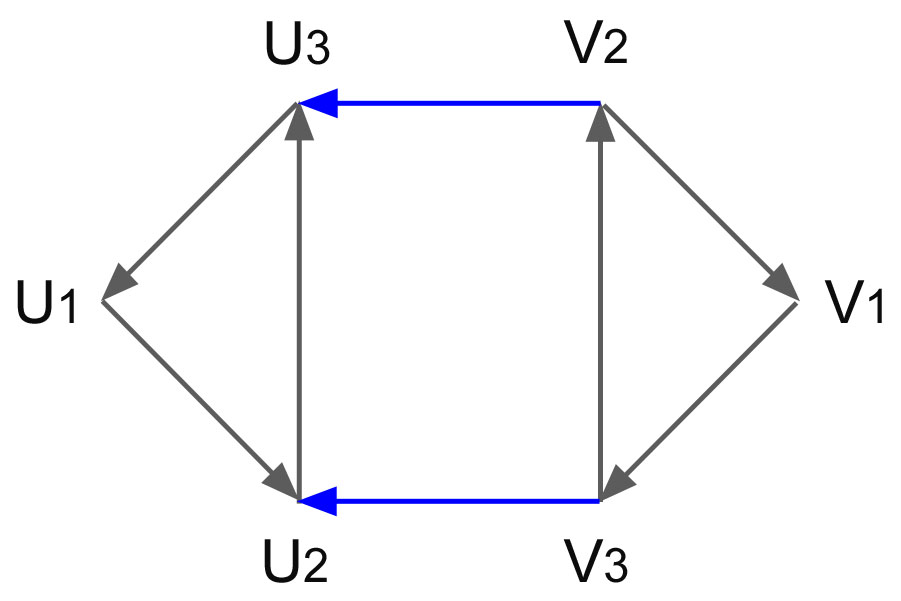
| En numérotant 1, 2 et 3 les variables x, y, z
on obtient le graphe ci-contre
associé aux clauses
¬ x ∨ y ,
¬ y ∨ z ,
x ∨ ¬ z ,
y ∨ z
(les arcs bleus correspondent à la dernière clause) :
|
|
Les implications
¬ x ⇒ y
et
¬ y ⇒ x
s'écrivent toutes les deux
x ∨ y
(la seconde implication est la contraposée de la première).
Suite aux deux premières questions,
on remarque donc que le graphe orienté G associé
à un ensemble de clauses de taille 2,
est le graphe des
implications équivalentes à ces clauses.
Sur l'exemple de la question 1, le triangle
U1 →
U2 →
U3 →
U1
peut se lire :
x ⇒ y ⇒ z ⇒ x
tandis que le triangle
V1 →
V3 →
V2 →
V1
correspond aux contraposées des implications précédentes :
¬x ⇒ ¬z ⇒ ¬y
⇒ ¬x
(3 points). Si G contient un chemin
de Ui vers Vi ,
le système de clauses comporte des clauses équivalentes
aux implications suivantes :
xi ⇒ t1
⇒ t2 ⇒ …
⇒ ¬xi
où t1 ,
t2 …
désignent des variables booléennes quelconques ou leurs négations.
Par transitivité de l'implication,
on en déduit que le système de clauses a pour conséquence :
xi ⇒
¬xi ,
autrement dit
¬xi
∨ ¬xi ,
soit tout simplement ¬xi ;
le système de clauses n'est donc pas satisfiable
si l'on choisit
xi = 1.
De même si G contient
un chemin de
Vi vers Ui ,
le système a pour conséquence xi ,
et n'est pas satisfiable
si l'on choisit
xi = 0.
S'il existe un indice i
tel que G contienne
à la fois un chemin de
Ui vers Vi
et un chemin de
Vi vers Ui ,
le système de clauses n'est pas satisfiable.
Note : la plupart des étudiant(e)s qui ont traité cette
question ont confondu chemin
(de Ui vers Vi )
et arc, ce qui n'est pas excusable ;
ils/elles ont donc affirmé que le système
contient la clause
¬xi
∨ ¬xi ,
ce qui est faux.
Cette question n'a pas été notée, car elle n'a jamais été
résolue correctement. En supposant par exemple
qu'il n'existe pas de chemin de
U1 vers
V1 ,
on choisit x1 = 1,
puis on traite tous les sommets qu'on peut atteindre
à partir de
U1 :
s'il existe un chemin de
U1 vers Ui
on pose xi = 1, et
s'il existe un chemin de
U1 vers Vi
on pose xi = 0.
Il faut alors montrer qu'on n'arrive jamais à une contradiction,
c'est-à-dire qu'il ne peut pas exister à la fois
un premier chemin de
U1 vers Ui
et un second chemin de
U1 vers Vi !
Pour cela on remarque que, par contraposition, le second chemin
implique l'existence d'un troisième chemin de
Ui vers V1 ;
par composition du premier et du troisième chemins,
on obtient un chemin de U1 vers
V1 , ce qui contredit l'hypothèse.
S'il reste des variables non traitées, on recommence
avec l'une d'entre elles, disons x2 ;
supposons cette fois qu'il existe un chemin de
U2 vers V2 ,
mais pas de chemin de
V2 vers U2 .
On pose x2 = 0,
puis on traite tous les sommets qu'on peut atteindre
à partir de V2 , comme ci-dessus.
Il faut à nouveau montrer l'absence de contradiction
avec la phase précédente
(traitement effectué à partir du choix
x1 = 1),
c'est-à-dire qu'il ne peut pas exister à la fois
un premier chemin de
U1 vers disons Vi
(d'où xi = 0)
et un second chemin de
V2 vers Ui
(d'où xi = 1).
L'argument est le même que ci-dessus : dans ce cas il
existerait un troisième chemin de
Vi vers U2
(par contraposition), d'où par composition un chemin de
U1 vers U2
qui contredit l'hypothèse selon laquelle la variable
x2 n'a pas été traitée dans la phase précédente.
D'accord, cette question était un peu difficile dans les conditions
d'un examen de 3h…
- (Q5 + Q6: 4 points).
Il existe un algorithme linéaire pour déterminer s'il existe
un chemin entre deux sommets A et B
d'un graphe (orienté ou pas) : on marque les sommets accessibles
directement à partir de A
(c'est-à-dire les extrémités des arcs de source A),
puis ceux accessibles à partir des sommets marqués,
et ainsi de suite. Pour vérifier la propriété de la question 4,
il faut répéter cet algorithme au plus 2n fois,
ce qui produit un algorithme quadratique, et donc polynomial.
On a construit une réduction polynomiale de 2-SAT
à un problème de chemins sur un graphe, qui appartient à P ;
on en déduit 2-SAT ∈ P.
Note : la réduction est bien polynomiale,
car la complexité de la construction du graphe est proportionnelle
au nombre de clauses.
