| Université BORDEAUX 1 |
U.F.R. Mathématiques et Informatique |
| Epreuve de J.Bétréma |
17 janvier 2005 |
Master Informatique 1ère année
INF 300 - Modèles de calcul
Durée: 3 heures
Tous documents interdits.
Un corrigé est disponible ci-dessous.
Dans cet exercice
(et dans le suivant), un semi-prédicat P
désigne une fonction booléenne
P : N → {0, 1},
qui peut être partielle.
Une procédure p calcule, comme d'habitude,
une fonction N → N.
- Soit E l'ensemble des procédures p
qui calculent des semi-prédicats. E est-il décidable ?
Note : la réponse doit être soigneusement justifiée ;
cette recommandation s'applique à toutes les questions,
et spécialement à celles où la
réponse demandée est "oui" ou "non".
- Soit F l'ensemble des procédures p
telles que chaque return soit suivi de 0 ou 1.
On suppose aussi que le texte de la procédure se termine par
une instruction return, pour garantir que le
résultat du calcul, si celui-ci termine,
est bien défini. F est-il décidable ?
- Montrer que tout semi-prédicat calculable P
peut être calculé par une procédure
p ∈ F.
Dans la suite, on associe
à tout semi-prédicat calculable P
l'ensemble suivant, appelé ensemble accepté
par P :
A ( P ) =
{ x | P (x) = 1 }
- A ( P ) est-il, en général, décidable ?
Note : si la réponse est "oui", il faut montrer que
A ( P )
est décidable pour tout semi-prédicat calculable P ;
si la réponse est "non", il faut montrer qu'il
existe des semi-prédicats calculables P tels que
A ( P )
ne soit pas décidable.
- A ( P ) est-il, en général,
récursivement énumérable ?
- Tout ensemble B
récursivement énumérable est-il de la forme
A ( P ) ?
On considère maintenant
les machines de Turing avec deux états
terminaux q0 et q1 .
La machine s'arrête lorsqu'elle atteint un état terminal,
et le résultat du calcul est 0 ou 1 selon l'état.
Si la machine boucle, ou si elle s'arrête dans un état non terminal
(par absence de règle applicable),
le résultat du calcul est indéfini.
On associe à toute machine M de ce type
l'ensemble suivant, appelé ensemble accepté
par M :
A ( M ) =
{ u | M (u) = 1 }
où M (u) désigne, comme d'habitude,
le résultat du calcul exécuté par M,
avec u écrit initialement sur la bande.
Un langage de la forme A ( M )
est dit reconnaissable par une machine de Turing.
- Que peut-on dire des langages
reconnaissables par des machines de Turing ?
Note : la réponse souhaitée est simple, technique,
et précise. Sinon, ne dites rien :
cela ne vous rapportera certes aucun point,
mais vous évitera, ici comme ailleurs, de perdre du temps
(et d'agacer le correcteur) !
Un corrigé est disponible ci-dessous.
A tout prédicat à deux variables
P ( x, y )
on peut associer une fonction f
définie par :
f ( x ) =
min { y | P ( x, y ) }
Idem si P est un semi-prédicat
(voir la définition au début de l'exercice 1,
à part cela les exercices sont indépendants),
mais dans ce cas, par exemple,
f ( x ) = 5
signifie :
P ( x, 5 )
∧ (
y < 5
⇒
¬ P ( x, y )
∨
P ( x, y )
non défini ).
- Ecrire (en langage C) une procédure qui calcule f
lorsque P est un prédicat calculable.
Dans quel cas l'exécution de cette procédure boucle-t-elle ?
Note : un prédicat, contrairement à un semi-prédicat,
est une fonction booléenne totale, c'est-à-dire toujours définie.
On souhaite écrire une procédure qui calcule f
même si P est un semi-prédicat (calculable).
On fait donc intervenir le temps, et après un peu de réflexion
on écrit la procédure suivante :
int phi (int x) {
for (t = 0; ; t++)
for (y = 0; y < t; y++)
if ( h (P, x, y, t) && P (x, y) )
return y;
}
où
h ( P, x, y, t )
exprime, comme d'habitude,
que le calcul de
P ( x, y )
est terminé au temps t.
Montrer que le calcul de
φ ( x )
termine si et seulement si
f ( x )
est défini. Montrer par contre que dans ce cas,
on peut avoir
φ ( x )
≠
f ( x ).
A votre avis, ce problème peut-il être corrigé ?
Si la réponse est positive, écrire une procédure correcte ;
si la réponse semble négative,
une preuve est, comme toujours, plus difficile ;
on demande seulement, dans ce cas, de donner en quelques lignes
des arguments en faveur de cette conjecture.
Soit
A ( x, q )
le semi-prédicat vrai si le calcul de
q ( x )
termine, et non défini sinon.
Ce semi-prédicat est-il calculable ?
Note : q désigne une procédure quelconque ;
on ne l'appelle pas p, pour éviter toute
confusion avec P.
- Montrer que, pour tout x, l'ensemble
{ q |
A ( x, q ) }
est infini.
On suppose que la fonction f associée
au semi-prédicat A est calculable ;
pour décider si le calcul de
q ( x )
termine, on compare q et
f ( x ) ;
si q <
f ( x ),
la réponse est facile, expliquer pourquoi ;
idem si
q =
f ( x ) ;
par contre si q >
f ( x ),
on n'est pas plus avancé.
Expliquer comment transformer A
pour obtenir un algorithme voisin du précédent
et qui résolve le problème de l'arrêt.
Que peut-on en conclure ?
Indication (partielle) : on peut ajouter une
troisième variable dans la définition de A.
A partir de maintenant
on revient à la situation de la question 1 :
P est un prédicat calculable.
On cherche à exprimer
f en λ-calcul. Pour cela,
on passe par la définition récursive suivante :
f ( x ) =
g ( x, 0 ) ;
g ( x, y ) =
si P ( x, y ) alors
y
sinon
g ( x, y + 1 )
- Vérifier que cette (curieuse) définition de f est correcte,
en expliquant en particulier pourquoi cette récurrence
"à l'envers" est valide.
- On suppose P défini par un λ-terme,
qu'on appellera aussi P.
En utilisant un opérateur de point fixe Y,
définir g par un λ-terme G.
Rappel : pour tout M,
Y M →
M ( Y M ) ;
on ne demande absolument pas de définir Y,
dont l'existence a été prouvée en cours ;
on demande de définir M tel que
G = Y M
réponde à la question posée.
- En utilisant G,
définir f par un λ-terme F.
On suppose que f (5) = 3 ;
réduire F 5.
Un corrigé est disponible ci-dessous.
Le problème de la coloration d'un graphe
avec 3 couleurs, appelé en abrégé 3-COL, est le suivant :
- Instance : un graphe G, non orienté,
avec m arêtes et n sommets.
- Question : les sommets de G
peuvent-ils être coloriés avec trois couleurs,
de telle sorte que deux sommets reliés par une arête
ne soient jamais de même couleur ?
Dans la suite, les couleurs seront notées
0, 1 et 2. Une coloration est donc une fonction
γ : S → {0, 1, 2},
où S désigne l'ensemble des sommets de G,
et où, pour toute arête
( i, j ),
on a :
γ ( i ) ≠
γ ( j ).
- Montrer soigneusement que 3-COL
appartient à la classe NP : expliquer en quoi consiste,
dans ce cas, un certificat,
et évaluer précisément la complexité de l'algorithme
de vérification du certificat.
A chaque sommet i on associe
trois variables booléennes
xi ,
yi et zi ;
la première (resp. seconde, troisième)
exprime que la couleur du sommet i
vaut 0 (resp. 1, 2).
Ainsi la clause :
xi ∨
yi ∨ zi
exprime que le sommet i est colorié.
Compléter ces n clauses pour obtenir un ensemble
de clauses Φ tel que tout choix de valeurs pour les
3 n
variables booléennes, qui satisfait Φ,
corresponde à une coloration de G,
et vice-versa.
- Combien de clauses la formule Φ contient-elle ?
La construction précédente constitue-t-elle une réduction
3-COL
→ SAT (ou plus précisément CNF),
ou l'inverse ? Cette réduction est-elle polynomiale ?
Note : on commencera par rappeler la définition
d'une réduction polynomiale
A → B,
où A et B désignent deux problèmes.
- La réduction précédente est en accord
avec un théorème fondamental, qu'on demande d'énoncer.
Dans la suite on part, inversement,
d'un ensemble Φ de clauses, auquel on veut associer
une instance de
3-COL.
Pour cela on construit un graphe comme suit :
- A chaque variable booléenne xi
on associe un segment
Ui Vi
(c'est-à-dire deux sommets, qu'on appellera principaux,
reliés par une arête).
- A chaque opérateur ∨ on associe
un triangle Aj
Bj
Cj
(c'est-à-dire trois sommets, qu'on appellera annexes,
reliés par trois arêtes).
Aj est appelé tête du triangle.
- Si, par exemple, la première clause débute par
x1
∨
¬ x2 ,
on relie par une arête
le sommet principal
U1
au sommet annexe B1 ,
et le sommet principal
V2
au sommet annexe C1 .
-
Si, par exemple, la première clause débute par
x1
∨
¬ x2
∨
x3 ,
on la traite comme
( x1
∨
¬ x2 )
∨
x3 :
U1 et V2
sont attachés au premier triangle comme ci-dessus,
puis on relie
sa tête A1
à B2 ,
et U3
à C2 .
Et ainsi de suite : une clause comportant k
variables est représentée par une chaîne de
k - 1
triangles ; la seule tête de triangle qui reste "libre"
est appelée tête de clause.
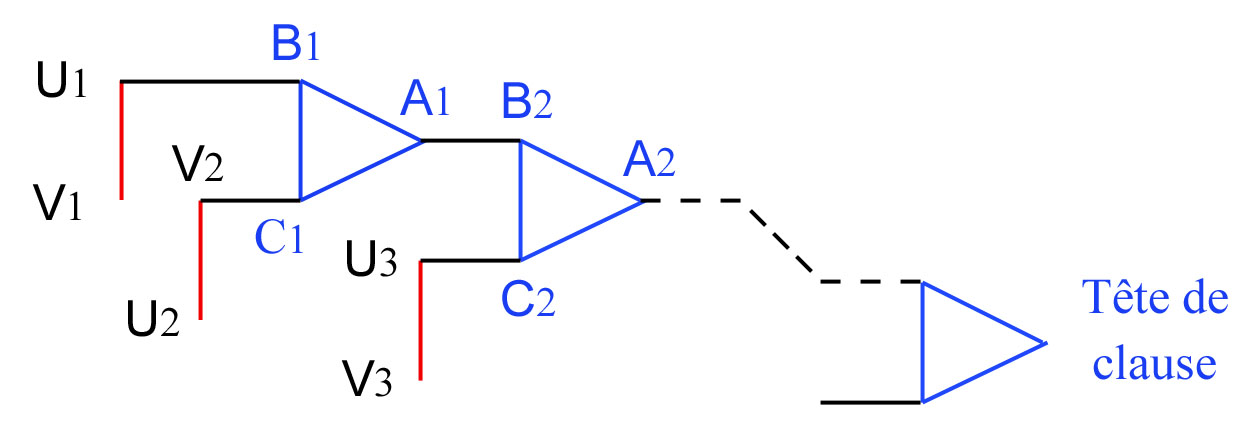
Le graphe G comporte enfin
deux sommets supplémentaires, notés Z (zéro)
et N (neutre), et reliés entre eux.
Z a pour couleur 0, et N
a pour couleur 2 : en permutant les couleurs,
on peut toujours adopter cette convention,
qui n'est donc pas restrictive.
N est relié à tous les
sommets principaux et à toutes les têtes de triangles ;
Z est relié à toutes les têtes de clauses.
Questions :
- Compléter le dessin pour le graphe associé aux clauses
( x1
∨
¬ x2
∨
x3
∨
x4 )
et
( ¬ x1
∨
x2
∨
x4 ).
Ce graphe comporte 5 triangles ;
ne pas dessiner les sommets N et Z,
ni les arêtes issues de ces sommets.
- Expliquer le rôle des sommets N et Z.
- Montrer que si une tête de triangle Aj
a pour couleur 1,
au moins l'un des sommets
— autres que Aj —
reliés à Bj et Cj ,
a pour couleur 1.
- Illustrer, sur l'exemple de la question 5, comment
tout choix de valeurs pour les 4
variables booléennes, qui satisfait les deux clauses,
correspond à une coloration de G,
et vice-versa.
- Evaluer précisément, en fonction du nombre n'
de variables booléennes et du nombre m' de connecteurs ∨ ,
la taille du graphe ainsi construit.
En déduire que cette construction
est une réduction polynomiale
… → …
(compléter).
- En déduire que 3-COL
est NP-complet, en donnant les détails
de la (courte) preuve.
Corrigé.
Remarque sur le barème : les notes entre 10 et 30
ont été ajustées pour que la note finale soit comprise
entre 10 et 18. La copie qui a obtenu 51 points a laissé
le correcteur perplexe…
Voir l'énoncé ci-dessus.
(3 points).
Non, E n'est pas décidable, à cause du théorème
de Rice. E est défini par une propriété
qui ne dépend
que de la fonction calculée par p,
à savoir :
∀x .
p (x)
= 0 ou 1 (ou n'est pas défini).
Cette propriété n'est pas triviale
(elle n'est ni toujours vraie ni toujours fausse),
donc le théorème de Rice s'applique.
Note : pour obtenir les 3 points, il faut
énoncer correctement le théorème de Rice.
- (2 points). Oui, F est décidable, car au contraire
F est défini par une propriété du texte
de la procédure p, qui peut être vérifiée
automatiquement par un analyseur syntaxique.
(1 point). Soit q une procédure qui calcule P ;
par définition,
q ∈ E,
mais il est très
facile de transformer q en une procédure
p ∈ F :
int p (int x) {
if (q (x) == 0) return 0;
[else] return 1;
}
Si q ∈ E, p et q
calculent la même fonction, et réciproquement.
Note : c'est exactement la convention du langage C,
qui ne possède pas de type booléeen,
et définit "vrai" par "différent de 0".
-
Barème : 4 points pour l'ensemble
des questions 4, 5 et 6.
Non, en général A ( P )
n'est pas décidable, voir pourquoi ci-dessous
(question 6).
Note : certain(e)s étudiant(e)s ont traité une question
différente, avec des contorsions diverses pour essayer
de (se) le cacher. Ils/elles ont démontré que l'ensemble
{ ( P , x ) | P (x) = 1 }
est indécidable, en adaptant la preuve de l'indécidabilité
du problème de l'arrêt, ou en invoquant directement le théorème
de Rice. Ce n'était pas la question posée,
d'ailleurs il est évidemment faux que
A ( P )
ne soit jamais décidable.
Oui, A ( P )
est récursivement énumérable, car semi-décidable.
En effet la fonction semi-caractéristique de cet ensemble
est peu différente de P, et
peut être calculée par la procédure suivante :
int scA (int x) {
int y = p (x);
if (y == 1)
return 1;
while (1);
}
où p désigne une procédure qui calcule P ;
scA (x)
vaut 1 si x ∈ A ( P ).
Sinon, ou bien P n'est pas défini, et le calcul de y
ne termine pas ; ou bien
P (x) = 0,
et l'instruction while(1)
ne termine pas.
Note : beaucoup d'étudiant(e)s ont
confondu la définition de
A ( P )
et celle d'un ensemble semi-décidable ;
la différence est légère, mais P
n'est pas exactement la fonction semi-caractéristique de
A ( P ),
car P peut prendre la valeur 0,
contrairement à une fonction semi-caractéristique.
Oui, tout ensemble B récursivement énumérable
est de la forme
A ( P ),
car B est semi-décidable,
donc il suffit de choisir pour P la fonction
semi-caractéristique de B.
Ceci justifie la réponse donnée à la question 4,
car il existe des ensembles récursivement énumérables
et non décidables.
- (2 points). On sait que les machines de Turing ont exactement
la même puissance de calcul que les procédures d'un modèle
de programmation impératif, comme C.
Donc les langages reconnaissables par des machines de Turing
sont exactement les langages de la forme
A ( P ),
c'est-à-dire les langages récursivement énumérables.
Rappel : un mot sur un alphabet de taille b,
peut être considéré comme la représentation d'un entier
en base b ; il n'y a donc pas de différence
entre un langage et un ensemble d'entiers.
Voir l'énoncé ci-dessus.
(2 points) Procédure de calcul de f :
int f (int x) {
for (int y = 0; ! P (x, y); y++);
return y;
}
Le calcul de f ( x )
boucle lorsqu'il n'existe pas d'entier
y tel que
P ( x, y ).
Note. Si P est un semi-prédicat,
il y a un second cas où le calcul ne termine pas :
(*) ∃y .
P ( x, y ) non défini
∧
( z < y ⇒
¬
P ( x, z ) )
En théorie de la calculabilité,
l'opérateur de minimisation,
qui transforme le semi-prédicat P en
une fonction notée μP :
μP ( x ) =
"min" { y | P ( x, y ) }
respecte la convention ci-dessus : lorsque la condition (*)
est vérifiée,
μP ( x )
n'est pas défini. Ainsi μ transforme une fonction
booléenne calculable partielle en une fonction
elle aussi calculable partielle.
La définition de f donnée dans l'énoncé
est la définition mathématique standard du minimum
d'un ensemble, mais
les questions suivantes
montrent que f n'est en général pas calculable,
lorsque P est un semi-prédicat calculable.
Inversement μP
ne calcule pas un vrai minimum, d'où les guillemets
autour de "min".
(2 points) Avec les conventions de l'énoncé,
f ( x ) est défini dès que l'ensemble
E =
{ y |
P ( x, y ) }
n'est pas vide.
- Si le calcul de y =
φ ( x )
termine, cet entier y vérifie
P ( x, y ),
et donc E n'est pas vide.
- Réciproquement, si E n'est pas vide,
soit y0 un élément de E :
il existe t0 tel que le calcul de
P ( x, y0 )
est terminé au temps t0 .
Le calcul de
φ ( x )
ne peut pas boucler, car
dès que t dépasse à la fois t0
et y0,
la condition qui suit if
est vérifiée pendant l'exécution de la boucle interne.
(2 points) Par contre
φ ( x )
est l'entier
y ∈ E
dont le calcul est le plus rapide, et non le minimum
de E.
(1 point) Ce problème ne semble pas pouvoir être corrigé,
car on voit bien comment transformer la procédure
phi pour énumérer tous les éléments
de E, mais comment savoir, pendant cette
énumération, à quel instant apparaît l'élément minimal ?
Si 5 est le minimum des
éléments énumérés après plusieurs jours de calcul,
comment savoir si, en attendant quelques instants de plus,
on ne va pas voir apparaître 2 ?
(2 points) Oui, A est calculable,
car c'est la fonction semi-caractéristique de l'ensemble :
H =
{ ( q, x ) | q ( x ) termine }
qui est récursivement énumérable, donc semi-décidable.
- (2 points) Pour tout x, il existe une infinité de procédures
q telles que le calcul de
q ( x )
termine ; par exemple
"return x",
"return x + 1",
"return x + 2", etc. ;
les procédures
"return 0",
"return 1",
"return 2", etc. ,
qui ne tiennent pas compte de leur argument x,
conviennent aussi.
(2 points) f ( x ) est (le numéro de)
la première procédure p
(dans l'ordre de numérotation des procédures)
telle que le calcul de
p ( x )
termine ; d'après la question précédente,
f ( x )
est toujours défini.
Si q <
f ( x ),
on est sûr que le calcul de
q ( x )
ne termine pas.
Si q =
f ( x ),
on est sûr que le calcul de
q ( x )
termine.
(3 points) Soit
B ( x, n, q ) =
n ≤ q ∧
A ( x, q ).
On peut considérer les deux premiers arguments de B
comme un couple
( x, n ) ;
si la fonction
g ( x, n )
associée à B :
g ( x, n ) =
min { q | B ( x, n, q ) }
était calculable,
il suffirait de comparer, comme ci-dessus,
q et
g ( x, q )
pour savoir si le calcul de
q ( x )
termine.
On en conclut que la fonction f définie au début
de cet exercice n'est en général pas calculable,
lorsque P est un semi-prédicat calculable.
Au lieu d'utiliser explicitement H, on peut
raccourcir l'argument en considérant n'importe quel ensemble
infini E récursivement énumérable
et non décidable. On définit :
P ( x, y ) =
x ≤ y ∧ y ∈ E
On a :
x ∈ E
⇔
f ( x ) = x,
et f est totale, car E est infini.
Si la fonction f était calculable,
E serait décidable.
(2 points) Si f ( x ) est défini,
et vaut par exemple 5, on a :
f ( x ) =
g ( x, 0 ) =
g ( x, 1 ), car
P ( x, 0 ) est faux ;
g ( x, 1 ) =
g ( x, 2 ), car
P ( x, 1 ) est faux ; etc. jusqu'à
g ( x, 5 ) = 5, car
P ( x, 5 ) est vrai.
Si f ( x ) n'est pas défini,
le calcul récurrent ne termine pas, puisque
∀y .
¬ P ( x, y ).
(3 points) Soit M = λ g x y .
if ( P x y )
y ( g x ( succ y )).
Alors G = Y M
vérifie, quels que soient les entiers
m et n :
G m n
→
M G m n
→
if ( P m n )
n ( G m ( succ n ) ) .
(2 points) F = λ x .
G x 0 , et si f (5) = 3, on a :
F 5
→
G 5 0
→
if ( P 5 0 )
0 ( G 5 ( succ 0 ) )
→
→
if false 0
( G 5 ( succ 0 ) )
→
G 5 ( succ 0 )
→
G 5 1
De même :
G 5 1
→
G 5 2
→
G 5 3
Enfin :
G 5 3
→
if ( P 5 3 )
3 ( G 5 ( succ 3 ) )
→
if true 3
( G 5 ( succ 3 ) )
→
3 .
Voir l'énoncé ci-dessus.
- (2 points) 3-COL
appartient à la classe NP,
car un certificat est une coloration γ,
et le vérifieur doit simplement s'assurer
que, pour chaque sommet i,
γ ( i )
est compris entre 0 et 2,
et que chaque arête a ses extrémités de couleurs
différentes. La complexité de cette vérification
est donc proportionnelle à
m + n.
(3 points) Pour chaque arête ( i, j ),
il faut ajouter les trois clauses suivantes :
¬ ( xi ∧ xj )
=
¬xi ∨ ¬xj
,
¬yi ∨ ¬yj
,
¬zi ∨ ¬zj
Remarque : il est inutile (mais pas faux) d'ajouter
des clauses pour exprimer qu'un sommet ne possède
pas simultanément plusieurs couleurs ;
en effet autoriser deux couleurs pour un sommet i
rend la coloration du graphe plus difficile :
il ne reste plus de choix pour la couleur
des sommets reliés à i.
Autrement dit, si Φ est satisfaite
avec par exemple
xi = yi = 1,
Φ est aussi satisfaite
avec xi = 1 et
yi = 0.
(3 points) Φ comporte 3 m + n clauses.
La construction précédente constitue une réduction f :
A = 3-COL
→
B = SAT
(et même
B = 3-CNF).
En effet à chaque instance G du problème A,
on a associé une instance Φ =
f ( G )
du problème B,
de telle sorte que
A ( G )
— autrement dit "G est 3-coloriable",
soit équivalent à
B ( Φ )
— autrement dit "Φ =
f ( G )
est satisfiable".
Décrire la construction f comme un
algorithme détaillé, avec les structures de données
adéquates, serait certainement assez long et délicat ;
on peut cependant affirmer sans risque
que la complexité de cet algorithme est polynomiale,
car la taille de Φ
est une fonction linéaire de la taille de G.
- (2 points) La réduction précédente est en accord
avec le théorème de Cook,
qui dit que SAT est NP-complet :
pour tout problème A de la classe NP,
il existe une réduction polynomiale
A → SAT.
(2 points) Voici le graphe associé aux clauses
( x1
∨
¬ x2
∨
x3
∨
x4 )
et
( ¬ x1
∨
x2
∨
x4 ) :
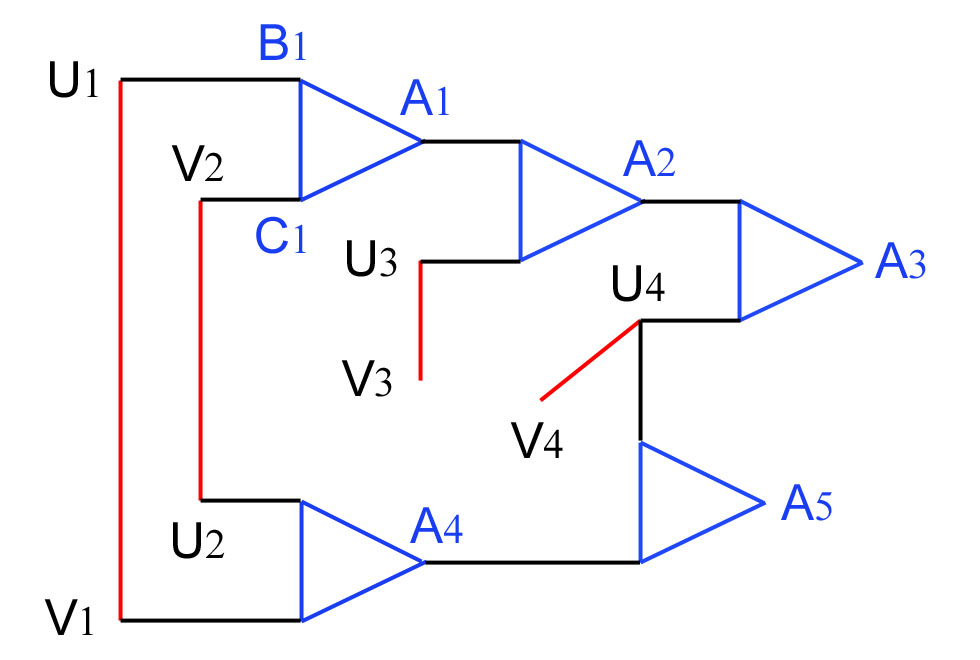
Les sommets V3 et V4
ne sont reliés à aucun triangle, car
¬x3 et
¬x4 n'apparaissent
dans aucune clause.
Au contraire le sommet U4
est relié à deux triangles, car
x4 apparaît dans deux clauses.
Le sommet N n'apparaît pas sur le dessin,
mais est relié à tous les sommets
Ui ,
Vi et
Aj .
Le sommet Z n'apparaît pas sur le dessin,
mais est relié aux sommets
A3 et A5 .
- (2 points) Le sommet N force tous les sommets principaux
et toutes les têtes de triangles à être coloriés 0 ou 1 ;
Z force la couleur des têtes de clauses à 1.
- (2 points) Si une tête de triangle A
a pour couleur 1, l'un des sommets
B ou C
a pour couleur 0 ;
supposons que ce soit B.
Le sommet relié à B est un sommet principal
ou une tête de triangle, donc n'est pas colorié 2
(car il est relié à N, voir question précédente) ;
la seule couleur restante est 1.
(3 points) Choisissons par exemple
x1 = 0,
x2 = 1,
x3 = 1,
x4 = 0.
La coloration correspondante du graphe
attribue la couleur 0 aux sommets
U1 ,
V2 ,
V3 et
U4 ;
les autres sommets principaux, soit
V1 ,
U2 ,
U3 et
V4 reçoivent la couleur 1.
La seule couleur possible pour
A1 est 0
(voir question précédente), tandis que
B1 et
C1 sont coloriés 1 et 2.
Par contre, grâce à U3
qui est colorié 1,
on peut attribuer la couleur 1 au sommet
A2 ;
le sommet relié à U3
est colorié 0, et le troisième sommet du
triangle est colorié 2.
Ceci correspond au fait que la valeur
x3 = 1
satisfait la première clause.
Enfin A3
est colorié 1 (pas d'autre choix, car c'est une
tête de clause, reliée à Z),
et le sommet entre A2 et
A3 est colorié 0.
Et ainsi de suite, voir dessin :
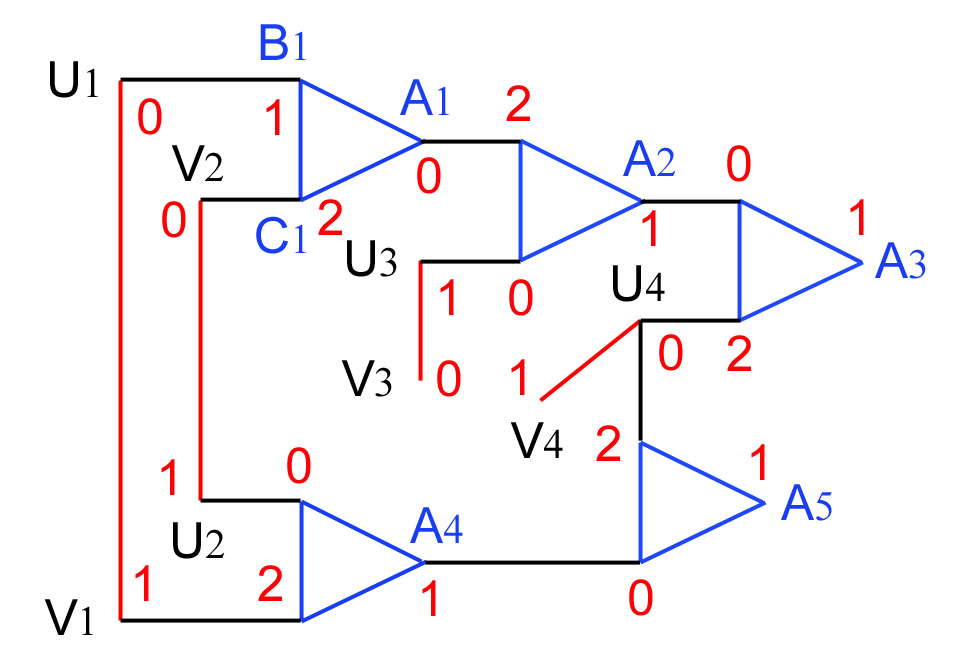
Inversement, à partir d'une coloration,
on attribue la valeur 0 (respectivement 1)
à la variable xi
si le sommet Ui est colorié 0
(respectivement 1).
Comme une tête de clause est de couleur 1
(car reliée à Z, voir question 6),
l'un des sommets principaux reliés aux triangles
qui composent cette clause, est lui-même colorié 1
(voir question précédente) ;
donc chaque clause est satisfaite.
(2 points) Le graphe comporte 2 n'
sommets principaux, et m' triangles,
donc le nombre de sommets vaut :
n =
2 n' + 3 m' + 2 .
Les arêtes se classent comme suit :
- n' arêtes rouges qui relient les
sommets principaux Ui
et Vi ;
- 3 m' arêtes bleues formant les triangles,
et 2 m' arêtes noires issues des sommets
Bj et Cj ;
- 2 n' + m' arêtes issues de N ;
- c + 1 arêtes issues de Z, où c
désigne le nombre de clauses, qui est inférieur à m'.
D'où le nombre d'arêtes :
m = n'
+ 3 m' + 2 m'
+ 2 n' + m' + c + 1
= 3 n' + 6 m' + c + 1 .
Comme on l'a indiqué question 3,
décrire la construction g,
qui transforme un ensemble de clauses en un graphe,
comme un algorithme détaillé, avec les structures de données
adéquates, serait certainement long ;
on peut cependant affirmer sans risque
que la complexité de cet algorithme est polynomiale,
car la taille de G
est une fonction linéaire de la taille de Φ.
La construction g est une réduction polynomiale
CNF → 3-COL.
En effet à chaque instance Φ de CNF,
c'est-à-dire à chaque ensemble de clauses Φ,
on a associé une instance G =
g ( Φ )
du problème 3-COL,
de telle sorte que:
Φ est satisfiable
⇔
g ( Φ ) est 3-coloriable.
- (2 points) On en déduit que 3-COL
est NP-complet.
En effet tout problème
dans la classe NP peut être réduit
polynomialement à SAT (théorème de Cook) ;
on peut réduire polynomialement SAT à CNF,
et CNF à 3-COL (question précédente).
Donc tout problème
dans la classe NP peut être réduit
polynomialement à 3-COL.


