Théorème de Church-Rosser. Si le terme M peut être réduit en M1 d'une part, et en M2 d'autre part, alors il existe un terme N tel qu'on puisse réduire à la fois M1 et M2 en N.
| Chapitre 5 : Machines de Turing | Table des matières | Chapitre 7 : Complexité descriptive |
| Exercices |
Le λ-calcul fournit d'abord une notation pour transformer une expression (par exemple 2 x + 1 ) en une fonction :
F = λ x . 2 x + 1
désigne la fonction notée traditionnellement x → 2 x + 1 ; cette construction est appelée abstraction.
Cette λ-expression comporte deux parties, séparées par un point : à gauche figure une variable, dite liée, à droite on a le corps de F. Le nom de la variable liée est sans importance, l'expression λ t . 2 t + 1 est équivalente ; en λ-jargon, le changement de nom d'une variable liée est appelé α-conversion.
Pour appliquer F à un argument (par exemple a2 + b2 ), on substitue, dans le corps de F, l'argument à la variable liée, ce qui donne ici : 2 ( a2 + b2 ) + 1 ; cette opération de substitution est appelée β-réduction.
L'usage est de noter, par simple juxtaposition, F M l'application de F à l'argument M ; cette convention diffère en deux points de la convention mathématique usuelle :
les lettres minuscules sont réservées aux variables, une majuscule désigne donc une expression quelconque ; cette convention, adoptée dans ce cours, n'est pas universelle (autrement dit elle n'est pas utilisée dans tous les traités de λ-calcul), contrairement à la précédente.
Les parenthèses sont utilisées comme d'habitude pour lever les ambiguïtés. Une fonction de deux variables est représentée comme sur l'exemple suivant :
G = λ x . ( λ y . x2 + y2 )
autrement dit comme la fonctionnelle qui, à une variable x, associe la fonction d'une variable y : élever y au carré et ajouter x2. Cette représentation d'une fonction de plusieurs variables par des fonctions d'une variable emboîtées est désignée par le terme barbare de curryfication (sic), fabriqué à partir du nom du mathématicien Haskell Brooks Curry. On abrège l'expression ci-dessus en :
G = λ x y . x2 + y2
De même on note par simple juxtaposition l'application de G à deux arguments M et N, ce qui revient (on le vérifiera) à la convention suivante :
G M N est une abréviation pour : ( G M ) N
Dernière convention d'allègement des parenthèses : le corps d'une abstraction est implicitement parenthésé, autrement dit λ x . M N désigne toujours λ x . ( M N ), et non ( λ x . M ) N — dans ce dernier cas, il faut garder les parenthèses.
Pour exposer les notations du λ-calcul, dans la section précédente, nous avons utilisé des expressions arithmétiques, comme 2 x + 1 ou x2 + y2. Le λ-calcul pur ne suppose définis ni les entiers, ni a fortiori les opérations arithmétiques ; une λ-expression est construite récursivement à partir des variables, et des seules opérations d'abstraction et d'application. Autrement dit :
Il n'y a pas d'autre règle de construction d'une λ-expression — en dehors du parenthésage pour lever les ambiguïtés. Dans la suite de ce chapitre nous appellerons terme une λ-expression quelconque ; une variable est donc un terme, mais un terme n'est pas, en général, une simple variable. Un terme peut être représenté par son arbre : les feuilles sont étiquetées par des variables, et les noeuds internes sont étiquetés par λ (dans le cas d'une abstraction) ou ne sont pas étiquetés (dans le cas d'une application).
En λ-calcul, on emploie indifféremment les mots terme, λ-terme, expression et λ-expression, qui tous désignent le même objet. Dans ce chapitre, nous respecterons une convention fréquente en λ-calcul : les lettres minuscules désignent des variables, tandis que les majuscules désignent des termes. Les variables f ou g (respectivement F ou G ) sont des variables (resp. des termes) comme les autres, ces symboles facilitent simplement, pour les pauvres humains, la lecture et l'interprétation des expressions ; mais en λ-calcul il n'y a pas de classes distinctes de variables pour représenter des fonctions, et tout terme M peut être considéré à la fois comme une fonction (par exemple dans l'expression M N ), ou comme un argument (par exemple dans l'expression N M ). Rappelons aussi les conventions suivantes :
Un terme est un programme, qu'on "exécute" par (β-)réductions successives :
( λ x . M ) N → M [ N / x ]
où M [ N / x ] désigne le résultat du remplacement (substitution), dans le terme M, de la variable x par le terme N (attention, cette notation ne désigne pas une nouvelle opération primitive de construction de termes, elle désigne une transformation de termes). Le terme de gauche, dans la définition ci-dessus, c'est-à-dire le terme avant réduction, est appelé traditionnellement un redex ; son arbre est caractérisé par une racine sans étiquette (application), dont le fils gauche est étiqueté λ (abstraction).
Des changements de noms de variables liées ( α-conversions, en λ-jargon) sont parfois indispensables avant d'effectuer une substitution (et donc une β-réduction) ; la définition rigoureuse d'une substitution est, dans ces conditions, assez pénible, et se trouve dans tout cours classique de λ-calcul. Voir par exemple le document de Paulson, sections 1.2 (Variable Binding and Substitution) et 1.3 (Avoiding Variable Capture in Substitution) ; ou le cours de Goubault-Larrecq, section 1.2 (Calculs et réductions). Nous ne donnerons pas les détails : tant qu'on n'écrit pas un compilateur de λ-calcul, on peut se contenter de renommer "intelligemment" les variables en cas de danger, on le verra dans certains des exemples qui suivent.
Ce modèle de calcul, par récritures, se révèle équivalent à celui des machines de Turing, aussi étonnant que cela puisse paraître. Le λ-calcul est à la base de nombreux langages de programmation, dits fonctionnels, tels que Lisp (dont il existe plusieurs dialectes), Scheme, ou ML et sa variante CaML. Le λ-calcul pur est à ces langages ce que la machine de Turing est au langage C. Il faut commencer par définir les entiers et les opérations arithmétiques, ce qui semble un défi avec les faibles moyens dont nous disposons.
Les entiers de Church sont des opérateurs sur les fonctions : par exemple 3 est l'opérateur λ f . f 3, où f 3 est une abréviation pour λx . f ( f ( f x ) ). D'où les définitions :
Note : I = λ f . f = λ x . x est aussi un bon candidat pour définir 1. Ce ne sont pourtant pas les mêmes termes, et ils ne se réduisent pas l'un à l'autre : ils sont tous deux irréductibles, autrement dit ne contiennent aucun redex. L'entier 1 vaut λ f . ( λ x . f x ), et savoir si l'on peut remplacer, entre les parenthèses, λ x . f x par f, revient à savoir si plus généralement on peut remplacer F = λ x . M x par M, lorsque x n'est pas libre dans M. Cette tranformation est appelée, en λ-jargon, une η-conversion, et traduit le principe d'extensionalité (un seul 'n', si, si, comme dans rationalité) : pour tout terme U, F U → M U ; autrement dit F et M sont équivalents dès qu'on les applique à un argument. Ce principe n'est pas essentiel au λ-calcul, et on peut s'en dispenser.
Tout entier de Church n est donc un opérateur qui transforme f en f n ; cette notation f n, usuelle en mathématiques pour désigner f ο f ο … ο f, est donc remplacée en λ-calcul par n f. On définit alors les opérateurs succ (successeur), add (addition), mul (multiplication), exp (exponentielle) par :
Attention : comme la multiplication est commutative, l'ordre de m et n dans le corps de mul est sans importance ; par contre il est essentiel pour le calcul de m n ! D'autre part, on a réduit au maximum le parenthésage des termes ci-dessus, selon les conventions de la fin de la section 1 ; par exemple n f ( f x ) doit être interprété comme ( n f ) ( f x ) ; oublier les parenthèses autour de "f x" serait par contre une faute, car n f f x désigne ( n f f ) x.
Note : le λ-calcul pur n'est pas typé : rien n'indique, dans la définition des opérateurs ci-dessus, que m ou n sont des entiers ; ce sont au contraire de simples variables. Lorsque ces opérateurs sont appliqués à des termes qui ne sont pas des entiers de Church, le résultat est "imprévisible", au sens où l'on ne peut rien dire d'intéressant sur le cas général.
C'est alors une joie de réduire succ 2 en 3 :
( λ n f x . n f ( f x ) )
2 →
λ f x . 2 f ( f x )
→
λ f x .
( λ t . f ( f t ) )
( f x )
→
λ f x . f ( f ( f x ) ) = 3
Commentaires :
Dans la suite de ce chapitre, nous emploierons indistinctement la flèche → pour désigner une β-réduction, ou une suite de β-réductions ; nous écrirons donc : succ 2 → 3. Cette confusion de notations ne devient gênante que pour démontrer le théorème de Church-Rosser (voir section suivante), démonstration qui sort du cadre de ce chapitre d'introduction au λ-calcul.
Enhardis par le succès précédent, additionnons 2 et 3, c'est-à-dire réduisons add 2 3 :
( λ m n f x . m f ( n f x ) )
2 3
→
λ f x . 2 f ( 3 f x )
→
λ f x .
2 f (
f ( f ( f x ) ) )
→
λ f x . f ( f (
f
( f ( f x ) ) ) ) = 5
Remarque : pour passer de la première ligne à la seconde, nous avons effectué deux substitutions en parallèle, une pour chacun des arguments (nous avons substitué 2 à m et 3 à n).
Toujours plus fort, multiplions 2 et 3, c'est-à-dire réduisons mul 2 3 :
( λ m n f . n ( m f ) )
2 3
→
λ f . 3 ( 2 f )
→
λ f . 3
( λ t . f ( f t ) )
Posons M = λ t . f ( f t ), alors 3 M se réduit en : λ x . M ( M ( M x ) ). On a trois réductions possibles, correspondant aux 3 occurrences de M ; choisissons une réduction interne, c'est-à-dire réduisons le terme le plus intérieur (idem pour la réduction suivante) :
λ f x . M ( M ( M x ) )
→
λ f x . M ( M
( f ( f x ) ) )
=
λ f x . M ( M
( f 2 x ) )
→
λ f x . M ( f ( f
( f 2 x ) ) )
=
λ f x . M (
f 4 x )
→
λ f x . f ( f (
f 4 x ) ) = 6
On a choisi une stratégie interne de réduction, y compris lorsqu'on a réduit 3 ( 2 f ) ; on pourra vérifier que le résultat ne dépend pas de la stratégie choisie, c'est le théorème de Church-Rosser — voir section suivante.
Enfin réduisons exp 2 3 :
( λ m n . n m ) 2 3 → 3 2 → λ x . 2 ( 2 ( 2 x ) )
On peut se croire égaré, car on sait réduire 2 f, mais apparemment pas 2 x. Mais les noms de variables sont sans importance ; on a utilisé jusqu'à maintenant f et x pour nous guider, mais le λ-calcul n'est pas typé, aucune variable ne désigne plutôt une fonction ou plutôt un argument ; c'est d'ailleurs cette absence de typage qui nous permet d'appliquer un entier à un autre. Bref, changeons x en f (c'est une α-conversion) pour retrouver nos habitudes :
3 2 → λ f . 2 ( 2 ( 2 f ) ) → λ f . 2 ( 2 ( λ t . f ( f t ) ) )
Posons M = λ t . f ( f t ), et poursuivons la réduction :
λ f . 2 ( 2 M ) ) → λ f . 2 ( λ u . M ( M u ) ) )
Posons N = λ u . M ( M u ), et on obtient :
λ f . 2 N
→
λ f x . N ( N x )
→
λ f x . N (
M ( M x ) )
→
λ f x . M ( M
( M ( M x ) ) )
d'après la définition de N ; reste à utiliser quatre fois la définition de M pour obtenir 8 !
Nous laissons le lecteur méditer sur la puissance du λ-calcul, qui permet de définir aussi simplement l'opérateur d'exponentiation : appliquer un entier à un entier est possible, puisqu'un entier a été défini comme un opérateur !
Le λ-calcul permet de définir très simplement les booléens false et true, ainsi que le test if. Le test if est une fonction de trois variables telle que :
if true M N → M
if false M N → N
Comme pour les entiers, l'idée essentielle est de définir les booléens comme des opérateurs à deux arguments : true sélectionne son premier argument, sans même regarder le second, et false fait l'inverse. Si bien que if devient inutile, mais on le conserve pour la lisibilité des expressions :
true = λ x y . x , false = λ x y . y , if = λ f x y . f x y .
On remarque que le terme false est aussi le codage de 0 en λ-calcul ; par contre les termes qui représentent true et 1 sont distincts.
Le λ-calcul permet aussi de définir raisonnablement les structures de couples et de listes : voir la feuille d'exercices et les références en fin de chapitre (cours de Paulson et de Goubault-Larrecq). Reste essentiellement, pour retrouver la puissance de calcul d'un langage classique, à savoir coder les définitions récursives.
Nous choisirons, sans originalité, l'exemple de la factorielle, et sa définition récursive en C :
int fact (int n) {
if (n == 0) return 1;
else return n * fact (n - 1);
}
Traduit avec les conventions du λ-calcul, cette définition devient :
fact = λ n . if ( iszero n ) 1 ( mul n ( fact ( pred n ) ) )
où l'on suppose déjà définis les termes if, iszero (test de nullité d'un entier) et pred (prédécesseur) — voir la feuille d'exercices pour les détails. L'égalité ci-dessus ne définit pas le terme fact, elle dénote une équation que doit satisfaire ce terme. Par contre on peut définir le terme F suivant :
F = λ f n . if ( iszero n ) 1 ( mul n ( f ( pred n ) ) )
et l'équation qui définit fact devient simplement : fact = F fact , autrement dit fact doit être un point fixe de F. Ici intervient un nouveau miracle du λ-calcul : il existe un terme Y tel que, pour tout terme M, on ait :
Y M → M ( Y M )
Y est appelé opérateur de point fixe, puisqu'il possède la faculté miraculeuse de fabriquer un point fixe pour n'importe quel terme M ! Notons cependant que dans le modèle de calcul utilisé dans les premiers chapitres (programmation impérative en pseudo-C), on sait aussi fabriquer de tels points fixes, voir la feuille d'exercices du chapitre 3.
Il existe d'ailleurs plusieurs termes qui possèdent cette vertu ; le plus simple est le combinateur paradoxal de Curry :
Y = λ f . (λx . f (x x)) (λx . f (x x))
Vérifions :
Y M → (λx . M (x x)) (λx . M (x x)) = N N
en posant N = λx . M (x x) ; et cette définition de N implique : N N → M ( N N ). Nous obtenons donc à la fois :
Y M → N N , d'où : M ( Y M ) → M ( N N )
et, par réduction de N N :
Y M → M ( N N )
ce qu'on peut résumer par :
Y M → M ( N N ) ← M ( Y M )
Le passage du terme du milieu au terme de droite peut être appelé β-expansion : c'est l'inverse d'une β-réduction. Deux termes sont dits β-équivalents si l'on passe de l'un à l'autre par une suite de β-réductions et/ou β-expansions. La β-équivalence est souvent dénotée simplement par le signe d'égalité, mais alors il faut un autre signe, par exemple ≡ , pour exprimer que deux termes sont identiques. Nous ne le ferons pas ici, car nous n'emploierons pas, en dehors de cette section, la β-équivalence.
Un exercice indique une autre définition possible pour Y, un peu plus compliquée, mais telle qu'on ait bien cette fois Y M → M ( Y M ). La définition exacte de Y est d'ailleurs peu importante en pratique, l'essentiel est de savoir qu'un tel opérateur de point fixe existe. On peut maintenant définir :
fact = Y F
d'où la réduction :
fact = Y F → F ( Y F ) = F fact
et on peut calculer par exemple :
fact 3
→
F fact 3
→
→
if ( iszero 3 ) 1
( mul 3 ( fact ( pred 3 ) ) )
→
→
mul 3 ( fact ( pred 3 ) )
La dernière réduction combine la réduction iszero 3 → false, avec la réduction if false M N → N. Poursuivons :
mul 3 ( fact ( pred 3 ) ) → mul 3 ( fact 2 )
et de même :
fact 2 → mul 2 ( fact 1 ) , fact 1 → mul 1 ( fact 0 )
puis :
fact 0 → F fact 0 → if ( iszero 0 ) 1 ( mul 0 ( fact ( pred 0 ) ) ) → 1 .
La dernière réduction combine la réduction iszero 0 → true, avec la réduction if true M N → M. En reportant, on obtient :
fact 3 → mul 3 ( mul 2 ( mul 1 1 ) ) ,
terme qu'on doit pouvoir réduire en 6…
La syntaxe du λ-calcul est extraordinairement simple, et pour l'essentiel il y a une seule règle (la β-réduction) pour "exécuter" un programme. Un calcul termine lorsqu'on obtient un terme irréductible : aucune β-réduction n'est plus possible, par absence de redex, c'est-à-dire de sous-terme de la forme ( λx . M ) N. Chacun des objets de base que nous avons définis précédemment — entiers et opérateurs sur les entiers (addition, produit, etc.), booléens et opérateurs logiques — sont des termes irréductibles, à l'exception notable du terme fact qui définit la factorielle (nous y reviendrons).
Un calcul est essentiellement non déterministe (un terme possède en général plusieurs redex), et il faut donc examiner si différentes stratégies de réduction d'un terme (c'est-à-dire différents choix du prochain redex à réduire) influent sur le résultat final obtenu. Le théorème fondamental est le suivant :
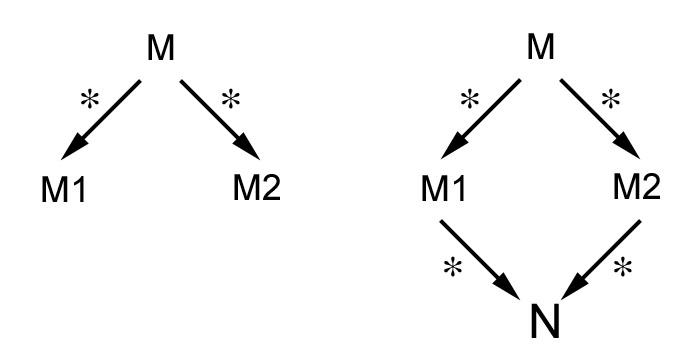
Théorème de Church-Rosser. Si le terme M peut être réduit en M1 d'une part, et en M2 d'autre part, alors il existe un terme N tel qu'on puisse réduire à la fois M1 et M2 en N. |
 |
Ce théorème exprime que le diagramme de gauche peut toujours être complété en celui de droite (attention : les étoiles indiquent que chaque flèche désigne une suite de réductions). Autrement dit, les réductions qui ont transformé M en M1 peuvent être "dupliquées" pour transformer M2 en N, et vice-versa, en échangeant les rôles de M1 et M2 . Obtenir une démonstration élégante de ce théorème est assez long et délicat, nous ne le ferons pas ; voir les deux premières références en fin de chapitre.
Supposons maintenant que M puisse être réduit en M1 et M2 irréductibles ; d'après le théorème de Church-Rosser, les termes M1 et M2 peuvent être réduits en un même terme N ; comme par ailleurs M1 et M2 sont irréductibles, on en déduit que M1 = M2 = N. Autrement dit :
Si le calcul de M termine, le terme final N (irréductible par définition) ne dépend pas de la stratégie choisie ; on dit que N est la forme normale de M.
Examinons maintenant les calculs qui ne terminent pas, puisqu'on sait depuis le chapitre 2 que de tels calculs sont inévitables dans tout modèle de calcul universel. La situation est plus complexe qu'on ne le souhaiterait, car il existe des termes (et donc des calculs) dont la terminaison dépend de la stratégie choisie !
L'exemple classique de terme qui ne possède pas de forme normale est le suivant :
Ω = ( λ x . x x ) ( λ x . x x )
En effet, on vérifie facilement qu'en appliquant à Ω la seule β-réduction possible, on obtient … Ω ; et ainsi de suite indéfiniment. Ce n'est pas étonnant, car D = λ x . x x est la traduction en λ-calcul de l'opérateur diagonal du chapitre 2 ; et comme au chapitre 2, l'application de D à lui-même ne peut que "boucler".
L'exemple du terme fact (factorielle), défini section 3, est plus troublant, car on a une suite infinie de réductions :
fact → F fact → F ( F fact ) → …
Bien sûr on peut choisir de réduire le redex F fact, mais les termes obtenus contiennent toujours une occurrence de fact, et ne sont donc jamais irréductibles : fact n'a pas de forme normale. Par contre, on l'a vu, fact 3 peut être réduit en 6, qui est un terme irréductible. Il existe donc des expressions qui possèdent des formes normales, bien que des termes qui la composent n'en possèdent pas ! Et une stratégie consistant à traiter fact 3 par réduction indéfinie de fact en F fact (sans jamais se préoccuper de l'argument) ne termine pas.
On peut évidemment chercher à réduire n'importe quel λ-terme, mais en pratique le cas intéressant est celui où l'on applique un terme A, censé représenter une fonction, à un argument U. Si A est de la forme λx . B (c'est le cas des opérateurs add, mul, etc.), une stratégie externe consiste à réduire immédiatement le redex :
A U = ( λx . B ) U → B [ U / x ]
c'est à dire à remplacer toute occurrence libre de x dans B par U. L'argument U peut être un terme complexe, qu'on se contente de dupliquer autant de fois que x apparaît dans B ; une telle stratégie est aussi appelée, en informatique, appel par nom.
Il se peut que A ne soit pas de la forme λx . B : c'est le cas de fact ; dans cette situation, une stratégie externe gauche réduit récursivement A jusqu'à se ramener au cas précédent. Par exemple, pour réduire fact U, il faut commencer par réduire fact en F fact :
fact U → F fact U → if ( iszero U ) 1 ( mul U ( fact ( pred U ) ) )
car F = λ f n . if ( iszero n ) 1 ( mul n ( f ( pred n ) ) ), et l'on vérifie facilement que les conventions sur les fonctions à plusieurs variables entraînent que la stratégie externe revient à substituer simultanément les arguments (ici fact et U) aux variables (ici f et n). On voit sur cet exemple que l'argument U a été dupliqué trois fois, ce qui n'est certainement pas une stratégie efficace si U est un terme complexe, qui après de longs calculs, se réduit par exemple à 4 : il faudra maintenant répéter peut-être trois fois ces longs calculs.
Une stratégie externe gauche est sûre : si on l'applique à un terme M qui possède une forme normale N, le calcul termine.
La démonstration est à nouveau assez délicate, et nous ne la donnerons pas ; par contre il est vivement conseillé, pour bien comprendre le fonctionnement d'une stratégie externe, de poursuivre la réduction de fact U, en appliquant rigoureusement une stratégie externe gauche, et en supposant que la forme normale de U est 4 (voir corrigé sur la feuille d'exercices).
Revenons à la réduction de A U, où A est un terme censé représenter une fonction, et U un argument. Une stratégie interne consiste à commencer par réduire autant que possible A et U ; on mène les calculs en choisissant toujours un redex interne (c'est-à-dire qui ne contient aucun autre redex).
Une stratégie interne gauche réduit A avant de réduire l'argument U, et c'est évidemment l'inverse pour une stratégie droite. Evaluer l'argument avant d'exécuter un appel de fonction est la stratégie adoptée lorsqu'on programme en langage C, car c'est usuellement la plus efficace : on évite des évaluations répétées du même argument ; cette stratégie est appelée appel par valeur. En programmation impérative, évaluer A est immédiat, puisqu'il s'agit de l'adresse de la procédure à exécuter ; en λ-calcul, l'évaluation de A est souvent nécessaire et aussi longue que l'évaluation de l'argument U : c'est le cas de fact, mais aussi des booléens, puisque ce sont des opérateurs qu'on doit réduire à true ou false avant de les appliquer à leurs arguments ; idem pour les entiers, qui ne sont pas des arguments inertes, mais des opérateurs qu'il faut évaluer avant de les faire agir.
L'appel par valeur ne fonctionne qu'avec une convention restrictive, qui "va de soi" en programmation impérative ; pour exécuter une instruction :
if ( P ) U else V
on commence par évaluer le prédicat P, puis on exécute soit U soit V (mais pas les deux !) selon le résultat du test. En λ-calcul, une stratégie interne stricte consiste à évaluer à la fois P, U et V avant d'évaluer l'expression conditionnelle, ce qui n'est pas très malin. En particulier, dans le cas de la factorielle, cette stratégie conduit à une suite infinie de réductions de fact, car :
fact 0
→
if ( iszero 0 ) 1
( mul 0
( fact ( pred 0 ) ) )
→
→
if true 1
( mul 0
( fact ( pred 0 ) ) )
et une stratégie interne se poursuit (stupidement) par :
pred 0 → 0 , d'où
fact 0
→ … →
if true 1
( mul 0
( fact 0 ) )
et la suite de réductions internes boucle.
Le λ-calcul se trouve donc dans une situation embarrassante : une stratégie externe est sûre, mais inefficace, tandis qu'une stratégie interne stricte conduit fréquemment à des calculs sans fin, alors que le terme à réduire possède une forme normale. Bien entendu, on a cherché des compromis, en particulier l'appel par nécessité, ou évaluation paresseuse (lazy evaluation) ; ces travaux sont intéressants (voir les références en fin de chapitre), mais aucune des stratégies proposées ne s'est révélée être une panacée.
D'autre part les entiers de Church n'ont qu'un intérêt théorique, en pratique un langage fonctionnel utilise la représentation binaire des entiers, et les opérations du processeur sur ces entiers ; ce qui implique, d'une façon ou d'une autre, l'apparition de types, et de règles spéciales d'évaluation selon ces types.
Notons pour terminer que certaines des difficultés présentées dans cette section apparaissent aussi en programmation impérative ; une instruction comme :
while ( i >= 0 && x != t [i] ) …
ne doit surtout pas provoquer une tentative d'évaluation de t[i] lorsque l'indice i est négatif. Cela semble aller de soi, mais un compilateur inclut un optimiseur, pour la phase de production de code, et ce n'est pas si facile d'éviter que la réorganisation du code n'entraîne des bugs du type ci-dessus ! De même, la structure en pipe-line de tous les processeurs modernes demande, pour être aussi efficace que possible, qu'un début d'évaluation des deux branches d'une alternative ait lieu en même temps que le calcul du prédicat qui décide de la branche à suivre.
Le λ-calcul constitue un modèle d'une puissance équivalente à celui de Von Neumann, qui décrit l'architecture des processeurs usuels, ou à celui des machines de Turing. Une fonction f : N → N est dite λ-définissable s'il existe un λ-terme F tel que, pour tout entier x :
où x (resp. y) désigne, comme d'habitude, l'entier de Church associé à l'entier x (resp. y). Notons que y est irréductible, c'est donc la forme normale de F x dans le premier cas ci-dessus. On peut alors montrer qu'une fonction est λ-définissable si et seulement si elle est calculable, au sens des premiers chapitres de ce cours, ou au sens des machines de Turing.
Nous ne donnerons pas de démonstration ; on passe usuellement par le modèle intermédiaire des fonctions récursives, et on prouve qu'une fonction est λ-définissable si et seulement si elle peut être construite à partir de fonctions arithmétiques de base (comme la fonction successeur) et de trois opérateurs (composition, récursion primitive, et minimisation), qui permettent de fabriquer récursivement toutes les fonctions calculables.
En fait considérer, comme ci-dessus, qu'un terme sans forme normale est indéfini, n'est pas satisfaisant, pour différentes raisons théoriques, qui sortent du cadre de ce cours. Constatons simplement que fact n'a pas de forme normale, mais qu'on peut difficilement soutenir que ce terme est simplement indéfini, puisque le calcul de fact 3 termine.
Le remède est de renforcer la contrainte sur un terme pour qu'il soit déclaré indéfini : un tel terme ne doit pas posséder de forme normale de tête (head normal form, en abrégé hnf) ; voir Paulson, section 4.5, ou le cours de Goubault-Larrecq, section 3.4 (Standardisation et appel par nom) pour la définition et quelques développements. Un terme sans hnf est dit aussi irrésoluble (unsolvable) ; une forme normale est un cas particulier de hnf, et donc un terme irrésoluble ne possède pas de forme normale ; mais la première condition (à savoir : irrésoluble) est plus forte que la seconde (à savoir : pas de forme normale), car si A est irrésoluble, il en est de même du terme A U, quel que soit U ; en particulier fact n'est pas irrésoluble. On a vu ci-dessus qu'une stratégie externe gauche fournit la forme normale d'un terme qui en possède une ; ce résultat s'étend aux hnf. Enfin on peut améliorer le résultat donné en début de section ; si f est une fonction calculable partielle, on peut lui associer un λ-terme F tel que, pour tout entier x :