Arbres avec au plus 5 arêtes
Tous ces arbres sont rationnels,
au sens où les coefficients de leurs polynômes de Shabat
sont rationnels.
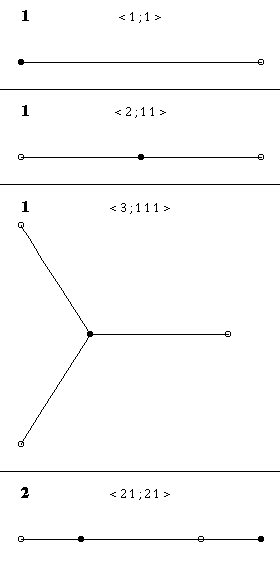
Arbres avec au plus 3 arêtes
Les polynômes de Shabat sont affichés à gauche des arbres ;
tous sont triviaux sauf le dernier, qui est un
polynôme de Tchebycheff.
Arbres avec 4 arêtes
Il y a trois passeports, c'est-à-dire trois
assortiments de degrés.
| z4
| 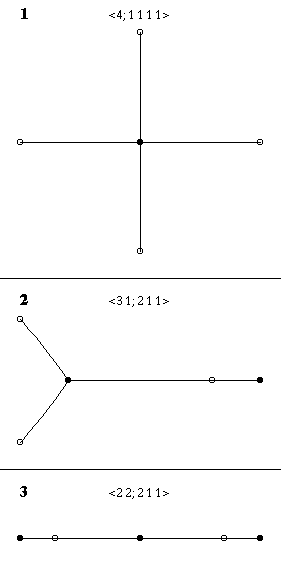
|
| z3 (1 - z)
|
| 8z4 - 8z2 + 1
|
Le dernier polynôme (arbre 3 en forme de chaîne)
est un polynôme de Tchebycheff.
Détails de l'arbre 2 (passeport <3 1; 2 1 1>) :
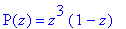
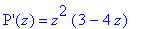
-
les points critiques sont 0 et 3/4
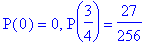
- les valeurs critiques sont 0 et 27/256
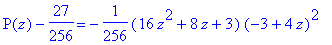
-
l'arbre dessiné est l'image réciproque du segment
[0 27/256]
-
les sommets noirs sont les images réciproques de 0
-
les sommets blancs sont les images réciproques de 27/256
-
le sommet noir d'affixe 0 est de degré 3
et celui d'affixe 1 de degré 1
-
le sommet blanc d'affixe 3/4 est de degré 2
et les deux autres sont de degré 1.
Arbres avec 5 arêtes
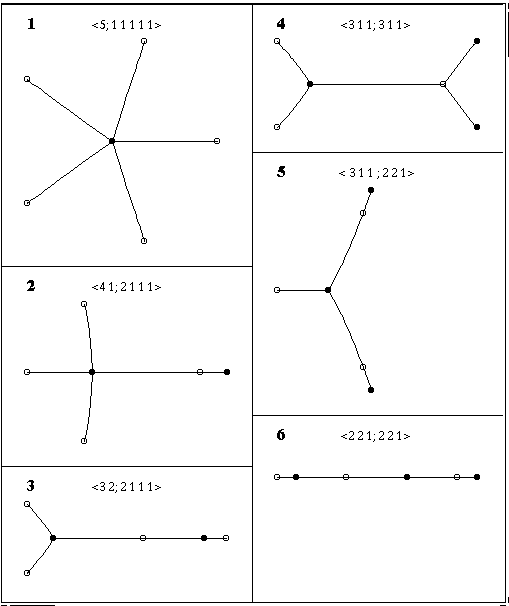
Polynômes de Shabat :
Note : exceptionnellement p4 ne s'annule pas en 0,
les points critiques triples sont -1 et 1,
on les a choisis ainsi (au lieu du choix habituel 0 et 1) pour respecter
la symétrie du passeport.


![]()
![]()
![]()
![]()
