Fn = Fn-1 + Fn-2 , pour n > 1.
D'où une fonction C qui calcule le nème terme de la suite :
long fibonacci (int n) {
int i;
long a = 0, b = 1, c;
for (i = 2 ; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
|
|
|
|
|
|
La théorie classique des récurrences linéaires montre qu'on a :
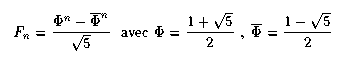
Phi est le nombre d'or, qui vaut approximativement 1.618 ; le module de son conjugué vaut approximativement 0.618, et donc son influence dans la formule ci-dessus est rapidement négligeable. En particulier le rapport entre deux termes consécutifs de la suite de Fibonacci tend vers le nombre d'or.