
et après l'avoir déterminisé et renommé les états on obtient:
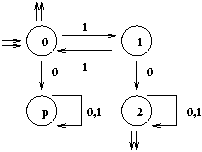
où p désigne l'état ``puits''.
Pour n quelconque l'automate non déterministe a la structure suivante:
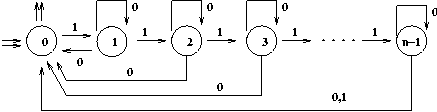
``Tous les états de l'automate obtenu en déterminisant sont accessibles''.
Pour cela on définit l'ordre suivant dans P(Q) (les états obtenus en déterminisant sont des ensembles, parties de P(Q)):
- on réprésente une partie A de P(Q) par un mot i1i2 ... ik avec i1 < i2 < ... < ik avec ij compris entre 0 et n-1.
- on ordonne les parties de la façon suivante:
A < B si et seulement si:
soit |A|<|B|
soit |A|=|B| et A <=lex B
(c.a.d. que soit A est plus courte que B, soit A précède B dans l'ordre lexicographique)
C'est clairement un ordre total sur P(Q):
(0),(1),(2), ... (n-1),(0,1),(0,2), ... (0,n-1),(1,2),
... (0,1,2), ... (0,1,2, ...,n-1)
et on peut donc parler de rang r d'une partie.On prouve maintenant la propriété:
- Elle est vraie pour le rang 1 (l'état initial est accessible).
- On la prouve pour le rang p:
supposons que tout état de rang inférieur à p soit accessible, soit A un état de rang p, A= (i1,i2, ... ik).
Deux cas se présentent:
1. i1 différent de 0, mais alors
delta((i1-1,i2-1,... ik-1),1)= (i1,i2, ... ik)
avec l'état (i1-1,i2-1,... ik-1) de rang
inférieur à p et donc accessible par hypothèse.2. i1 égal à 0, mais alors
delta((i2, ... ik),0)= (0,i2, ... ik)
avec l'état (i2, ... ik) de rang
inférieur à p et donc accessible par hypothèse.