B*L = BB*L + L = (BB* + epsilon)L = B*L
C'est la plus petite solution: soit Y une autre solution, plus petite de X0, alors Y est un sous-ensemble de B*L et Y = BY + L et donc (en substituant BY + L à Y):
Y = B2Y + BL + L = B3Y + B2L + BL + L = ... = BnY + Bn-1L + ... + L.
On a BnL sous-ensemble de Y, pour tout n dans IN et donc B*L est sous-ensemble de Y. Mais on a aussi supposé Y sous-ensemble de B*L et donc Y = B*L.
Y = Bn+1Y + BnL + Bn-1L + ... + BL + L. Soit w un mot de Y avec |w| = n, alors compte tenu que B ne contient pas epsilon, w est dans BnL + Bn-1L + ... + BL + L et donc w appartient à B*L.
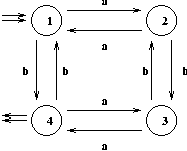
Si l'on pose Li = {u dans {a,b}*tels que delta*(i,u)= 4 }, on a L = L1.
On a donc le système:
| L1 | = | aL2 + bL4 |
| L2 | = | aL1 + bL3 |
| L3 | = | aL4 + bL2 |
| L4 | = | aL3 + bL1 + epsilon |
Qu'on résoud par rapport à L1:
| L1 | = | a2L1 + abL3 + baL3 + b2L1 + b |
| = | (a2 + b2)L1 + (ab + ba)L3 + b | |
| L3 | = | a2L3 + abL1 + a + baL1 + b2L3 |
| = | (a2 + b2)L3 + (ab + ba)L1 + a | |
| = | (a2 + b2)*((ab + ba)L1 + a) | |
| = | (a2 + b2)*(ab + ba)L1 + (a2 + b2)*a | |
| L1 | = | (a2 + b2)L1 + (ab + ba)(a2 + b2)*(ab + ba)L1 + (ab + ba)(a2 + b2)a + b |
| = | ((a2 + b2) + (ab + ba)(a2 + b2)*(ab + ba))L1 + (ab + ba)(a2 + b2)a) + b | |
| = | ((a2 + b2) + (ab + ba)(a2 + b2)*(ab + ba))* ((ab + ba)(a2 + b2)a + b) |