Back to Tutte's original equation (Section 14.2)
We start from the equation for Q that involves t, z and w (the first equation of the session)
| > | eqQ; |
![]()
![]()
The equation of Lemma 31
| > | unassign('R'):eqQR:=1+Q(x,y)/Q(0,y)*R(x,Y)-Q(x,y); |
![]()
| > | Ydef:=y*Q(0,y); |
![]()
We now constrcut an equation for R
| > | subs(x=0,eqQR); |
![]()
| > | Q0ysol:=solve(%,Q(0,y)); |
![]()
| > | Qxysol:=solve(subs(Q(0,y)=Q0ysol,eqQR),Q(x,y)); |
![]()
| > | subs(Q(0,0)=1, Q(x,0)=1,R(x,0)=0,series(subs(Y=Ydef,eqQR),y,1)); |
![]()
| > | subs(Q(0,0)=1, Q(x,0)=1,R(x,0)=0,series(subs(Y=Ydef,eqQR),y,2)); |
![]()
| > | normal(subs(Q(0,0)=1, Q(x,0)=1,R(x,0)=0,D[2](R)(x,0)=D[2](Q)(x,0),series(subs(Y=Ydef,eqQR),y,3))); |
![]()
| > | eqR0:=subs(Q(x,y)=Qxysol, Q(0,y)=Q0ysol, y=Y/Q0ysol, Q1(x)=R1(x), Q2(x)=R2(x)+R1(x)^2,eqQ); |
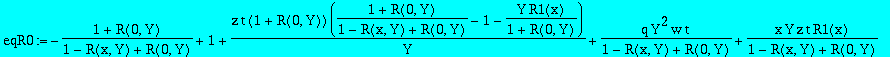
![]()
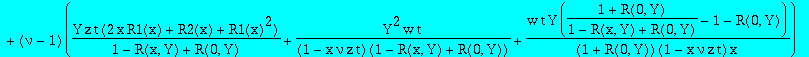
| > | indets(%); |
![]()
| > | eqR1:=-op(2,factor(numer(subs(Y=y,eqR0)))); |
![]()
![]()
![]()
![]()
![]()
| > | subs(t=0,eqR1); |
![]()
| > | eqR2:=eqR1/x/y; |
![]()
![]()
![]()
![]()
![]()
Version of the paper
| > | papier:=-R(x,Y)+ y^2*w*t*(1-x*nu*z*t)*q+(nu-1)*w*t*y^2 +x*z*t*(1+nu-x*nu*z*t)*R(x,Y)+x*z*t*Y*(1-x*nu*z*t)*R1(x)+ z*t*(1-x*nu*z*t)*R1(x)*R(x,Y) +z*t*(1-x*nu*z*t)*(1+R(0,Y))* (R(x,Y)-Y*R1(x))/Y +(nu-1)* Y*z*t*(1-x*nu*t*z)*(R2(x)+R1(x)^2+2*x*R1(x)) +(nu-1)*w*t*Y*(R(x,Y)-R(0,Y)) /x; |
![]()
![]()
| > | collect(factor(eqR2/subs(Y=y,papier)),R1(x),factor); |
![]()
Non-separable maps of Q: set nu=0 in the previous equation. Then R1=0=S1
| > | eqS:=factor(numer(subs(R=S,R1(x)=0,R2=S2,nu=0,eqR2))); |
![]()
We finally reach Tutte's series T. Denote X=1/(1-xz) (see lemma 33)
| > | eqT:=numer(factor(subs(w=1,t=1, S(x,y)=T(X,y)/q, S2(x)=T2(X)/q, S(0,y)=T(1,y)/q,x=(1-1/X)/z,X=x,eqS))); |
![]()
![]()
Version de Tutte
| > | eqTutte:=x*y^2*q*(q-1)+x*z/y/q*T(1,y)*T(x,y)+x*z*(T(x,y)-y^2*T2(x))/y-x^2*y*z*(T(x,y)-T(1,y))/(x-1)-T(x,y); |
![]()
| > | factor(eqT/eqTutte); |
![]()
| > |