The case q=1 (m=3,k=1) (Section 11.1)
Chebyshev polynomials
| > | T:=proc(m) subs(cos(x)=x,expand(cos(m*x))): end: |
| > | T(3); |
![]()
| > | m:=3: k:=1: 2+2*cos(2*k*Pi/m); |
![]()
Introduce the series K. The second invariant is
| > | I2:=normal(subs(C=CC,II=I1,Q(0,y)=K(y)/t^2/y/q,q=1,sqrt(C)^m*subs(x=xsubs,T(m)))); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | indets(I2); |
![]()
| > | factor(series(normal(I2),y,1)); |
![]()
The invariant equation
| > | eqinv:=subs(q=1,Q(0,y)=K(y)/t^2/y/q,q=1,beta=nu-1,I2-add(c[i]*(t*I1)^i,i=0..3)); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
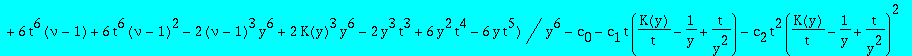
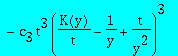
| > |
Determination of the series c_i