Some minor calculations in Section 11 (Lemmas 19 and 20)
End of the proof of Lemma 19
| > | x1:=((nu-1)*(4-q)*z+q*nu*(z^2-z)+(nu-1)*(q-2))/2/sqrt(q*nu^2*(z^2-z)^2+(nu-1)*(4*(nu-1)+q)*(z^2-z)+(nu-1)^2); |
![]()
| > | x2:=subs(z=1-z,x1); |
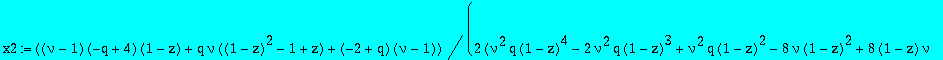
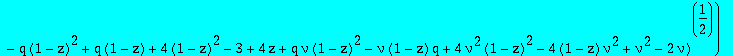
| > | factor(x1^2+x2^2-(q-2)*x1*x2-q*(4-q)/4); |
![]()
| > |
| > |
| > |
| > |
| > |
| > |
End of the proof of Lemma 20
| > | unassign('m'): |
The value of LHS, when t=0 (Eq. 82). We denote z=t/y
| > | Jinv:=subs(y=t/z,C=CC,II=(K-z+z^2)/t,t=0,CC^(m/2)*TT(xsubs)); |
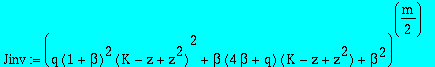
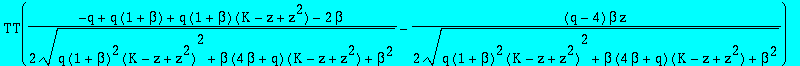
The coefficient of K*z , ie [x ] L_1(x,0)
| > | e1:=collect(simplify(collect(factor(subs(K=0,z=0,diff(diff(Jinv,K),z))),TT,factor),symbolic),TT,factor); |
![]()
![]()
![]()
The first derivative D(TT) is zero
| > | e1:=subs(D(TT)(1/2*q-1)=0,collect(simplify(collect(factor(subs(K=0,z=0,diff(diff(Jinv,K),z))),TT,factor),symbolic),TT,factor)); |
![]()
| > | expand(subs(z=(1-sqrt(1+4*u))/2,z^2-z)); |
![]()
| > | simplify(normal(series(subs(K=0,z=(1-sqrt(1+4*u))/2,Jinv),u,3)),symbolic); |
![]()
![]()
![]()
![]()
![]()
| > | e2:=collect(coeff(%,u,2),TT,factor); |
![]()
![]()
| > | collect(e1+2*e2,TT,factor); |
![]()
| > | res:=subs(D(TT)(1/2*q-1)=0,%); |
![]()
Derivatives of the Chebyshev polynomials
| > | diff(TT(cos(t))-cos(m*t),t); |
![]()
Donc T'(cos(2k pi/m))=0
| > | diff(%,t); |
![]()
| > | subs(D(TT)(cos(t))=0,cos(m*t)=1,%); |
![]()
Second derivative
| > | factor(subs(`@@`(D,2)(TT)(1/2*q-1)=-m^2/(1-((q-2)/2)^2), res)); |
![]()
| > | factor(-m^2/(1-((q-2)/2)^2)); |
![]()
| > |
| > |
| > |