The case q=2 (m=4,k=1) (Section 12.2)
| > |
T:=proc(m) subs(cos(x)=x,expand(cos(m*x))): end:
|

| > |
m:=4: k:=1: 2+2*cos(2*k*Pi/m);
|

The second invariant
| > |
I2:=normal(subs(C=CC,II=I1,q=2,sqrt(C)^m*subs(x=xsubs,T(m)))):
|

| > |
factor(series(normal(I2),y,1));
|

The invariant equation
| > |
eqinv:=subs(q=2,Q(0,y)=Q(y),beta=nu-1,I2-add(c[i]*(t*I1)^i,i=0..4)):
|
Determination of the series c_i. An equation with one catalytic variable and 2 additional unknown series Q'(0) and Q'''(0)
Solution using Tutte's trick
| > |
RHS:=map(factor,collect(subs(c[4]=c4sol,c[3]=c3sol,c[2]=c2sol,c[1]=c1sol,c[0]=c0sol,add(c[i]*(t*X)^i,i=0..4)),Q));
|
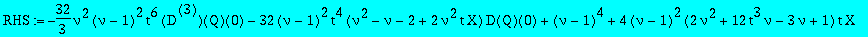
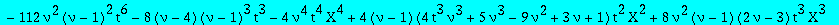

Each of the following polynomials in X has a double root.
We denote by Q_i the series counting quasi-triangulations with outer degree i.
| > |
pol1:=collect(op(3,factor(subs(`@@`(D,3)(Q)(0)=6*Q3,D(Q)(0)=Q1,beta=nu-1,factor(subs(q=2,II=X,RHS-CC^2))))),[Q1,Q3,X],factor);
pol2:=collect(op(3,factor(subs(`@@`(D,3)(Q)(0)=6*Q3,D(Q)(0)=Q1,beta=nu-1,factor(subs(q=2,II=X,RHS+CC^2))))),[Q1,Q3,X],factor);
|
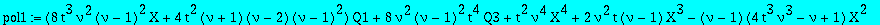
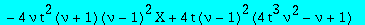
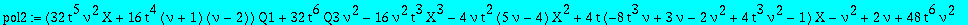
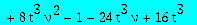
| > |
eq1:=factor(discrim(pol1,X)):
|

| > |
seq(nops(op(i,eq1)),i=1..5);
|

| > |
seq(op(i,eq1),i=1..4);;
|

A first equation between Q1 and Q3
| > |
eq1:=collect(op(5,eq1),[Q1,Q3],factor);
|
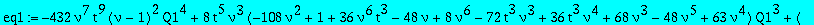
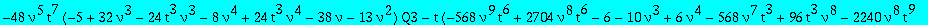
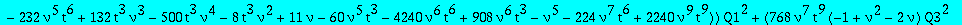
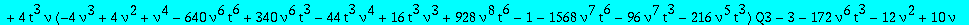
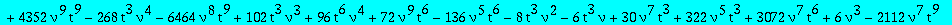
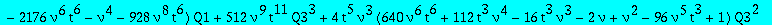
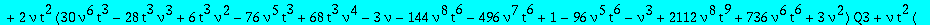
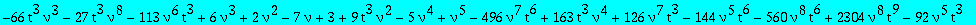
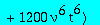
| > |
eq2:=factor(discrim(pol2,X)):
|

| > |
seq(nops(op(i,eq2)),i=1..4);
|

| > |
seq(op(i,eq2),i=1..3);;
|

Second equation between Q1 and Q3
| > |
eq2:=collect(op(4,eq2),[Q1,Q3],factor);
|
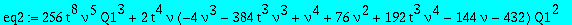
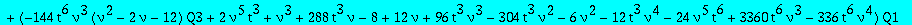
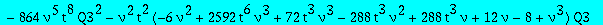
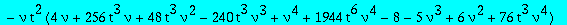
We finally eliminate Q3
| > |
res:=factor(resultant(eq1,eq2,Q3)):
|

| > |
seq(nops(op(i,res)),i=1..5);
|

| > |
op(1,res); op(2,res);op(3,res);
|



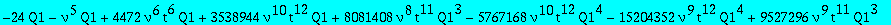
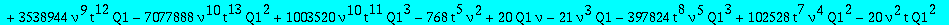
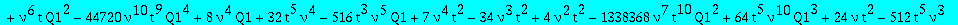
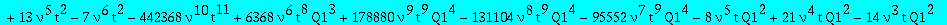
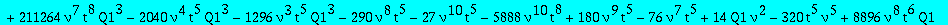
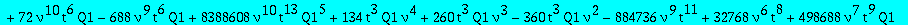
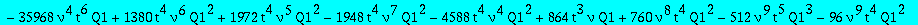
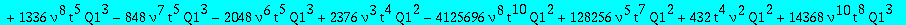
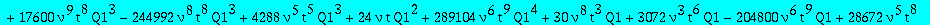
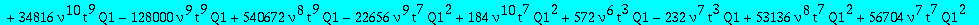
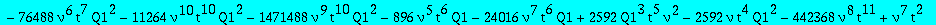
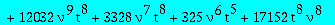
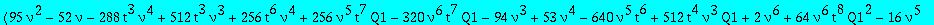
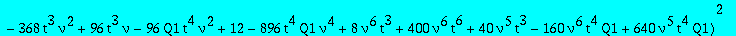
Two candidates for the minimal polynomial of Q1
| > |
alg1:=collect(op(4,res),Q1,factor);
|
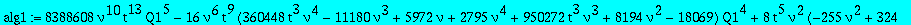
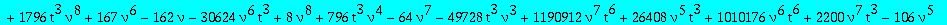
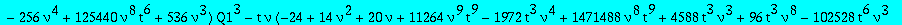
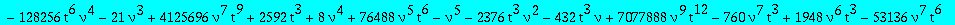
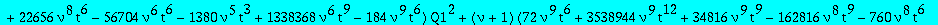
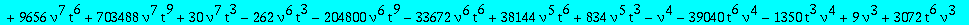
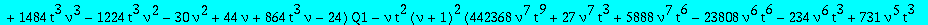
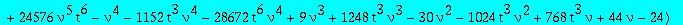

The second candidate
| > |
alg2:=collect(op(1,op(5,res)),Q1,factor);
|
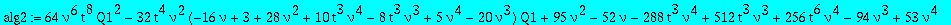
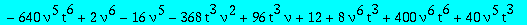

Let us decide
| > |
n:=2:normal(series(subs( Q1=normal(collect(coeff(subs(x=0,w=1,z=1,q=2,Qser(3*n)),y,1),t)),alg2),t,n+1));
|

| > |
n:=4:normal(series(subs( Q1=normal(collect(coeff(subs(x=0,w=1,z=1,q=2,Qser(3*n)),y,1),t)),alg1),t,n+2));
|

Hence the minimal polynomial of Q1 has degree 5. Let us check
| > |
factor(algeqtoseries(alg1,t,Q1,10,true));
|
![[series((nu+1)*nu*t^2+4*nu^2*(nu+1)*(nu^2+1)*t^5+4*nu^3*(nu+1)*(8*nu^4+2*nu^3+9*nu^2+4*nu+9)*t^8+16*nu^4*(nu+1)*(21*nu^6+11*nu^5+28*nu^4+21*nu^3+36*nu^2+24*nu+27)*t^11+O(t^12),t,12)]](images/Potts-triang-paper209.gif)
![[series((nu+1)*nu*t^2+4*nu^2*(nu+1)*(nu^2+1)*t^5+4*nu^3*(nu+1)*(8*nu^4+2*nu^3+9*nu^2+4*nu+9)*t^8+16*nu^4*(nu+1)*(21*nu^6+11*nu^5+28*nu^4+21*nu^3+36*nu^2+24*nu+27)*t^11+O(t^12),t,12)]](images/Potts-triang-paper210.gif)
| > |
n:=4:map(factor,collect(coeff(subs(x=0,q=2,w=1,z=1,Qser(3*n)),y,1),t));
|

In the series t*Q1, denoted Q1t below, all exponents of t are multiples of 3. We denote t^3=w.
| > |
alg1t:=collect(subs(t=w^(1/3),factor(numer(subs(Q1=Q1t/t,alg1)))),Q1t,factor);
|
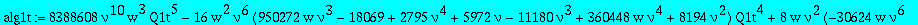
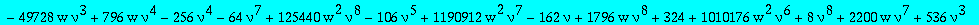
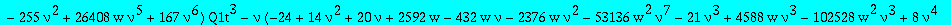
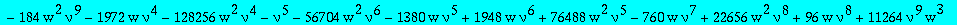
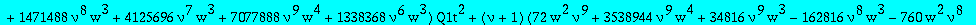
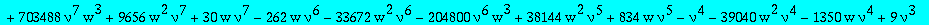
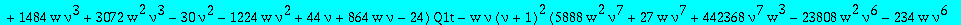
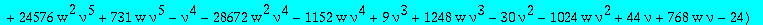


The parametrization of the paper (with v=(nu+1)/(nu-1))
| > |
wS := 1/64*(-2*v-2*S+4*S^3-S^2+v^2)*(-S+v)*(S-2+v)/S^2/(1+v)^3;
|

let us check that it indeed factors the minimal polynomial of Q1
| > |
res:=numer(factor(subs(w=wS,nuv,alg1t))):
|




The right factor is not op(3,res), but the linear one
| > |
factor(subs(S=v,Q1t=0,op(3,res)));
|

| > |
Q1tsol:=factor(solve(op(2,res),Q1t));
|

Expression of Q3? We get back to one of the equation we had between Q1 and Q3, and introduce Q3t:= t^3 Q3
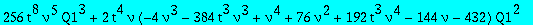
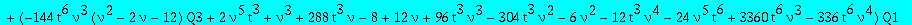
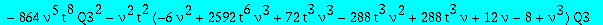
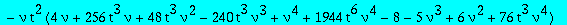
| > |
subs(t=w^(1/3),numer(factor(subs(Q1=Q1t/t,Q3=Q3t/t^3,eq2))));
|
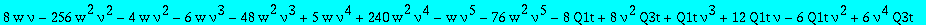
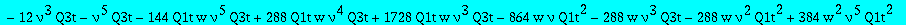
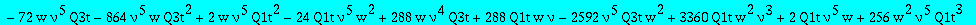
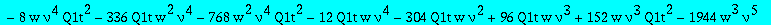
| > |
res:=numer(factor(subs(nuv,Q1t=Q1tsol,w=wS,%)));
|
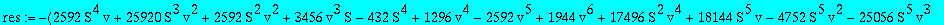
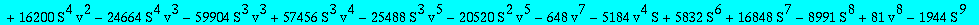
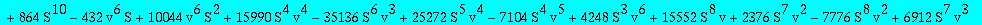
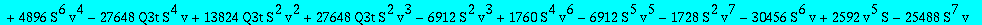
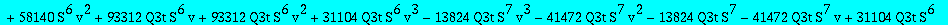
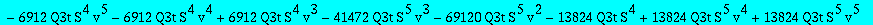
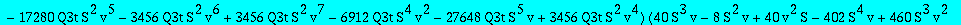
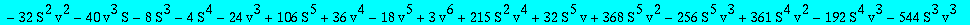
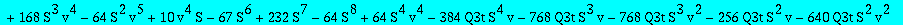
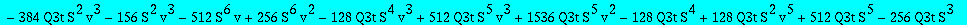
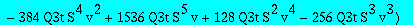

| > |
degree(op(3,res),Q3t);degree(op(2,res),Q3t);
|


The right factor is op(3,res):
| > |
factor(subs(S=v,Q3t=0, op(3,res)));factor(subs(S=v,Q3t=0, op(2,res)));
|


| > |
Q3tsol:=factor(solve(op(3,res),Q3t));
|
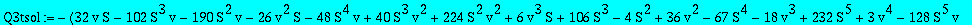
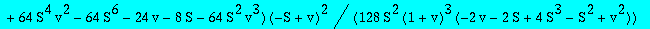
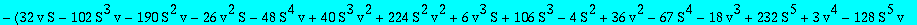
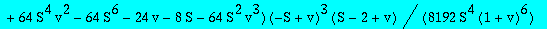
Asymptotics
![]()
![]()
![]()
![]()