TD 2
Exercice 1
Expliquer ce que fait chacun des programmes suivants. Pour chaque exemple, vous préciserez le contenu de la mémoire et l'affichage à chaque étape de l'exécution du programme.
-
def fct(u) : u=6 u=3 fct(u) print(u) -
def fct(u) : return 6 u=3 fct(u) print(u) -
def fct(u) : return 6 u=3 u=fct(u) print(u) -
def fct(u) : print(u) u=3 fct(u) print(u)
-
def fct(u) : print(u) u=3 u=fct(u) print(u)
-
def fct(u) : print(6) return 6 u=3 fct(u) print(u) -
def fct(u) : return 6 print (6) u=3 fct(u) print(u)
Exercice 2: Intersection de droites
-
Soient deux points du plan
M=(xm,ym)etN=(xn,yn).Écrire un programme
equation_de_droite(xm,ym,xn,yn)qui renvoie un triplet(a,b,c)qui code l'équation cartésiennea.x+b.y+c=0de la droite qui passe par les deux pointsMetN. -
Soient deux équations du premier degré
a.x+b.y+c=0etd.x+e.y+f=0.Écrire un programme
solution_equations_de_droite(a,b,c,d,e,f)qui prend en paramètres les réelsa,b,cetd,e,fet qui renvoie :-
Nonesi la solution n'existe pas ou n'est pas unique; -
Le couple
(xs,ys)qui est l'unique solution aux équations précédentes.
-
-
Soient quatre points du plan
A=(xa,ya),B=(xb,yb),C=(xc,xd)etD=(xd,yd).Écrire un programme
intersection_de_droite(xa,ya,xb,yb,xc,yc,xd,yd)qui renvoie:-
Nonesi la droite (A,B) et la droite (C,D) ne se coupent pas en un point; -
Le couple
(x,y)qui représente les coordonnées en x et y de l'intersection de la droite (A,B) avec la droite (C,D).
-
Exercice 3: Exécution d'un programme
Voici quelques programmes:
def mystere1(a):
if 0>a:
x = -a
return x
def mystere2(a,b):
if a>b:
return a
else:
return b
def mystere3(t):
if 0>t:
return 0
def mystere4(x,m):
res = 1
for i in range(m):
res = res*x
return res
def mystere5(n):
r = n
while r>=10:
r = r/10
return r
def mystere6(n,b):
r = n
while r>=b:
r = r/b
return r
Prévoir le résultat des fonctions mystere pour différents paramètres.
Proposer une description de ce qu'elles sont censées calculer.
Si une des fonctions ne vous paraît pas fonctionner correctement, proposez une correction.
Exercice 4: Conjecture de Syracuse
On définit la suite de Syracuse d'un entier N donné, comme étant la suite 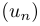 définie par récurrence par :
définie par récurrence par :
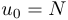 et pour tout entier
et pour tout entier 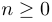 ,
,
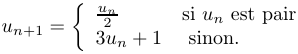
Une célèbre conjecture, appelée conjecture de Syracuse, affirme que quelque soit le terme de départ 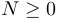 , la suite de Syracuse de N finit toujours par atteindre 1 (autrement dit, il existe toujours un entier n tel que
, la suite de Syracuse de N finit toujours par atteindre 1 (autrement dit, il existe toujours un entier n tel que 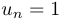 ).
Cette conjecture a été vérifiée à l'aide d'ordinateurs pour toutes les valeurs possibles de N comprises entre 1 et
).
Cette conjecture a été vérifiée à l'aide d'ordinateurs pour toutes les valeurs possibles de N comprises entre 1 et 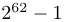 .
Cependant, aucune démonstration mathématique n'existe encore à l'heure actuelle.
.
Cependant, aucune démonstration mathématique n'existe encore à l'heure actuelle.
-
Écrire une fonction
Syracuse(N,n)qui retourne le terme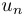 de la suite de Syracuse de N.
de la suite de Syracuse de N.
-
Écrire une procédure
premiers_Syracuse(N,k)qui affiche à l'écran les k premiers termes de la suite de Syracuse de N. -
Écrire une fonction
test_Syracuse(N,k)qui teste si l'un des k premiers termes de la suite de Syracuse de N vaut 1 (cette fonction doit retournerTruesi oui etFalsesinon).