TP 2
Sauts Conditionnels
Exercice 1: Simulation de grande aiguille
Écrire une fonction une_minute_en_plus(h,m) qui calcule l'heure une minute après celle passée en paramètre sous forme de deux entiers que l'on suppose cohérents. Voici quelques exemples :
-
une_minute_en_plus(14,32)renvoie (14,33) -
une_minute_en_plus(18,59)renvoie (19,0)
Ne pas oublier le cas de minuit.
Exercice 2: Résolution d'équations
- Écrire une fonction
afficher_solution_premier_degre(a,b)qui prend en paramètre deux réelsaetbet qui AFFICHE la solution de l'équationa.x + b = 0.Contrairement au TD, inclure le cas
a=0. On pourra afficher à l'écran des phrases comme"Pas de solutions"ou"Une infinité de solutions" - Écrire une fonction
afficher_solution_deuxieme_degre(a,b,c)qui prend en paramètre trois réelsa,betcqui AFFICHE la (les) solution(s) de l'équation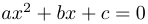 .
.
Ne pas oublier le cas
a=0. Penser à réutiliser la fonctionafficher_solution_premier_degre(a,b).
Exercice 3: Faute aux copies
La service de reprographie propose les photocopies avec le tarif suivant : les 10 premières coûtent 20 centimes l'unité, les 20 suivantes coûtent 15 centimes l'unité, et au-delà de 30 le coût est de 10 centimes. Écrire une fonction cout_photocopies(n) qui calcule le prix en euros à payer pour n photocopies.
Exercice 4: Découverte de la commande input
-
Tester la commande
input. On pourra jouer avec l'instruction suivante dans l'invite de commandes :t = input("Veuillez taper quelque chose...")Essayer de rentrer des réels, des flottants, n'importe quoi, des booléens, des chaînes de caractères, des variables... Que fait la commande
input ? - Quel est le danger d'utiliser une telle commande sur des programmes à accès public ?
Exercice 5: Application à la résolution d'équations du second degré
Utiliser la commande input pour écrire une fonction afficher_trinome() (sans argument), où l'on demandera poliment à l'utilisateur de taper 3 réels a, b et c et où l'on affichera la (les) solution(s) de l'équation 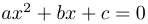 .
.
Les boucles
Exercice 6: Compter de 1 à n
Écrire une fonction compter_de_1_a(n) qui affiche les entiers d 1 à n.
Exercice 7: Puissances de 2
Écrire une fonction liste_puissances_2(n) qui affiche les n premières puissances de 2.
Exercice 8: Somme des cubes
Écrire une fonction somme_cubes(n) qui calcule 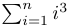 .
.
Exercice 9: Somme des factorielles
Écrire une fonction somme_factorielles(n) qui calcule 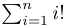 .
.
Exercice 10: Division euclidienne
Écrire deux fonctions qui calculent le quotient et le reste de la division euclidienne de deux entiers en utilisant uniquement les opérations d'addition et de soustraction.
Exercice 11: PGCD et PPCM
Écrire deux fonctions qui calculent le PGCD et le PPCM de deux entiers.
Exercice 12: Moyenne
Écrire une fonction qui demande à l'utilisateur de taper au clavier des réels et qui calcule et affiche au fur et à mesure la moyenne des réels qui ont été tapés. Le programme s'arrêtera dés que l'utilisateur entrera un nombre négatif.
Exercice 13: Quel est le nombre que j'ai en tête ?
Implémentez le jeu suivant:
Le joueur doit essayer de trouver un entier compris entre 1 et 100 que le programme tirera au hasard. (On utilisera le paquet random où se trouve la fonction randint(a,b) qui renvoie un entier au hasard entre a et b.)
Avant de commencer la partie, le joueur choisit un contrat c qui est le total d'essais qu'il est possible d'effectuer.
Une fois le contrat choisi, la partie commence. Le joueur a donc c propositions possibles.
A chaque proposition, l'ordinateur donne une indication en disant si la solution est plus petite ou plus grande que le nombre proposé par le joueur.
La partie se termine si le joueur a trouvé le nombre caché (il a gagné) ou s'il a utilisé toutes les propositions possibles (il a perdu).
Vous prendrez bien soin d'utiliser des fonctions pour rendre le code le plus lisible possible.