TP 3
Exercice 1: Fonctionnement des listes
Prévoyez le résultat que vous obtiendrez si vous exécutez le code suivant:
s = [0 , 0] t = s t[0] = 5 s[1] = 9 print( s ) print( t )
Exécutez ce code sur la machine et comparez avec ce que vous avez prédit. Si vous vous êtes trompé, essayer d'expliquer pourquoi.
Prévoyez le résultat que vous obtiendrez si vous exécutez les codes suivants:
import copy s = [0 , 0] t = copy.copy(s) t[0] = 5 s[1] = 9 print( s ) print( t )
import copy s = [[0,1] , [2,3]] t = s t[0][0] = 5 s[0][1] = 9 print( s ) print( t )
import copy s = [[0,1] , [2,3]] t = copy.copy(s) t[0][0] = 5 s[0][1] = 9 print( s ) print( t )
import copy s = [[0,1] , [2,3]] t = copy.deepcopy(s) t[0][0] = 5 s[0][1] = 9 print( s ) print( t )
Exécutez ce code sur la machine et comparez avec ce que vous avez prédit. Que fait copy et deepcopy ?
Exercice 2: Le miroir
Écrire un programme qui renverse tous les éléments d'un tableau T passé en paramètre.
Écrire un programme qui prend en paramètre un tableau T et qui renvoie un nouveau tableau qui est le miroir de T.
Exercice 3: Boîte à outils
Dans cet exercice, vous allez écrire des fonctions qui seront réutilisées plus tard dans d'autres exercices et d'autres TPs.
-
Tapez le programme suivant:
def demander_un_entier(): while True : try: return int( raw_input( "Veuillez donner un entier: " ) ) except ValueError: print "Vous n'avez pas donné un entier." entier = demander_un_entier() print entierTestez le programme. Que fait ce programme ? Sachant que la fonction
floatconvertit une chaîne de caractères en un réel, écrivez une fonctiondemander_un_reel(). -
Dans la paquet
random, il y a une fonctionrandint(a,b)qui prend en paramètres deux entiersaetbet qui renvoie un entier au hasard compris entreaetb.Écrire une fonction qui prend trois entiers
a,betnen paramètres et qui retourne un tableau contenantnentiers au hasard compris entreaetb.Écrire une fonction qui prend un entier
net deux réelsaetben paramètres et qui retourne un tableau contenant n réels compris entreaetb. -
Créez un module
utildans lequel vous enregistrerez toutes les fonctions de l'exercice.
Exercice 4: Moyenne
- Écrire un programme python qui prend une liste de réels en paramètres et qui renvoie la moyenne de ces entiers.
- Testez votre programme en utilisant des tableaux contenant des entiers aléatoires.
Exercice 5: Nombres premiers
-
Écrire une procédure
primalite(n), prenant en entrée un nombre entiern, et qui renvoie la valeurTrue(vrai) ouFalse(faux) selon que n est premier ou non. -
Écrire un programme qui prend en paramètre un entier
net qui renvoie sous forme de liste, lesnpremiers entiers premiers.
Exercice 6: Le crible Ératosthène
Le crible d'Ératosthène est un procédé qui permet de trouver tous les nombres premiers inférieurs à un certain entier naturel donné n. L'algorithme procède par élimination : il s'agit de supprimer d'une table des entiers de 2 à n tous les multiples d'un entier. En supprimant tous les multiples, à la fin il ne restera que les entiers qui ne sont multiples d'aucun entier, et qui sont donc les nombres premiers.
On commence par rayer les multiples de 2, puis à chaque fois on raye les multiples du plus petit entier restant.
On peut s'arrêter lorsque le carré du plus petit entier restant est supérieur au plus grand entier restant, car dans ce cas, tous les non-premiers ont déjà été rayés précédemment.
À la fin du processus, tous les entiers qui n'ont pas été rayés sont les nombres premiers inférieurs à n.
- Sur papier, appliquez le crible d'Ératosthène pour déterminer les nombres premiers inférieurs à 30.
-
Implémenter une fonction qui prend en paramètre un entier
net qui renvoie la liste des entiers inférieurs ànen utilisant le crible d'Ératosthène. Pour cela, vous utiliserez une listeLde taillen+1. Dans cette liste,L[i]vaudraTruesiiest un nombre premier,Falsesiin'est pas un nombre premier etNonesi l'algorithme n'a pas encore déterminé la primalité dei.
Exercice 7: Les nombres de Catalan
Les nombres de Catalan sont définis par la formule:
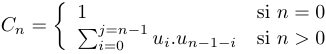
Écrire une fonction qui prend en paramètre un entier N et qui renvoie les N premiers nombres de Catalan.