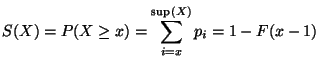Définition 1
Étant donné une expérience dont le résultat est aléatoire et soit
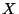
un
nombre associé au résultat de cette expérience. Supposons que
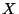
puisse
prendre les
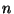
valeurs distinctes
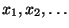
avec les
probabilités respectives
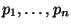
, on dit que
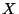
est une
variable aléatoire si :