


suivant: Détermination de
monter: Utilisation des probabilités conditionnelles
précédent: Un exemple ... ``plus
- -
- Considérons les évènements suivant :
- -
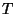 = ``le test est positif''
= ``le test est positif''
- -
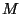 = ``le sujet est malade''
= ``le sujet est malade''
- -
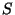 = ``le sujet est sain''
= ``le sujet est sain''
- -
- Remarquons :
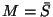 .
.
- -
- On recherche :
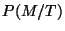 !
!
- -
- D'après l'énoncé, on connait les quantités suivantes :
D'après le théorème de Bayes:
Le problème se ramène donc au calcul de
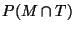 et de
et de 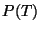 .
.
Pascal Ferraro
2002-11-22
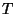 = ``le test est positif''
= ``le test est positif''
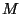 = ``le sujet est malade''
= ``le sujet est malade''
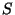 = ``le sujet est sain''
= ``le sujet est sain''
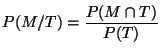
![]() et de
et de ![]() .
.