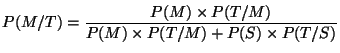suivant: Remarque 1
monter: Utilisation des probabilités conditionnelles
précédent: Détermination de
On peut remarquer que pour tout évènement:
où
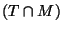 et
et
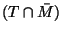 sont incompatibles:
De plus dans notre cas particulier:
sont incompatibles:
De plus dans notre cas particulier:
D'où:
On sait calculer
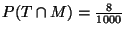 et d'après le théorème de Bayes:
et d'après le théorème de Bayes:
d'où finalement:
Pascal Ferraro
2002-11-22
![]() et d'après le théorème de Bayes:
et d'après le théorème de Bayes: