


suivant: Loi de Poisson
monter: Loi Hypergéométrique
précédent: Exemple d'application
- -
- Soit
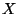 le nombre d'individus marqués parmi les
le nombre d'individus marqués parmi les 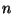 capturés.
capturés.
- -
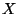 suit une loi hypergéométrique.
suit une loi hypergéométrique.
- -
- Idée, estimée
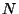 à partir des valeurs expérimentales de
à partir des valeurs expérimentales de 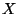 .
.
- -
- La méthode est appelée méthode de dilution ou de capture-recapture.
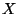 suit une loi hypergéométrique de parmètre
suit une loi hypergéométrique de parmètre 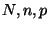 , d'où:
, d'où:
Expérimentalement on relève la valeur 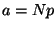 (ou
(ou 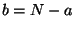 ) d'où :
) d'où :
On choisit 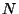 tel que
tel que 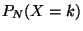 soit maximum (méthode du maximum
de vraissemblance).
soit maximum (méthode du maximum
de vraissemblance).
On considère le rapport :
En supposant qu'on a relevé 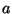 , alors pour calculer
, alors pour calculer 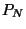 ,
, 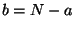 et pour calculer
et pour calculer 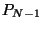 ,
, 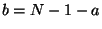 :
:
- -
- Le rapport
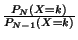 est
est 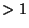 si
si
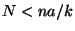 ;
;
- -
- Le rapport
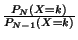 est
est 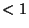 si
si
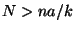 ;
;
- -
- d'où
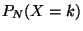 est maximal pour
est maximal pour 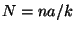 .
.
Application
Au cours d'une première capture on prélève 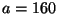 vairons que l'on
marque et relâche. Au cours de la seconde capture,
vairons que l'on
marque et relâche. Au cours de la seconde capture, 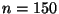 vairons
sont prélevés dont
vairons
sont prélevés dont 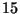 marqués. On estime donc à
marqués. On estime donc à
le nombre total de vairons.



suivant: Loi de Poisson
monter: Loi Hypergéométrique
précédent: Exemple d'application
Pascal Ferraro
2002-11-22
![]() suit une loi hypergéométrique de parmètre
suit une loi hypergéométrique de parmètre ![]() , d'où:
, d'où:
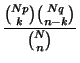
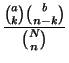
![]() tel que
tel que ![]() soit maximum (méthode du maximum
de vraissemblance).
soit maximum (méthode du maximum
de vraissemblance).
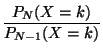
![]() , alors pour calculer
, alors pour calculer ![]() ,
, ![]() et pour calculer
et pour calculer ![]() ,
, ![]() :
:
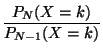
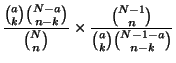
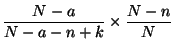
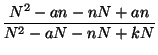
![]() vairons que l'on
marque et relâche. Au cours de la seconde capture,
vairons que l'on
marque et relâche. Au cours de la seconde capture, ![]() vairons
sont prélevés dont
vairons
sont prélevés dont ![]() marqués. On estime donc à
marqués. On estime donc à