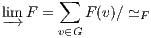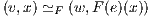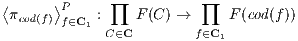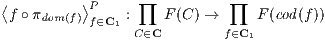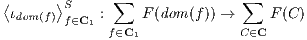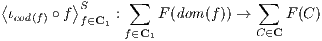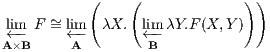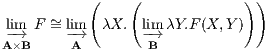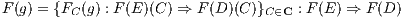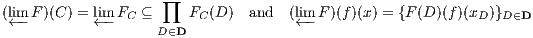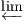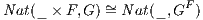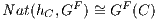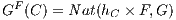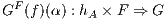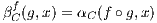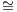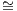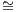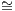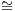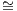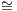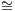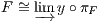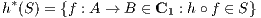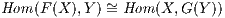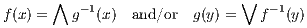Basics in category and topos theory
David Janin
UMR LaBRI, Bordeaux INP
Université de Bordeaux
janin@labri.fr
Ad hoc selection of elements of category and topos theory for a short series of lectures
at Bordeaux University graduate school (EDMI) in Mathematics and Computer Science.
Basic notions in posets and monoids are the mere requirement for such a lecture series.
1 Introduction
Categories where first defined by Eilenberg and Mac Lane in the 40s. It is said that Mac Lane wanted
to define natural transformations, therefore basic category theory should lay within the definitions
(and properties) of category themselves, functors and natural transformations. Everything else could
(should) be re-discovered by students ?
Of course many other mathematicians contributed to the theory. We may review in this lecture
further notions developed by Yoneda, Kan and Grothendieck. By lack of expertise in the field, we shall
give no historical references but, instead, invite the attendee to have a look at one of the following
book given as a (very short) selected bibliography:
- Barr and Wells [1], possibly smooth enough for computer scientists ,
- Mac Lane[4], the ultra-classic reference, a must be in one’s library,
- Mac Lane & Moerdijk[5], a classic reference on Sheaves and Topos theory,
- Johnstone [2], for the (very) courageous; 6 books in 3 volumes (only two printed yet) that
could be in Bordeaux Maths-Info library some day.
Aside many other books, other sources are available on the internet.
There is the fairly exhaustive Ncatlab website, for researchers in category theory, as well as various
category theoretic entries on Wikipedia. What is better ? To state it simply, Ncatlab is
complete but sometimes (very) hard to read as it offers many equivalent definitions for most
concepts. On the contrary, Wikipedia tells us what definitions buddies in the street actually
know.
Contents
2 Basics
2.1 Categories
Definition 2.1.1 (Category). A category C is defined by a collection of objects C0, a collection of
morphisms (also called arrows) C1 with domain and codomain functions dom,cod : C1 → C0, a
partial binary composition over C1 and identities idA ∈ C1, one for each A ∈ C0, such
that:
- g ∘ f is defined if and only if dom(g) = cod(f) with dom(g ∘ f) = dom(f) and
dom(g ∘ f) = dom(f) (compatibility)
- h ∘ (g ∘ f) = (h ∘ g) ∘ f whenever defined (associativity),
- f ∘ idA = f and idA ∘ g = gwhenever defined (local units),
for all f,g,h ∈,C1 and A ∈ C0.
Remark 2.1.2. Property (1) says that composition is defined on pairs of co-domain and
domain compatible functions. Property (2) says that composition is associative when defined.
Property (3) says that identities are local units for arrows.
Exercise 2.1.3. Prove that, for all A ∈ C0, the identity idA is the unique morphism such that
property (3) holds.
Notation 2.1.4. We may write A ∈ C for an object A ∈ C0 and f in C for a morphism
f ∈ C1. We may write f : A → CB (or simply f : A → B when there is no ambiguity) for
f ∈ C1 with dom(f) = A and cod(f) = B. The collection of morphisms from A to B, called a
homset, can be denoted by HomC(A,B) (or simply Hom(A,B) when there is no ambiguity) or
C[A,B].
Remark 2.1.5. The above axioms are depicted in Figure 1 by means of diagrams that are said to
commute.
In category theory, it is a general graphical tool to express function compositions equality by
means of diagrams, that is, directed graphs which vertices are labeled by objects of a category and
edges are labeled by arrows between these objects. A diagram is said to commute when every pair of
paths with same source and target define, by composing the functions they traverse, two equal
functions.
As there is always the cyclic empty path, implicitly labeled by an identity, the function induced by
any cyclic path necessarily equals the identity. Also, function defined by composing connected
edges does not need to be explicitly drown. In other words, the associativity and local unit
axioms are always assumed in a commuting diagram. In other words, the gray arrows in
Figure 1 are generally left implicit. See 2.3.4 and 4.1.1 for more about diagrams in category
theory.
Definition 2.1.6. A category C is small when both C0 and C1 are sets. The category C is
locally small when Hom(A,B) is a set for every pair of objects A,B ∈ C.
Remark 2.1.7. Unless stated otherwise, such as for the category Cat presented below, all
categories considered here are locally small.
Example 2.1.8. All notions listed below can be seen as certain type of categories. For each of them,
check what are objects, arrows and their composition, and check how the axioms defining these
notions relates to the category axioms.
- pre-ordered sets : categories with at most one arrow between any two objects,
- Posets: pre-ordered set with no cycle but identities,
- Monoid : categories with a single object,
- Groups : categories with a single objects and iso arrows only (see below),
- Groupoids : categories with iso arrows only (see below).
The term local units for identities come from semigroup theory.
Definition 2.1.9 (Isomorphisms). A morphism f : A → B in C is an isomorphism, or just
iso, when there is f-1 in C such that f ∘ f-1 = idB and f-1 ∘ f = idA. Two object A,B ∈ C
are called isomorphic, which is written A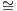 B when there is an isomorphism f : A → B in C.
B when there is an isomorphism f : A → B in C.
Exercise 2.1.10. Prove the unicity of inverse.
Example 2.1.11. Examples of locally small categories:
- Set with sets and functions,
- Poset with posets and monotonic functions,
- Monoid with monoids and morphisms.
2.2 Categories out of categories
Definition 2.2.1 (Product category). The product C × D of two categories C and D is
defined object-wise by taking (C × D)0 = C0 × D0 and (C × D)1 = C1 × D1 with
dom(f,g) = (dom(f),dom(g)), cod(f,g) = (cod(f),cod(g)) and (f,g) ∘ (f′,g′) = (f ∘f′,g ∘g′).
Exercise 2.2.2. Check that the product of two category is indeed a category. What is the
product of two monoids ? two groups ? two posets ?
Definition 2.2.3 (Opposite categories). Let C be a category. The opposite category Cop is
defined from C by exchanging dom and cod and reversing composition.
Exercise 2.2.4. What is the category (Cop)op ?
Exercise 2.2.5. What is the oppositie category of a monoid ? a group ? a poset ?
Remark 2.2.6. Remember (from college ?) that, in Set, function composition notation g∘f is
sort of reversed when thinking about the order of application. Some may prefer the sequential
notation f;g, i.e. apply f and then apply g. Formally, using the sequential composition notation
amounts to taking the opposite of the category Set. Of course, we do not expect functions in
Set to be reversible. This is just a notational convention.
Definition 2.2.7 (Slice category). Let C be a category and A ∈ C. The slice category C∕A
induced by A is the category which objects are the arrows of C into A and which arrows from
f : B → A to g : C → A are the arrows h : B → C such that f = g ∘ h.
Exercise 2.2.8. Check that C∕A is a category.
Definition 2.2.9 (Co-slice category). Let C be a category and A ∈ C. The co-slice category
A\C induced by A is the category which objects are the arrows of C from A and which arrows
from f : A → B to g : A → C are the arrows h : B → C such that h ∘ f = g.
Exercise 2.2.10. Check that A\C is a category.
Definition 2.2.11 (Arrow category). Let C be a category. The arrow category C→ is the
category which objects are the arrows of C and which arrows from f : A → B to g : C → D
are the pairs of arrows (h : A → C,k : B → D) such that k ∘ f = h ∘ g.
Exercise 2.2.12. Check that C→ is a category.
Definition 2.2.13 (Twisted arrow category). Let C be a category. The twisted arrow category
TW(C) is the category which objects are the arrows of C and which arrows from f : A → B
to g : C → D are the pairs of arrows (h : C → A,k : C → D) such that f = k ∘ g ∘ h.
Exercise 2.2.14. Check that TW(C) is a category.
Remark 2.2.15. In most of the definition above there is an abuse of language quite common in
category theory that amounts to implicitly assume that the homsets are not necessarily disjoints,
but instead, domain and codomain information are implicitly added to arrows whenever needed.
For instance, in the slice category C∕A, saying that h is an arrow from f to g whenever
f = g ∘ h actually mean that the triple (h,f,g) is the arrow induced by h in C∕A from f to
g. Indeed, the same arrow h in C may also induce other arrows, possibly distinct, each of the
form (h,f′,g′) in C∕B whenever f′ = g′∘ h.
Remark 2.2.16. Mathematicians seem to commonly think that arrows are “going down” as in
Figure 2 above. The slice category C∕A is thus often called the category of objects of C above
A. Similarly, especially in view of Figure 3 above, the co-slice category A\C is often called the
category of objects of C below A.
Of course, this is a convention, and, as a computer scientist, I confess that I tend to think
that arrows are “going up” as time is passing. A physicist may disagree thinking of passing time
as a phenomenon linked with gravity thus “going down” as well !
Exercise* 2.2.17. The sequential composition notation f;g looks like C programing doesn’t
it ? Shall C semantics also be defined by mean of a category ? Think of a C block semantics as
a function acting on the memory of the computer with designated variables “in-use”. Translate
program constructs (if, else, while-do, do-while, etc…) into semantics function compositions.
This looks like a compiler doesn’t it ? Eventually forget about C and use OCaml or Haskell
instead.
2.3 Graphs vs categories
Definition 2.3.1 (Graphs). A directed graph G is a quadruple G = ⟨V,E,sr,tg : E → V ⟩
with set of vertices V , set of edges E and source/target functions sr,tg : E → V .
Let G1 = ⟨V 1,E1,sr,tg : E1 → V 1⟩ and G2 = ⟨V 2,E2,sr,tg : E2 → V 2⟩ be two graphs. A
graph morphism φ : G1 → G2 is a pair of function φ0 : V 1 → V 2 and φ1 : E1 → E2 such that
preserves sources and targets, i.e. sr ∘ φ1 = φ0 ∘ sr and tg ∘ φ1 = φ0 ∘ tg.
Remark 2.3.2 (Type coherence). In the definition above, as in many other places throughout,
we may use the same function name for two functions which are unambiguously distinguished
by their domain and codomain, i.e. their type. For instance, in the equation sr ∘ φ1 = φ0 ∘ sr
given above, the left occurence of sr is necessarily the one of graph G2 and the right occurence
of sr is necessarily the one of graph G1, in order to ensure the type coherence with φ1 and φ0.
Exercise 2.3.3. Proves that graphs and graphs morphisms form a category Graph.
Definition 2.3.4 (Path categories generated graphs). The path category generated by G is the
category Path(G) with object V and which arrows the set of paths in G inductively defined
by:
- (s,ϵ,s) is a path (empty path on s),
- if sr(e) = s and tg(e) = t then (s,e,t) is a path (one-edge path),
- if (s,w,t) and (s′,w′,t′) are paths then (s,ww′,t′) is a path (path composition),
for all vertex s ∈ V , all edge e ∈ E and all (s,w,t),(s′,w′,t′) ∈ V × E*× V with E* the free monoid of
strings over E.
Exercise 2.3.5. Explicit the domain and co-domain functions in a path category Path(G) and
check that all category axioms are indeed satisfied.
Example 2.3.6. The category 0 generated by the empty graph, the category 1 generarated
by the one vertex graph, the category 2 generarated by the two vertices, one edge graph, the
category 3 generarated by the three vertices, two edges acyclic linear graph, etc…, see Figure 6.
Notation 2.3.7. By analogy with the category it induces, we shall simply write v ∈ G for a
vertex v ∈ V of the graph G and e : v → w in G for an edge e ∈ E of the graph G with
sr(e) = v and tg(e) = w.
2.4 Mono and epimorphisms
Definition 2.4.1 (Monomorphisms). An arrow f in C is an monomorphism, or just mono,
when for all g,h such that f ∘ g = f ∘ h we necessarily have g = h.
Exercise 2.4.2. Prove that monos in Set are the injective functions.
Definition 2.4.3 (Epimorphisms). An arrow f in C is an epimorphism, or just epi, when for
all g,h such that g ∘ f = h ∘ f we necessarily have g = h.
Exercise 2.4.4. Prove that monos in Set are the surjective functions.
Exercise 2.4.5. Prove that every iso is both a mono and an epi. Find the simplest category
into which the converse is false. Hint: think of path categories over a graph.
Remark 2.4.6. Monos and epis are the most general translations in category theory of the
notion of injections and surjections in Set. There are more restrictive ones. This often give the
feeling that category theory is complex.
But don’t bother. If ever you need such a more restrictive notion, define it yourself, use it
to check it is what you need, and eventually check what existing one it corresponds to, as it is
very likely it has been defined already.
2.5 Functors
Functors are to categories what morphisms are to algebras.
Definition 2.5.1 (Functors). A functor F : C → D is defined as a pair of functions F0 : C0 → D0
and F1 : C1 → D1 such that:
- F(f) : F(A) → F(B), i.e. dom and codomain preservation,
- F(idA) = idF(A), i.e. identities preservation,
- F(g ∘ f) = F(g) ∘ F(f), i.e. composition preservation,
for all A,B,C ∈ C, f : A → B and g : B → C in C.
Exercise 2.5.2. Prove that the direct image of an iso is an iso.
Exercise 2.5.3. Define the category Cat of (locally smal) categories and functors. Check that
the category axioms are satisfied. Is Cat locally small ?
Exercise 2.5.4. What does it mean that two (locally small) categories are isomorphic ?
Exercise 2.5.5. What are the functors between monoids, groups (use 2.5.2), posets, path
categories ?
Example 2.5.6. Examples of functors over Set ?
Definition 2.5.7. A functor F : C → D is faithfull when any two distinct arrows f,g : A →
CB are mapped to distinct arrows F(f),F(g) : F(A) → DF(B), i.e. the restriction of F to
HomC(A,B) is injective for all A,B ∈ C.
A functor F : C → D is full when for every arrows h : F(A) →DF(B) there is an arrow
f : A →CB such that F(f) = f, i.e. the restriction of F to HomC(A,B) is surjective for all
A,B ∈ C.
Exercise 2.5.8. Prove that Path, seen as a function from graphs into (small) categories, can
be extended into a functor from Graph into Cat. Is such a functor full ? Faithfull ?
Exercise 2.5.9. Given a sub-collection D0 ⊆ C0 of objects of a category C, how to define a
category from D0 ? How to extend the inclusion function from D0 into C0 into a functor. Is
this functor faithfull ? Full ? Define the notion of a subcategories and full subcategories.
Remark 2.5.10. Let C be a locally small category. There is the functor incC : C → Set by
incC(A) = {A} for all A ∈ C and incC(f) = A B for every f : A → B in C. In other words,
every locally small category is isomorphic to a (full) sub-category of Set.
B for every f : A → B in C. In other words,
every locally small category is isomorphic to a (full) sub-category of Set.
Exercise 2.5.11. Given a functor f : C → D in Cat, check that f is also a functor
f : Cop → Dop.
Definition 2.5.12 (Covariant vs contravariant functors). A functor f : C → D is called
covariant. A functor f : Cop → D (equivalently f : C → Dop) is called a contravariant functor
f : C → D.
Exercise 2.5.13. What are contravariant functors between monoids ? between posets ?
Exercise 2.5.14. Show that ()op can be extended into a covariant functor over Cat.
Equivalently, proves that any functor F : C → D can also be seen as a functor F : Cop → Dop.
2.6 Presheaves
Definition 2.6.1. Let C be a (locally small) category. A functor F : Cop → Set is called a
presheaf on C.
Exercise 2.6.2. What existing algebraic notion corresponds to a presheaf over a monoid ? a
group ?
Exercise* 2.6.3 (Presheaves on posets). Let F : Top → P be a presheaf over a poset T.
Define P = ⋃
t∈T{t}× F(t). Define (u,x) ≤ (v,y) when u ≤ v and x = F(u ≤ v)(y) for all
(tu,x),(v,y) ∈ P. Show that ≤ is a partial order relation over P. What functor properties
guaranty reflexivity and transitivity ? What property guarantee anti-symmetry ?
Let π : P → T defined by π(t,x) = x for all (t,x) ∈ P. Check that π is monotonic therefore
a poset functor. Prove that for all u ≤ v and y ∈ P such that π(y) = v there is a unique x ∈ P
such that x ≤ y and π(x) = u. Such a kind of functor is called a discrete fibration. See 3.3.2
for a generalization of this construction.
2.7 Homfunctors
Exercise 2.7.1. Let A ∈ C. Extend λY.Hom(A,Y ) into a covariant functor from C into Set.
Remark 2.7.2. The functor induced by λY.Hom(A,Y ) is often denoted by Hom(A, _). The
function induced by h : B → C from Hom(A,C) into Hom(A,B) that maps every f : A → B
to h ∘ f is denoted by Hom(A,f) or, more simply, by h ∘ _.
Exercise 2.7.3. Let B ∈ C. Extend λX.Hom(X,B) into a contravariant functor from C
into Set.
Remark 2.7.4. The functor induced by λX.Hom(X,B) is often denoted by Hom(_,B). The
function induced by h : A → C from Hom(C,B) into Hom(A,B) that maps every g : C → B
to g ∘ h : A → B is denoted by Hom(f,B) or, more simply, by _ ∘ h.
Exercise 2.7.5. Prove that λ(X,Y ).Hom(X,Y ) can be extended into a functor from Cop ×C
into Set.
3 Natural transformations
3.1 Natural transformations
Definition 3.1.1. Let F,G : C → D be two functors. A natural transformation α from F to
G, denoted by α : F ⇒ G, is a collection of functions αA : F(A) →DG(A), one for each A ∈ C,
such that, for every arrow f : A →CB we have G(f) ∘ αA = αB ∘ F(f).
The collection of natural transformation from F into G is denoted by Nat(F,G).
Definition 3.1.2 (Vertical composition). Let F,G,H : C → D. Let α : F ⇒ G and
β : G → H be natural transformations. The (vertical) composition β ∘ α of α and β is defined
by (β ∘ α)A = βF(A) ∘ αA for all A ∈ F.
Exercise 3.1.3. Proves that β ∘ α : F ⇒ H is a natural transformation. For such a purpose,
draw all the necessary commuting diagrams.
3.2 Functor categories
Definition 3.2.1 (Functor category). The collection Func(C,D) of functors from C into D
with natural transformation (composed vertically) is a category called the functor category.
This functor category is sometimes also denoted by [C,D].
Exercise 3.2.2. Prove that Func(C,D) is a category. For such a purpose, prove with
commuting diagrams that the (vertical) composition is associative and check what are its
identities.
Exercise* 3.2.3. What are the mono, epi and iso in the functor category Func(C,D) ?
Definition 3.2.4 (Equivalence of categories). Let C and D be two categories. We say that C
and D are equivalent, which is denoted by C ≃ D when there are two functors F : C → D and
G : D → C such that G ∘ F IdC in the functor category Func(C,C) and F ∘ G
IdC in the functor category Func(C,C) and F ∘ G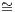 IdD in the
functor category Func(D,D).
IdD in the
functor category Func(D,D).
3.3 Discrete fibrations, presheaves and their element categories
Remark 3.3.1. As a special case of a functor category, there is the category Func(Cop,Set) of
presheaves on C and natural transformation between them. This category is generally denoted
by Psh(C) or  .
.
Definition 3.3.2 (Element categories of presheaves). Let C be a small category and F :
Cop → Set be a presheaf. The category of element of F, denoted by El(F), is defined by the
collection of object
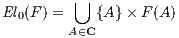
the collection of arrows
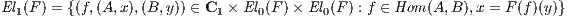
with
composition, identities, domain and codomain defined by:
- (f,(A,x),(B,y)) ∘ (g,(A′,x′),(B′,y′)) = (g ∘ f,(A,x),(B′,y′)) when (B,y) = (A′,x′),
- (idA,(A,x),(A,x)) with A ∈ C and x ∈ F(A),
- dom(f,(A,x),(B,y)) = (A,x) and cod(f,(A,x),(B,y)) = (B,y),
for all arrows (f,(A,x),(B,y)) and (g,(A′,x′),(B′,y′) in El(F).
Exercise 3.3.3. What is the element category of the inclusion functor inc : Cop → Set of Cop
into Set (see 2.5.10) ?
Exercise 3.3.4. Show that the element category El(F) of a presheaf F on a poset T is a poset.
Exercise 3.3.5. What is the element category of a presheaf on a monoid ? A group ?
Exercise 3.3.6. What is the element category of a presheaf on (the path category of) a graph ?
Exercise 3.3.7. Prove that El(F) is indeed a category. The projection of the element category
El(F) is defined by π : El(F) → C by π(A,x) = A for all object (A,x) ∈ El(F) and
π(f,(A,x),(B,y)) = f for all arrow (f,(A,x),(B,y)) in El(F). Prove that π is a functor.
Prove π satisfies the additional property that for all Y ∈ El(F) and f : A → π(Y ) in C
there is a unique X ∈ El(F) and arrow h : X → Y such that π(X) = A and π(h) = f.
Remark 3.3.8. The element category of a functor G : C → Set can be defined similarly,
though reversing its arrows. The resulting projection is then what is known in category theory
as an opfibration.
The projection of the element category of a presheaf is a fibration, a notion formalized
below.
Definition 3.3.9 (Discrete fibration). Let C and D be two small categories. A functor F :
D → C is called a (discrete) fibration when for every Y ∈ D for every f : A → F(Y ) in C there
is a unique X ∈ D and h : X → Y in D such that F(X) = A and F(h) = f.
Exercise 3.3.10. Prove that for every fibration F : D → C there is a presheaf G : Cop → Set
such that D is isomorphic to El(G) with F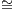 π.
π.
Remark 3.3.11. The presheaf deriving from a fibration F could be denoted by F-1. Then
Exercices 3.3.7 and 3.3.10 suggest that fibrations and presheaves are equivalent notions.
Such an intuition can be turned into a categorical equivalence. We examine below the
somewhat more explicit case of the category of element categories of presheaves on C.
Exercise 3.3.12. What is the element category of Hom(A, _) ? What is the element category
of Hom(_,B) ?
Exercise* 3.3.13. Let F,G : Cop → Set be two presheaves on C a poset and let El(F) and
El(G) be their element categories.
Let α : F ⇒ G be a natural transformation. Let θα : El(F) → El(G) defined for every
(u,x) ∈ El(F) by θα(u,x) = (u,αu(x)) and by θα(f,(u,x),(v,y)) = (f,(u,αu(x)),(v,αv(y)))
for all arrows (f,(u,x),(v,y)) in El(F). Prove that θα is a well defined functor that preserve
the projection, i.e. π ∘ θα = π.
Conversely, let θ : El(F) → El(G) be a functor that preserves π. Proves that there is a
unique natural transformation α : F ⇒ G such that θ = θα.
Exercise 3.3.14. Deduce from the above that the category FibD(C) of discrete fibrations over
C and projection preserving functors is equivalent to the category Psh(C) of presheaves on C
and natural transformations.
Exercise* 3.3.15 (Yoneda embeddings). Prove that both
![op o op
Y = λY.Hom (_, Y) : C → [C ,Set] and Y = λX.Hom (X, _) : C → [C, Set]](full8x.png)
defines functors. Show that these functors are full and faithfull.
Remark 3.3.16. Observe that the identity IdC : C → C is a fibration therefore C is indeed
(isomorphic to) the element category El(IdC). To which extent this reformulates Yoneda
embedding above within the category El(C) of element category of functor on the category C
(or the category Fib(C) of fibration – as defined above – to C).
3.4 Composing natural transformations and functors
Definition 3.4.1 (Horizontal composition). Let F,G : A → B and H,K : B → C. Let
α : F ⇒ G and β : H → K be two natural transformation. The horizontal composition β ⋆ α is
defined by (β ⋆ α)A = βF(A) ∘ αA for every A ∈ A.
Exercise 3.4.2. Prove that β ⋆ α is indeed a natural transformation β ⋆ α : H ∘ F ⇒ K ∘ G.
For such a purpose, draw all the necessary commuting diagrams. Check that the horizontal
composition is associative.
Exercise 3.4.3 (Mixed composition). How behaves the horizontal and vertical compositions
of natural transformations when one of the natural transformation is the identity ? In the
horizontal case, show it induces a left (or right) composition/action of a functor on a natural
transformation.
With F : A → B, G,H : B → C with α : G ⇒ H and K : C → D we may write
αF : G ∘ F ⇒ H ∘ F, Kα : K ∘ G ⇒ K ∘ H and KαF : K ∘ G ∘ F ⇒ K ∘ H ∘ F for such
compositions.
Remark 3.4.4. This mixed composition eventually leads to an example of a higher order
category that goes out of the scope of the present “basics”.
4 Diagram, limits and representations
4.1 Diagrams
Definition 4.1.1 (diagram). Let C be a category and G a graph with associated path category
Path(G). A diagram is a functor F : Path(G) → C.
Exercise 4.1.2. Check that a diagram is fully determined by the images of the vertices and
the arrows (one arrow path) of G. In other words, a diagram can simply be defined as a labeling
of G, its vertices by objects, its edges by (well-typed) arrows.
Definition 4.1.3 (Commutation property). A diagram F : Path(G) → C is a commuting
diagram when for every pair of paths p1,p2 in Path(G) we have F(p1) = F(p2).
Exercise 4.1.4. Check that, as already mentioned, every composition of functions along a
cycle from a vertex in a commuting necessarily equals the identity on the label of that vertex.
Exercise* 4.1.5. Let G1,G2,G be three graphs and let φ1 : G1 → G and φ2 : G2 → G
be two graph morphisms. Let H1 : Path(G1) → Path(G) and H2 : Path(G2) → Path(G)
be the two induced functors, i.e. H1 = Path(φ1) and H2 = Path(φ2) (see 2.5.8). Let
F1 : Path(G1) → C and F2 : Path(G2) → C be two commuting diagrams. Assume there is a
diagram F : Path(G) → C such that F1 = F ∘ H1 and F2 = F ∘ H2 as depicted in Figure 13.
Under which (sufficient) conditions the diagram F commute ? Are these conditions necessary ?
4.2 Constant diagram, cones and natural transformations
Definition 4.2.1 (Constant diagram). Let G be a graph and C be a category. Let X ∈ C. The
constant diagram ΔX : Path(G) → C is the diagram induced by ΔX(v) = X and ΔX(e) = idX
for all v ∈ G and e in G.
Definition 4.2.2 (Cones). Let G be a graph. Let F : Path(G) → C be a diagram. A cone on
F is an object X ∈ C and a collection of arrow αv : X → Xv in C, one for each v ∈ G such
that αw = F(e) ∘ αv for all e : v → w in G.
Exercise 4.2.3. Prove that there is a bijection between cone from X ∈ C to F and natural
transformation from ΔX to F.
Definition 4.2.4 (Co-cones). Let G be a graph. Let F : Path(G) → C be a diagram. A
co-cone on F is an object X ∈ C and a collection of arrow αv : Xv → X in C, one for each
v ∈ G, such that αv = αw ∘ F(e) for all e : v → w in G.
Exercise 4.2.5. Prove that there is a bijection between co-cones from F to X ∈ C and natural
transformations from F to ΔX.
4.3 Representable functors
Exercise 4.3.2. Under which condition the empty functor that maps every object to the empty
set and every arrow to the empty arrow is representable as a contravariant functor Hom(_,B)
or as a covariant functor Hom(A, _).
Exercise 4.3.3. Prove that the functor Hom(_ × Y,Z) : Set → Set is representable for any
choice of sets Y and Z.
4.4 Limits and colimits
Definition 4.4.1 (Limit). The limit of a diagram F : G → C, when it exists, is a
representation
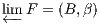
for the (contravariant) functor
Nat(Delta_
,F), i.e.
Nat(Δ_
,F) ≡ Hom(_
,B) via
β. By abuse
of notation, the object
B is often denoted by
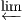 F
F.
Definition 4.4.2 (Colimit). The colimit of a diagram F : G → C, when it exists, is a
representation
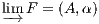
for the (covariant) functor
Nat(F,Delta_
), i.e.
Nat(F,Δ_
,F) ≡ Hom(A, _
) via
α. By abuse
of notation, the object
A is often denoted by
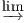 F
F.
Exercise 4.4.3 (Typical limit/colimit shapes). Examine the limits (or the colimits) of diagram on
the following graphs:
- Terminal/initial object (empty graph),
- Trivial limit/colimit (one isolated vertex, one edge and its two vertices),
- Categorical product/co-product (two isolated vertices),
- Equalizer/co-equalizer (two edges with same source and target),
- Pullback/trivial colimit (two edges with same target),
- Trivial limit/pushout (two edges with same source).
Rephrase each of the above notions in terms of the existence of certain cones/co-cones (object and
arrows) that are universal/co-universal for the corresponding classes of cones/co-cones, i.e. through
which these cones/co-cones uniquely factorizes.
Exercise* 4.4.4. Rephrase the general definition of limits (colimits) in terms of the existence
of certain cone (co-cone) through which every other cone (co-cone) factorizes.
Exercise 4.4.5 (Limit in Set). Let F : G → Set be a diagram. Prove that, we have
![{ }
∏
l←im- F = x ∈ F(v) : ∀e : v → w ∈ G1, x[w ] = F(e)(x[v])
v∈G](full17x.png)
where
x[v] denotes the
vth component of an element
x ∈∏
v∈GF(v).
Exercise* 4.4.6. Generalize the above by proving that a category C that has all (small/finite)
products and equalizers has all (small/finite) limits.
Exercise 4.4.7. With F : G → Set, examine the validity of the following assertion:
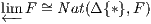
Exercise 4.4.8 (Colimit in Set). Let F : G → Set be a diagram. Prove that, we have
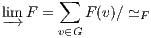
where
∑
v∈GF(v) = ⋃
v∈G{v}× F(v) is the disjoint sum of the images of the vertices by
F,
and
≃F is the least equivalence relation over this disjoint sum such that
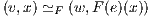
for all edges
e : v → w in
G and element
x ∈ F(v).
Remark 4.4.9. Observe the analogy between the disjoint sum definition and the element
category construction on a covariant functor. Observe that the equivalence defined above is sort
of a categorical congruence (the least one) with respect to the (forward image) arrows of the
element category.
Exercise 4.4.10 (Limit from products and equalizers). Let F : C → D with small C. Prove
that, when it exists, the limit of F is the equalizer of the following two functors:
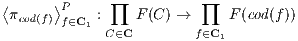
and
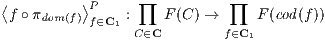
where
⟨fi : A → Ai⟩P is the unique arrow from
A into
∏
iAi through which the collection of
arrows
{fi : A → Ai}i factorizes. This generalizes the
parallel application of set functions from
the same set.
Exercise 4.4.11 (Co-limit from co-products and co-equalizers). Let F : C → D with small
C. Prove that, when it exists, the co-limit of F is the co-equalizer of the following two functors:
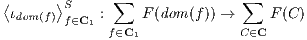
and
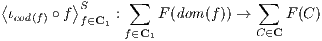
where
⟨fi : Ai → A⟩S is the unique arrow from
∑
iAi into
A through which the collection
of arrows
{fi : Ai → A}i factorizes. This generalizes the
alternative application of a set of
functions from the sum of their domain.
Exercise 4.4.12 (Parametrized limit and colimit). Prove that, given F : A×B → C, we have
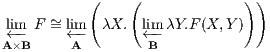
and
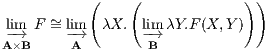
for small
A and
B.
Exercise 4.4.13 (Limits on presheaves). Prove that the category Psh(C) of presheaves on C
and natural transformation has all small limits and colimits, i.e. limits and colimits over diagram
of the form G → Psh(C) for small graphs.
Hint: limits/colimits over presheaves can be computed object-wise. More precisely, given
F : D → (Cop → Set) a diagram on Psh(C), for every C ∈ C, let FC : D → Set be the
diagram on Set defined by FC(D) = F(D)(C) and, for every g : D → E in D, FC(g) defined
as the Cth component of the natural transformation
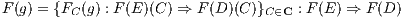
Check that
FC : D → Set is indeed a functor. Define then
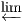 F
F to be the presheaf given by
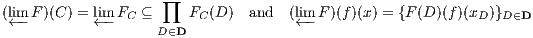
for every
f : A → B and every
x = {xD ∈ FB(D)}D∈D ∈ FB
FB. Check that
 F
F is indeed
a presheaf and the limit via the natural transformation given by the projections
{πD}D∈D as
depicted in Figure
16.
In Figure 16 we also depict another cone from (H,α) to F with α = {αD : H ⇒ F(D)}D∈D and, for
every D ∈ D, αD = {αDC : H(C) → F(D)(C)}C∈C.
4.5 Exponent in cartesian category
Let C be a cartesian category, that is, a category that has a terminal object 1 and binary categorical
products A × B for all A,B ∈ C.
Exercise 4.5.1. Given f : X → Y and g : X′ → Y ′ show that there is a unique arrow
f × g : X × X′ → Y × Y ′ through which f ∘ π1 : X × X′ → Y and g ∘ π2 : X × X′ → Y ′
factorizes via Y × Y ′, i.e. f ∘ π1 = π1 ∘ f × g and g ∘ π1 = π2 ∘ ftimesg.
Definition 4.5.2. Let C be a cartesian category and B,C ∈ C. The exponent of C by B in C
is a object CB ∈ C and a natural isomorphism α : Hom(_ × B,C) Hom(_,CB).
Hom(_,CB).
When the cartesian category C has all exponent, we say that C is a cartesian closed category.
Exercise 4.5.3. Let P be a poset seen as a category. Prove that for all a,b,c ∈ P we
have:
- the terminal element of P is its maximum element 1,
- the product of a,b ∈ P is the meet a ∧ b,
- if it exists, the exponent cb equals ∨
{x ∈ P : x ∧ b ≤ c},
Exercise 4.5.4. Let P be a bi-cartesian closed poset, that is, a cartesian closed poset that also has
an initial element and all co-product. Prove that for all a,b,c ∈ P we have:
- the initial element of P is its minimum element 0,
- the co-product of a,b ∈ P is the join a ∨ b,
- a ∧ (b ∨ c) = (a ∧ c) ∨ (b ∧ c),
- a ∨ (b ∧ c) = (a ∨ c) ∧ (b ∨ c).
Remark 4.5.5. Bi-cartesian closed poset P as above are known in the literature as a Heyting
Algebra. This notion plays a fundamental role in logic, especially because of the (intuitionistic)
negation defined by ¬a = 0a. Such a negation does not need to be idempotent. Such a notion
also arises in topology as quickly detailed below.
Assume that P is the poset of open sets on a topological space X ordered by inclusion.
These open sets indeed form a Heyting algebra with finite intersection as meet and arbitrary
union as join. Then, the “negation” of every open x ∈ P can be defined as the interior of its
complement, that is, the greatest open set included into its complement.
Observe that such a topological intuition can also be dualized by considering instead the
poset of closed subsets of X ordered by reverse inclusion with finite union as meet and arbitrary
intersection as join. In this case, the “negation” of a closed set is the closure of its complement,
that is, the least closed subset that contains its complement.
Exercise 4.5.6. Assume that the exponent (CB,α) is defined. Prove that there exists an arrow
eval : CB × B → C such that, for all f : A × B × C there is a unique arrow f* : A → CB such
that eval ∘ (f*× idB) = f.
Hint : consider the naturality diagram of α-1 : Hom(_,CB) → Hom(_ × B,C) in Figure 17
and take eval = αCB-1(idCB) and f* = α(f).
We see that eval ∘ (f*× idB) = f and unicity follows from the fact that α therefore α-1 is
a natural isomorphism.
Exercise 4.5.7. Prove that in Set, the exponent CB = B → C, the set of function from B to
C, with eval(f,b) = f(b) for all f ∈ CB and b ∈ BC.
4.6 Yoneda Lemma
The notion of representation plays a key role for defining limits, colimits and exponent. Moreover,
the diagram chasing techniques used in Figure 17 is a particular case of a fairly general
technique for analyzing or proving representation facts. This technique is known as the Yoneda
lemma.
Lemma 4.6.1 (Yoneda). Let F : Cop → Set be a functor. Let B ∈ C be an object of C.
Then the function θ : Nat(Hom(_,B),F) → F(B) defined by θ(α) = αB(idB) for every
α : Hom(_,B) ⇒ F is a bijection natural in both B and F, i.e. Nat(Hom(_,B),F) and F(B)
are naturally isomorphic via θ.
Proof. Let α : Hom(_,B) ⇒ F. Let A ∈ C and h : A → B. This situation is depicted
Figure 18.
Injectivity. By definition of natural transformation, we have
αB(h∘idA) = F(h)(αA(idA)) that is
αA(h) = F(h)(θ(α)) for all
h : A → B in
C. As this holds for arbitrary
A ∈ C and
h ∈ Hom(A,B)
this means that
α is fully determined by
θ(α) therefore
θ is injective.
Surjectivity. Conversely, given
b ∈ F(B), there is the natural transformation
αb defined as the
collection of functions
{αAb : Hom(A,B) → F(A)}A∈C defined by
αAb(h) = F(h)(b) for all
A ∈ C and
h ∈ Hom(A,B). The fact it is a natural transformation immediately follows from the fact that
F
is a contravariant functor. Since, by definition, we have
θ(αb) = b this implies that
θ is
surjective.
To be completed. It remains to prove naturality in both
B and
F.
__
Exercise 4.6.2. (Re)prove, using Yoneda Lemma, that y : C → (Cop → Set) defined by
y(C) = Hom(_,C) is a full and faithfull embedding of C into Psh(C).
Exercise 4.6.3. Prove, using Yoneda lemma (see hint below), that the category Psh(C) of
presheaves on C and natural transformation is cartesian closed.
Hint, expanded from [3], p 170 : let F,G ∈ Psh(C). We look for a presheaf GF ∈ Psh(C) such
that
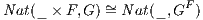
For every
C ∈ C there is the presheaf
hC = Hom(_
,C) and, by Yoneda Lemma, we have
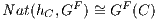
therefore, by combining the above equivalence, this suggest to define
GF by
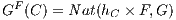
for every
C ∈ C. Then, for every
f : A → B, we need to define
GF(f) : GF(B) ⇒ GF(A) that
is,
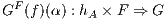
for every
α : hB × F ⇒ G. In order to simplify notation, clarity, let us write
βf = GF(f)(α).
For every C ∈ C we must have βCf : Hom(C,A) × F(C) ⇒ G(C) so, for every
g ∈ Hom(C,A) and x ∈ F(C) we simply put
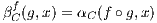
which is well typed since
f ∘ g : C → B.
Checking that its is indeed an exponential is left as exercise. The remark below give some
hints on how to proceed in proving the expected equivalence Nat(_×F,G)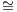 Nat(_,GF); just
follow the types !
Nat(_,GF); just
follow the types !
Remark 4.6.4. In the exercise above, we have defined GF(f) just by making a type analysis,
so that the available elements combine correctly, somehow regardless of what actually are these
elements. This is a typical type drive reasoning (aka proof) that plays a major role in type-driven
programing where the moto is: correctness by well-typeness ! A motto we just have followed in
this construction of the exponential in Psh(C).
5 Elementary topoi
We shall briefly survey the notion of topos that arises from the notion of presheaves and sheaves on a
Grothendieck site. There is a lot more to be said. The reader is invited to further reading. In this
presentation, we follow some elements of MacLane and Moerdijck [5].
5.1 Sub-objects
Let C be a category. Remember that f : A → B is a monomorphism when, for all C ∈ C, the function
f ∘ _ : Hom(C,A) → Hom(C,B) is injective .
Definition 5.1.1. Let f : B → A and g : C → A be two monos into A. Define f ≤ g when
there is h : B → C such that f = g ∘ h.
Exercise 5.1.2. Prove that h : B → C as above is necessarily a monomorphism. Prove that
the relation ≤ defined above is a pre-order, i.e. it is reflexive and transitive. The relation f ≃ g
defined when f ≤ g and g ≤ f is thus an equivalence relation.
Definition 5.1.3 (Subobjects). A subobject of A in C is the equivalence class of a mono
[f : B → A] under the above pre-order equivalence. The collection of subobject of an object A
is denoted by Sub(A).
Exercise 5.1.4 (Subobjects in Set). Show that the inclusion functions incX : X → Y for
every X ⊆ Y are canonical representatives of the subobjects (subset) of a set Y .
Exercise 5.1.5 (Subobjects in a poset). Let P be a poset. What are the monos in P ? Let
x ∈ P. What are the subobjects of x ∈ P ?
5.2 Subobject classifier
Definition 5.2.1 (Pullback). Let f : X → Z and g : Y → Z. The pullback of (f,g) is a pair of arrow
(f′ : X ×ZY → X,g′ : X ×ZY → Y ) such that every other pair (f′′ : Z′→ X,g′′ : Z′→ Y ) such that
f ∘ f′′ = g ∘ g′′ uniquely factorizes through (f′,g′).
Then we say that f′ is the pull back of g along f and g′ is the pullback of f along
g.
Exercise 5.2.2 (Subobject functor). Assume that C has all pullbacks. Let h : Y → X in C.
(1). Let f : Z → X be a monomorphism and let g : Y ×XZ → X the right part of a pullback
of (f,h), called the pullback of h along f. Prove that g is mono.
(2). Let f′ : Z′ → X be a monomorphism with f′ ≃ f as subobject. Prove that
g′ : Y ×XZ′→ X is the pullback of h along f′ if and only if g′≃ g as subobject.
(3). Deduce from the above that there is the well defined function Sub(h) : Sub(X) → Sub(Y )
that maps every subobject [f : Z → X] ∈ Sub(X) to [g : Y ×XZ → X] ∈ Sub(Y ) given by any
pullback g of h along f.
(4). Check that Sub(idX) = idSub(X) and Sub(h) ∘ Sub(h′) = Sub(h′∘ h) whenever h′∘ h
is defined, therefore, assuming that Sub(X) is a set for all X ∈ C, there is the contravariant
functor Sub : Cop → Set.
Definition 5.2.3. Assume that C has all pullbacks. A subobject classifier is an object Ω ∈ C
together with a natural isomorphism Sub(_)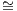 Hom(_,Ω).
Hom(_,Ω).
Exercise 5.2.4. Assume that C also has a terminal object 1.
(1). Assume a subobject classifier (Ω,α). Let true : 1 → Ω defined as α1(id1). Prove that
for all mono f : X → Y there is a unique Xf : Y → Ω such that f is the pullback of true along
Xf.
(2). Conversely, assume there is true : 1 → Ω such that for all mono f : X → Y there
is a unique Xf : Y → Ω such that f is the pullback of true : 1 → Ω along Xf : Y → Ω.
Check that if f′≃ f as a subobject then Xf′ = Xf. Deduce from the above that (Ω,{αX}X∈C)
is a subobject classifier with αX : Sub(X) → Hom(X,Ω) defined for every [f] ∈ Sub(X) by
αX([f]) = Xf.
Exercise 5.2.5. What is the subobject classifier in Set ?
Exercise 5.2.6. Is there a subobject classifier in a poset ? In the category Poset of posets and
monotone functions ?
Exercise 5.2.7. Prove that a natural transformation α : F → G between two presheaves
on C is mono/iso if and only if each of its component αC : F(C) → G(C) for C ∈ C is a
injection/bijection.
Definition 5.2.8 (Subfunctor). Let F,G : Cop → Set be two functors. We say that F is a
sub-functor of G, which is simply denoted by F ⊆ G, when:
- F(C) ⊆ G(C),
- F(f) is the restriction of G(f) to F(C),
for all objects C,D ∈ C and arrows f : C → D in C.
Exercise 5.2.9 (Subobjects in Psh(C)). Let F,G : Cop → Set. Check that F is a subfunctor
of G if and only if there is a injective (aka mono) natural transformation α : F ⇒ G. Deduce
that every subobject of G contains one and only one subfunctor.
Exercise 5.2.10. Prove, using Yoneda Lemma, that Psh(C) has a subobject classifier defined
by Ω(C) = {F ⊆ Hom(_,C)}, that is, the functor that maps every object C to the set of
subfunctor of the homset presheaf y(C) = Hom(_,C). In particular, what is the characteristic
function XF : G → Ω of any subfunctor F ⊆ G.
5.3 Power object
Let C be a category with all finite limit.
Definition 5.3.1. Let A ∈ C. A power object for A ∈ C is an object PA ∈ C and a natural
isomorphism α : Hom(A × _,Ω)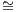 Hom(_,PA).
Hom(_,PA).
Exercise 5.3.2. What is the power object and the associated natural transformation in Set ?
Hint: remember that Ω = {0,1} therefore any function f : A × B → Ω uniquely determined a
relation Rf = f-1(1) ⊆ A×B. Observe that there are at least two (equivalent) possibilities for
defining α.
Remark 5.3.4. Let (ΩA,α) be the power-object of A ∈ C. By definition of subobject classifier
Ω, there is β : Sub(A× _)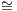 Hom(A× _,Omega) therefore α∘β : Sub(A× _)
Hom(A× _,Omega) therefore α∘β : Sub(A× _)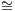 Hom(_,PA).
Hom(_,PA).
Exercise 5.3.5. Following the above remark, describe the power object in Set and the
associated natural transformation α ∘ β.
Hint : every relation (subobject) R ⊆ A × B defines a fonction fR : A → 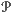 (B) defined by
fR(a) = {b ∈ B : (a,b) ∈ R.
(B) defined by
fR(a) = {b ∈ B : (a,b) ∈ R.
Exercise 5.3.6. Let (ΩA,α) be the power-object of A ∈ C. Let inA : A×PA → Ω defined by
inA = αPA(idPA)and let h :∈A → A × PA be the (right part of) the pullback of (inA,idΩ).
Prove that for every monomorphism f : R → A × B the morphism XR = α(Xf) : B → PA
is the unique morphism from B → PA such that, given g : A×B the unique morphism given by
the universality property of the pullback ∈A, the pair (f,g ∘ f) is the pullback of (id × XR,h)
as depicted in Figure 21.
Exercise 5.3.7. With the help of the previous exercise, prove that a power object for A can
equivalently be defined as an object ΩA ∈ C and a monomorphism ∈A → A×ΩA such that for
every object B ∈ C and monomorphism R → A×B there is a unique morphism XR : B → ΩA
such that R is the pullback depicted in Figure 22.
Exercise 5.3.8. What are the membership relations and characteristic functions of relations
in Set ?
Exercise 5.3.9. What are the power objects, the membership relations and characteristic
functions of relations in Poset ?
Exercise 5.3.10. What are the power objects, the membership relations and characteristic
functions of relations in a poset P ?
Exercise 5.3.11. What are the power objects, the membership relations and characteristic
functions of relations in Psh(C) ?
5.4 Elementary topos
Exercise 5.4.1. Assume that C has all finite limits and exponents and has a subobject
classifier Ω. Prove that for every A ∈ C, the subobject classifier ΩA is indeed the exponent of
Ω by A.
Exercise 5.4.2. Assume that C has all finite limits and power objects. Prove that Ω1 is a
subobject classifier and C is cartesian closed.
Definition 5.4.3. An elementary topos is a category C that has all finite limits and power
objects or, equivalently, that has all finite limits, exponents and subobject classifier.
Exercise 5.4.4. Check, from exercises above, that both Set and Psh(C) are elementary topoi.
Exercise* 5.4.5 (Co-completion of C). Prove that Psh(C) is co-complete, i.e. it has all small
co-limits. Let then F : Cop → Set. There is the element category El(F) equipped with the
(discrete fibration) projection functor πF : El(F) → C. Prove that:
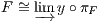
where
y : C → Psh(C) is the Yoneda embedding defined by
y(C) = Hom(_
,C) for every
C ∈ C.
More generally, prove that, for every functor A : C → D where D is co-complete and
locally-small, there is, up to isomorphism, a unique functor G : Psh(C) → D such that
G|y(C)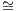 A, i.e. G restricted to the full and faithfull embedding of C into Psh(C) define by
y(C) is isomorphic to A.
A, i.e. G restricted to the full and faithfull embedding of C into Psh(C) define by
y(C) is isomorphic to A.
To which extent this says that y : C → Psh(C) is initial among functors from C into (locally
small ?) co-complete categories and colimit preserving functors ?
Hint: define G by G(F) = 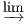 A ∘ πF for every F ∈ Psh(C).
A ∘ πF for every F ∈ Psh(C).
Remark 5.4.6. It is said (see [5]) that Yoneda defined the category of elements of a presheaf
(in order to prove such a result ?) before Grothendieck defined “his” construction that lifts
the category of elements construction to arbitrary functor F : C → Cat. This Grothendieck
construction, much related with the general notion of fibration, is reviewed at the end of these
notes (see [?] for many more details).
5.5 Grothendieck topologies
Let C be a small category.
Definition 5.5.1. A sieve S on C ∈ C is a is a “backward closed” collection of arrows of C to
C, i.e. for all g : B → C in S and f : A → B in C then g ∘ f : A → C in S.
Exercise 5.5.2. Check that a sieve over a poset P on x ∈ P is simply a downward closed
subset of P below x, i.e. y ≤ x for all y ∈ P.
Exercise 5.5.3. Check that every sieve S on C ∈ C can be seen as a subfunctor FS ⊆
Hom(_,C) by putting FS(A) = {f ∈ S : dom(f) = A} for every A ∈ C and FS(f) = _ ∘ f :
S(B) → S(A) for every f : A → B.
Conversely, prove that every subfunctor F ⊆ Hom(_,C) is uniquely determined by the set
SF = {f ∈ C1 : ∃A ∈ C,f ∈ S(A)} which is a sieve on C.
In other words, sieves on C and subfunctors of Hom(_,C) are equivalent notions.
Exercise 5.5.4 (Sieve functor). When S is a sieves on C and h : B → C is a morphism, prove
that
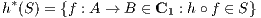
is a sieve on
B.
It follows that there is the functor
Sieve : Cop → Set that maps every object C ∈ C to the set of sieves on C and that maps every
h : A → B to the function over sieves h*.
Check that we indeed have id* = id and f*∘ g* = (g ∘ f)*.
Definition 5.5.5. Let C be a category and C ∈ C. A Grothendieck topology over C is an assignment
of a collection of sieves sieves J(C), one for each C ∈ C, such that:
- (maximality) the maximal sieve {f : A → C}∈ J(C),
- (stability) if S ∈ J(C) then h*(S) ∈ J(B) for all h : B → C,
- (transitivity) if S ∈ J(C) and R is any sieve on C such that h*(R) ∈ J(B) for all
h : B → C ∈ S, then R ∈ J(C).
A site is a pair (C,J) where J is a Grothendieck topology over C.
Exercise 5.5.6. Check that the following assignment are Grothendieck topologies:
- discrete topology: every sieves on C belongs to Jd(C),
- indiscrete topology: only the maximal sieves on C belongs to Ji(C).
Exercise* 5.5.7. We have already seen that sieves on x ∈ P for a poset P are the downward
closed subsets of P below x. A subset X ⊆ P is directed when X is non empty and for every
x,y ∈ X there is z ∈ X such that x,y ≤ z.
A set X ⊆ P is closed in the Scott topology when X is downward closed and for every
Y ⊆ X directed such that ∨
Y exists then ∨
Y ∈ X. Accordingly, the Scott-closure of a set
X ⊆ P is the least closed subset X ⊆ P such that X ⊆X.
Define for every x ∈ P the collection of sieves Js(x) to be the set of all downward closed
subset X ⊆ P such that X = ↓x, the downward closure of x.
Prove that Js is a Grothendieck topology.
Exercise 5.5.8. Let J be a Grothendieck topology. Check J induces a functor J : Cop → Set
that maps every object C ∈ C to the set of sieves J(C) on C and that maps every arrow
h : A → B in C to the arrow h* restricted to J(B) into J(A). Observe that Ji ⊆ J (by
maximality) and J ⊆ Jd (by stability) as subfunctors. Are there subfunctors of Jd (that we
also named Sieve above) that are not Grothendieck topologies ?
5.6 Sheaves
Definition 5.6.1 (Matching family). Let J be a topology on C and F : Cop → Set be a
presheaf. Let C ∈ C and S ∈ J(C) a sieve on C. A matching family for S on F is a collection
of element {xf ∈ F(A)}f:A→C∈S such that for all g : B → A and f : A → C ∈ S we have
xf∘g = F(g)(xf).
Exercise 5.6.2. We have seen that every sieves on C ∈ C can be seen as a subfunctor of
Hom(_,C). Check that matching families for S on F can equivalently be defined as natural
transformations S ⇒ F.
Definition 5.6.3 (Sheaf on a site). Let (C,J) be a site. A presheaf F : Cop → Set is a sheaf
for J when, for any object C ∈ C, any sieve S ∈ J(C), any matching family {xf}f∈S of F on
S there is a unique x ∈ F(C) such that xf = F(f)(x) for all f ∈ S. The element x is called the
amalgamation of the matching family {xf}f∈S.
Exercise 5.6.4. Check that every presheaf F : Cop → Set is a sheaf for the indiscrete topology
on C.
Exercise 5.6.5. Check that if F : Cop → Set is a sheaf for a topology J, then, for every C ∈ C
such that J(C) = ∅, we must have F(C) a singleton. Deduce that every sheaf F for the discrete
topology is, up to isomorphism, the constant sheaf Δ{*}.
Theorem 5.6.6. For any topology J on C, the category Sh(C,J) of sheaves for J and natural
transformation is an elementary topos.
Exercise 5.6.7. Consider proving the above theorem.
Remark 5.6.8. The converse is not true. A topos that is equivalent to some Sh(C,J) is called
a Grothendieck topos. Indeed, such a topos has all small limits and colimits which is not require
for an elementary topos.
6 Adjunction
6.1 Definition and examples
Definition 6.1.1. Let F : A → B and G : B → A. We say that F is the left adjoint of
G, equivalently G is the right adjoint of F, a property denoted by F ⊣ G when there is the
isomorphism
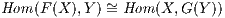
natural in both
X ∈ A and
Y ∈ B.
Exercise 6.1.2. Let P,Q be two posets, f : P → Q and g : Q → P two isotone functions, i.e.
morphisms in Poset. Proves that f ⊣ g if and only if
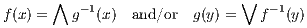
for all
x ∈ X and
y ∈ Y . In particular, the function
f (resp.
g) is uniquely defined by the
function
g (resp.
f).
Exercise 6.1.3. Prove that if F ⊣ G and F ⊣ G′ then G and G′ are naturally isomorphic. In
other words, a left adjoint F defines its right adjoint up to isomorphism.
Similarly, prove that if F ⊣ G and F′⊣ G then F and F′ are naturally isomorphic. In other
words, a right adjoint G defines its left adjoint up to isomorphism.
Exercise 6.1.4 (Unit and co-unit). Assume that F ⊣ G. Taking F(X) for Y yields a
isomorphism α : Hom(F(X),F(X))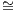 Hom(X,G∘F(X)). Prove that η : IdA ⇒ G∘F defined
by ηX = αX(idF(X)) : X → G ∘ F(X) for every X ∈ A is a natural transformation called the
unit of the adjunction F ⊣ G.
Hom(X,G∘F(X)). Prove that η : IdA ⇒ G∘F defined
by ηX = αX(idF(X)) : X → G ∘ F(X) for every X ∈ A is a natural transformation called the
unit of the adjunction F ⊣ G.
Taking instead G(Y ) for X yields a isomorphism β : Hom(F∘G(Y ),Y 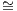 Hom(G(Y ),G(Y )).
Prove that ϵ : F ∘ G ⇒ IdB defined by ϵY = β-1(idG(Y )) : F ∘ G(Y ) → Y for every Y ∈ B is a
natural transformation called the co-unit of the adjunction F ⊣ G.
Hom(G(Y ),G(Y )).
Prove that ϵ : F ∘ G ⇒ IdB defined by ϵY = β-1(idG(Y )) : F ∘ G(Y ) → Y for every Y ∈ B is a
natural transformation called the co-unit of the adjunction F ⊣ G.
Check that Fη ∘ ϵF = IdF and ηG ∘ Gϵ = IdG (see mixed composition of functors and
natural transformations).
Exercise 6.1.5 (Adjunction by unit and co-unit). Let F : A → B and G : B ⇒ A. Prove
that if there are natural transformations η : IdA ⇒ G ∘ F and ϵ : F ∘ G ⇒ IdB such that
Fη ∘ ϵF = IdF and ηG ∘ Gϵ = IdG then we necessarily have F ⊢ G.
7 Further topics
7.1 Grothendieck construction
Definition 7.1.1 (Grothendieck construction). Let F : C → Cat be a functor. The Grothendieck
category C ⋉ F is defined with:
- objects: pairs of the form (A,X) such that A ∈ C and X ∈ F(A),
- arrows: pairs of the form (f,F) : (A,X) → (B,Y ) such that f : A → B in C and
F : F(f)(X) → Y in F(B),
with composition defined by (g,G) ∘ (f,F) = (g ∘ f,G ∘ F(g)(F)).
Remark 7.1.2. The soundness of this definition deserves a diagram that is depicted Figure 23.
Exercise 7.1.3. Check that in the case every F(A) is a discrete small category for all object
A ∈ C, i.e. a set equipped only element identities, and, therefore, F(f) is a set function for all
f in C, then C ⋉ F is the element category El(F) of F.
Exercise* 7.1.4. Study the categorical properties of the first projection π : C⋉F → C ? Give
sufficient conditions over a functor π : D → C for π-1 to induce a functor from C into Cat in
such way that D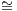 C ⋉ π-1. Are these conditions necessary ?
C ⋉ π-1. Are these conditions necessary ?
Exercise* 7.1.5. Recover the usual semi-direct product M ⋉ N of two monoids M and N via
an action α of M on N in terms of a Grothendieck construction of the form M ⋉ Fα for some
well chosen functor Fα : M → Cat.
References
[1] M. Barr and C. Wells. Category Theory for Computing Science, 3rd edition. Centre de
Recherche Mathématique (CRM), Montréal, 1999.
[2] P. Johnstone. Sketches of an Elephant: A Topos Theory Compendium, volume 43,44 of Oxford
Logic Guide. Oxford University Press, 2002.
[3] J. Lambek and P.J. Scott. Introduction to Higher-Order Categorical Logic. Cambridge Studies
in Advanced Mathematics. Cambridge University Press, 1988.
[4] S. Mac Lane. Categories for the Working Mathematician. Number 5 in Graduate Texts in
Mathematics. Springer, 1971.
[5] S. Mac Lane and I. Moerdijk. Sheaves in Geometry and Logic. Universitext. Springer, 1992.
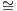
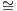


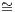
 .
.
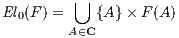
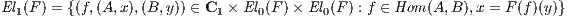
![op o op
Y = λY.Hom (_, Y) : C → [C ,Set] and Y = λX.Hom (X, _) : C → [C, Set]](full8x.png)
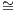
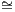
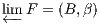
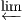
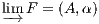
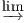
![{ }
∏
l←im- F = x ∈ F(v) : ∀e : v → w ∈ G1, x[w ] = F(e)(x[v])
v∈G](full17x.png)