Question de cours (6 points)
Parmi les algorithmes de tri de tableaux par Sélection, par insertion, à bulle, fusion vus en cours, quels sont ceux dont le résultat après une exécution partielle peut être interprété comme un tri partiel de tableau ? Justifier votre réponse en un maximum de 10 lignes.- Tri sélection - OUI : séquence initiale triée puisqu'on insère l'élément en tête du tableau à sa place définitive.
- Tri à bulle - OUI : séquence finale triée puisque la "bulle" qui remonte permet de propager l'élément à sa bonne place dans la fin du tableau
- Tri fusion -NON : l'élément minimum, s'il figure dans la moitié droite du tableau initial, ne sera inséré à sa place que par la fusion finale.
- Tri par insertion -NON : la séquence initiale peut-être à tout moment modifiée par l'insertion d'un élément inférieur aux éléments déjà visités.
Exercice 1 (6 points)
On considère la fonction suivante :
fonction Chebyshev (val n,x: entiers):entier;
debut
si n=0 alors
retourner(1);
sinon
si n=1 alors
retourner(x);
sinon
retourner(2*x*Chebyshev(n-1,x)-Chebyshev(n-2,x));
finsi
finsi
fin
- Quel est le résultat de l'appel Chebyshev(5,2)?
Donner l'empilement des contextes de chaque appel effectué.
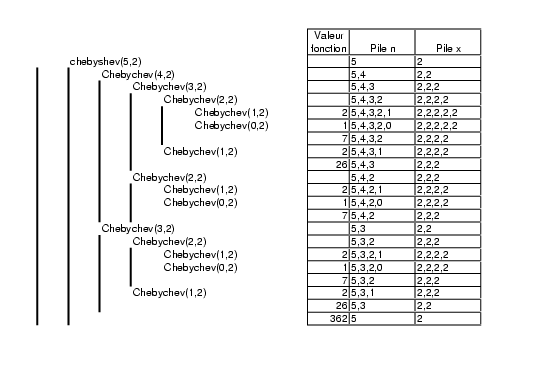
Chebyshev(3,y) retourne la valeur 4*y^3-3*y
Si on choisit comme opération pertinente le nombre d'appels, alors ce programme est identique en terme de nombre d'appels à celui calculant la suite de Fibonacci de manière récursive:
- 2 valeurs particulières donnent fin à la récursivité,
- tout autre appel génère deux appels.
Exercice 2 (8 points)
- On appelle MINIMAX d'une matrice d'entiers la valeur
minimale des maxima de chaque ligne.
- Ecrire un algorithme qui donne la valeur MINIMAX d'une matrice d'entiers nXm ainsi que l'emplacement du MINIMAX dans cette matrice. On précisera la nature de l'algorithme (fonction ou procédure) ainsi que le type et les modes de passages des paramètres.
- la matrice M passée par référence pour ne pas provoquer de copie en mémoire
- les dimensions n et m de la matrice passées par valeur,
- les résultats sont passés par référence MM la valeur recherchée, L et C la position ligne colonne de MM.
- Evaluer la complexité de votre l'algorithme (on précisera
l'opération pertinente servant à évaluer cette complexité qui pourra
être, ici, la comparaison de deux éléments de la matrice).
Il y a deux boucles pour imbriquées et chacune comporte un test donc la complexité est nm.
- Peut-on améliorer la complexité de cet algorithme en
triant chaque ligne de la matrice ?
Si la matrice n'est pas triée, cela veut dire que l'on trierait chaque ligne. la complexité du tri (puisqu'on ne connait pas des bornes a priori des entiers) est mlog(m). Par suite la complexité de la procédure deviendrait nmlog(m) ce qui est moins bon en complexité.
L'algorithme est une procédure. Les paramètres sont :
procédure MinMax(ref M:tableau[1..n,1..m] d'entiers;
val n,m:entiers;
ref MM,L,C: entiers);
var iL,iC,CMax:entiers;
début
L:=1;C:=1;
pour iL allant de 1 à n faire
CMax:=1;
pour iC allant de 1 à m faire
si M[iL,iC]>M[iL,CMax] alors
CMax:=iC
finsi
finpour;
si M[L,C]>M[iL,CMax] alors
L:=iL;C:=CMax;
finsi
finpour;
MM:=M[L,C];
finprocedure