Question de cours (4 points)
- Expliquer à quoi servent les tables de hachage.
Les tables de hachages permettent un accès à des éléments rapides sans les trier. Pour tout élément e on associe une valeur h(e) entière dans un intervalle [0..M]. l'application de hachage h n'est pas bijective.Voir des explications plus complètes
- Pourquoi le choix de la fonction de hachage est-il important ?
Quelles sont les erreurs à éviter ?
Le choix de la fonction de hachage dépend des données à traiter. Elle doit minimiser les collisions. Comme elle utilise en général la fonction modulo, il faut impérativement que M+1 soit un grand entier premier.
- Donner deux implémentations possibles des tables de
hachage. Dans les deux cas, préciser le résultat de l'insertion de
la suite (11, 23, 7, 15, 18, 4) avec comme fonction de hachage h(x)
= x modulo 7.
- Chaînage externe
Figure
- Stockage interne et traitement des collisions par
placement dans la première case libre (modulo 7) à partir de la case
calculée.
T[0]=7;T[1]=15;T[2]=23;T[3]=NULL;T[4]=11;T[5]=18;T[6]=4
- Chaînage externe
Exercice 1 (8 points)
On rappelle l'algorithme récursif de parcours en profondeur d'un arbre :
procedure Parcours(val x: sommet)
debut
(1)
si Existe_Fils(x) alors
(2)
y := Premier_Fils(x);
Parcours(y);
(2')
tant que Existe_Frere(y) faire
(3)
y := Frere(y);
Parcours(y);
(3')
fin tantque
sinon
(4)
fin si
(5)
fin
- Modifier Parcours pour calculer la plus petite profondeur d'une feuille, c'est à dire la plus courte distance de la racine à une feuille de l'arbre.
fonction Parcours(val x: sommet)
var minLocal:entier
debut
si Existe_Fils(x) alors
(2)
y := Premier_Fils(x);
minLocal:=1+Parcours(y);
(2')
tant que Existe_Frere(y) faire
(3)
y := Frere(y);
minLocal:=min(1+Parcours(y),minLocal);
(3')
fin tantque
sinon
(4) retourner(0)
fin si;
retourner(minLocal)
(5)
fin
Appel : k:=Parcours(x) avec type x:sommet; type k:entier;On considère que le type sommet est définit comme suit.
type sommet:entier;A tout moment le nombre de sommets d'un arbre peut être renvoyé par la procédure récursive donc qu'elle soit transformée en fonction.
fonction Parcours(val x: sommet;ref taille:tableau[1..N] d'entiers):entier;
debut
(1)taille[x]:=1;
si Existe_Fils(x) alors
(2)
y := Premier_Fils(x);
taille[x]:=taille[x]+Parcours(y);
(2')
tant que Existe_Frere(y) faire
(3)
y := Frere(y);
taille[x]:=taille[x]+Parcours(y);
(3')
fin tantque
fin si
(5) retourner(taille[x])
fin
Appel : k:=Parcours(x,taille) avec type x:entier; type taille:tableau[1..N]d'entiers;Exercice 2 (8 points)
On consid\`ere la procédure suivante :
procedure Mystere (ref A : Arbre);
var P1, P2 : Pile de sommet;
debut
Vider_Pile(P1);
Vider_Pile(P2);
Empiler(Racine(A),P1);
tant que non Pile_Vide?(P1) faire // boucle tant que principale
x := Valeur_Pile(P1);
afficher(x);
Depiler(P1);
si Existe_Fils?(x) alors
y := Premier_Fils(x);
Empiler(y, P2);
tant que Existe_Frere?(y) faire // 1ere boucle secondaire
y := Frere(y);
Empiler(y, P2);
fin tant_que;
tant que non Pile_Vide(P2) faire // 2eme boucle secondaire
Empiler(Valeur_Pile(P2), P1);
Depiler(P2);
fin tant_que;
fin si;
fin tant_que;
fin;
- Dessiner l'arbre de racine 1 ayant pour tableaux Premier_Fils et Frere
les valeurs suivantes :
Sommets 1 2 3 4 5 6 7 Premier_Fils 2 4 0 0 7 0 0 Frere 0 3 0 5 6 0 0
Figure
Le résultat de la procédure est l'affichage de 1 2 4 5 7 6 3.
- Etat de la pile P1 (le fond de pile est écrit en premier dans ce qui suit)
étape 1 : 1 étape 2 : 3,2 étape 3 : 3,6,5,4 étape 4 : 3,6,5 étape 5 : 3,6,7 étape 8 : 3,6 étape 9 : 3 étape 10 : sortie de boucle, la pile P1 est vide
- Etat Pile P2
Soit x le sommet de la boucle principale. Avant la première boucle secondaire la pile P2 contient le premier fils de x Avant la seconde boucle secondaire la pile P2 contient la liste des fils de x avec le premier fils en fond de pile.
Le résultat de la procédure est l'affichage de mot préfixe correspondant à l'arbre A. La pile P2 sert à mettre dans la pile P1 les fils de x dans le bon ordre pour le parcours préfixe.
Soit n le sommet de l'arbre. On considére les accès aux primitives de piles La complexité de mystère est la complexité de la boucle extérieure soit O(n). En effet, pour chaque sommet x visité par la boucle externe, la première boucle interne e empile les fils de x puis la seconde dépile les fils de x. Par suite, la complexité de chacune est en O(fils(x)). On a donc
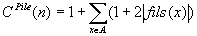
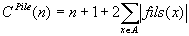
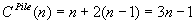
La complexité de mystère est donc en O(n).