Arbres
- Arbre et arborescence
- Arbres binaires
- Parcours d'un arbre binaire
- Implémentation d'un arbre binaire
- Retour sur les arborescences
- Parcours d'un arbre planaire
- Implémentation d'une arbre planaire
- Arbre et arborescence
Définition 4.1. Un arbre est un graphe connexe sans cycle.
Un sous arbre est un sous graphe d'un arbre.Propriété 4.2. Si un arbre a n sommets alors il a n-1 arêtes.
Idée de la démonstration
La taille d'un arbre est le nombre de sommets de l'arbre.
Ceci s'appuie sur les deux propriétés suivantes des graphes connexes.- Tout graphe connexe ayant n sommets a au moins n-1 arêtes.
- Tout graphe connexe ayant n sommet et au moins un cycle a au minimum n arêtes.
Propriété 4.3. Entre deux sommets quelconques d'un arbre, il existe une unique chaîne les reliant.
Idée de la démonstration
Pour deux sommets quelconques:- Il ne peut exister deux chaines différentes les reliant sinon il y aurait un cycle dans l'arbre.
- Il existe au moins une chaine puisque un arbre est un graphe connexe.
Définition 4.4. Une arborescence est définie à partir d'un arbre en choisissant un sommet appelé racine et en orientant les arêtes de sorte qu'il existe un chemin de la racine vers tous les autres sommets.
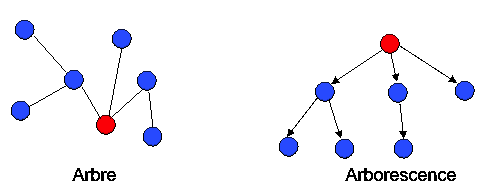
On notera qu'une arborescence est un exemple d'ensemble partiellement ordonné (relation d'ordre "fils de").
On appelle feuille de l'arbre un sommet qui n'a pas de successeur . Tout autre sommet est appelé sommet interne.
On appelle hauteur d'un sommet de l'arbre la longueur du chemin de la racine à ce sommet.
Définition 4.5. Un arbre planaire est défini en ordonnant les arêtes sortantes de chaque sommet.
On notera qu'un arbre planaire est un exemple d'ensemble totalement ordonné (relation "est fils ou est frère à droite").
Définition 4.6. Un arbre binaire est un arbre planaire dont chaque sommet a au plus deux fils.
Définition 4.7. Un arbre binaire complet est un arbre binaire dont chaque sommet interne a exactement deux fils.
Propriété 4.8. Tout sommet x d'un arbre binaire vérifie l'une des deux propriétés suivantes:
- x est une feuille,
- x a un sous arbre binaire dit gauche de racine G(x) et un sous arbre binaire droit de racine D(x).
Définition 4.9. Un arbre binaire parfait est un arbre binaire complet dans lequel toutes les feuilles sont à la même hauteur dans l'arbre.
Théorème 4.10Un arbre binaire de taille n a une hauteur est moyenne log2(n).
Théorème 4.11 Il existe une bijection qui transforme un arbre planaire ayant n sommet en un arbre binaire complet ayant 2n+1 sommets.
- Arbres binaires
Du fait de ce théorème, on ne considère dans un premier temps que le type arbre
binaire que l'on nommera arbreBinaire. Chaque sommet permet d'accéder
à deux sommets : le fils gauche et le fils droit.
Ce type sera nommé sommet. Chaque sommet
permet également d'accéder à l'objet qu'il stocke.
Un arbre binaire peut être vu comme un curseur indiquant le sommet
racine. De la même manière un sommet est un curseur.
On a donc
arbreBinaire=curseur; sommet=curseur;
Le type sommet présente les primitives suivantes :
- accès
fonction getValeur(val S:sommet):objet; /* vaut NULL si le sommet n'existe pas /* fonction filsGauche(val S:sommet):sommet; /* vaut NIL si S n'a pas de fils gauche */ fonction filsDroit(val S:sommet):sommet; /* vaut NIL si S n'a pas de fils droit */ fonction pere(val S:sommet):sommet; /* vaut NIL si S est la racine de l'arbre */
- modification
fonction setValeur(ref S:sommet;val x:objet):vide; /* affecte au sommet S la valeur x */ fonction ajouterFilsGauche(ref S:sommet,val x:objet):vide; /* filsGauche(S)==NIL doit être vérifié */ fonction ajouterFilsDroit(ref S:sommet,x:objet):vide; /* filsDroit(S)==NIL doit être vérifié */ fonction supprimerFilsGauche(ref S:sommet):vide; /* filsGauche(S) est une feuille */ fonction supprimerFilsDroit(ref S:sommet):vide; /* filsDroit(S) est une feuille */ fonction detruireSommet(ref S:sommet):vide; /* S est une feuille */
Il faut par ailleurs pouvoir créer la racine d'un arbre on a donc de plus la primitivefonction créerArbreBinaire(val Racine:objet):sommet;
et bien entendu détruire un arbrefonction detruireArbreBinaire(ref A:arbreBinaire d'objet):vide;
Détection de feuille
fonction estFeuille(val S:sommet):booléen; début retourner(filsGauche(S)==NIL et filsDroit(S)==NIL) finConstruction d'un arbre binaire à partir d'un tableau d'entiers
On choisit de remplir l'arbre de haut en bas et de gauche à droite (parcours hiérarchique).fonction remplirTableauArbre(ref T:tableau[1..N] d'entier): arbreBinaire d'entier; var A:arbreBinaire d'entier; var F: file de sommet; var s:sommet; var i:entier; début créerFile(F); A=créerArbreBinaire(T[1]); enfiler(F,A); tmp=2; tantque 2*tmp-1<=N faire pour i=tmp à 2*tmp-1 par pas de 2 faire s=valeur(F); defiler(F); ajouterFilsGauche(s,T[i]); enfiler(filsGauche(s)); ajouterFilsDroit(s,T[i+1]); enfiler(filsDroit(s)); finpour; tmp=tmp*2; fintantque pour i=tmp à N par pas de 2 faire s=valeur(F); defiler(F); ajouterFilsGauche(s,T[i]); ajouterFilsDroit(s,T[i+1]); finpour; si N mod 2 !=0 alors ajouterFilsGauche(valeur(F),T[N]) finsi detruireFile(F); retourner(A); fin
- accès
- Parcours d'un arbre binaire
Le parcours d'un arbre binaire consiste à donner une liste de sommets
dans l'arbre.
Le prototype d'algorithme ci-dessous permet d'effectuer
les parcours suivant les algorithmes associés aux traitements à
partir d'un sommet de l'arbre.
fonction parcoursArbreBinaire(val A:arbreBinaire d'objet):vide; // Déclarations locales début // traitement1; si estFeuille(A)alors // traitement2 sinon // traitement3; si filsGauche(A)!=NIL alors // traitement4; parcoursArbreBinaire(filsGauche(A)); // traitement5; finsi // traitement6; si filsDroit(A)!=NIL alors // traitement7 parcoursArbreBinaire(filsDroit(A)); // traitement8; finsi // traitement9; finsi // traitement1O; finComplexité: si le traitementi a pour complexité ci(n), soit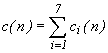 .
.
On distingue quatre parcours qui conditionnent les algorithmes sur les arbres binaires. Le parcours hiérarchique (voir paragraphe précédent) ainsi que les suivants :- Parcours préfixe On liste la racine, les sommets du sous arbre gauche, puis les sommets du sous arbre droit.
- Parcours infixe On liste les sommets du sous arbre gauche, puis la racine puis les sommets du sous arbre droit.
- Parcours suffixe On liste les sommets du sous arbre gauche, puis les sommets du sous arbre droit puis la racine.
Exemple
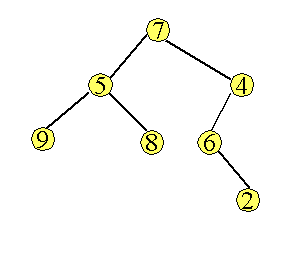
- Parcours préfixe :7 5 9 8 4 6 2
- Parcours infixe : 9 5 8 7 6 2 4
- Parcours suffixe : 9 8 5 2 6 4 7
Affichage des valeurs des sommets pour un parcours donné
Soit un arbre étiquetté par des entiers. On considère que l'on dispose de la fonction suivante qui affiche un entier n sur le terminal
fonction afficher(val n:entier):vide;
- Affichage dans le parcours préfixe
pas de déclarations locales. traitement 2, 3 : afficher(valeur(A));
- Affichage dans le parcours infixe
pas de déclarations locales. traitement 2, 6: afficher(valeur(A));
- Parcours suffixe
pas de déclarations locales. traitement 2, 9 : afficher(valeur(A));
Lister les étiquettes d'un arbre dans un tableau
fonction arbre2Tableau(val A:arbreBinaire d'entier;ref T:tableau[1..N] d'entier;ref i:entier):vide; début i=i+1; T[i]=valeur(A); si !estFeuille(A)alors si filsGauche(A)!=NIL alors arbre2Tableau(filsGauche(A),T,i); finsi si filsDroit(A)!=NIL alors arbre2Tableau(filsDroit(A),T,i); finsi finsi finHauteur d'un arbre binaire
fonction hauteurArbreBinaire(val s:sommet):entier début si estFeuille(s)alors retourner(0) sinon var tmp1,tmp2:entier; tmp1=0; tmp2=0; si filsGauche(s)!=NIL alors tmp1= hauteurArbreBinaire(filsGauche(s)); finsi si filsDroit(s)!=NIL alors tmp2=hauteurArbreBinaire(filsDroit(s)); finsi retourner(1+max(tmp1,tmp2)); finsi finAutre versionfonction hauteurArbreBinaireSimp(val s:sommet):entier début si s==NILalors retourner(-1) sinon retourner(1+max(hauteurArbreBinaireSimp(filsGauche(s)),hauteurArbreBinaireSimp(filsDroit(s)))); finsi finRemarque : La fonction hauteurArbreSimp (même si elle est plus courte) a une complexité plus grande que la fonction hauteurArbreBinaire notamment en nombre d'appel récursif. Elle est moins performante.Taille d'un sous-arbre d'un arbre binaire complet.
fonction tailleArbreBinaire(val A: arbreBinaire):entier; var tmp:entier; début si estFeuille(A) alors retourner(1) sinon retourner(1+tailleArbreBinaire(filsGauche(A)) +tailleArbreBinaire(filsDroit(A)) finsi fin
- Implémentation du type arbreBinaire
L'implémentation se fait par allocation dynamique.
On définit
cellule=structure info:objet; gauche:sommet; droit:sommet; pere:sommet; finstructure sommet=^cellule;On a alors- accès
fonction getValeur(val S:sommet):objet; début retourner(S^.info); fin fonction filsGauche(val S:sommet):sommet; début retourner(S^.gauche) fin fonction filsDroit(val S:sommet):sommet; début retourner(S^.droit) fin fonction pere(val S:sommet):objet; début retourner(S^.pere); fin - modification
fonction créerArbreBinaire(val racine:objet):sommet; var tmp:sommet; début new(tmp); tmp^.info=racine; tmp^.gauche=NIL; tmp^.droit=NIL; tmp^.pere=NIL; retourner(tmp) fin fonction ajouterFilsGauche(ref S:sommet,val x:objet):vide; var tmp:sommet; début new(tmp); tmp^.info=x; tmp^.gauche=NIL; tmp^.droit=NIL; tmp^.pere=S; S^.gauche=tmp; fin fonction ajouterFilsDroit(ref S:sommet,val x:objet):vide; var tmp:sommet; début new(tmp); tmp^.info=x; tmp^.gauche=NIL; tmp^.droit=NIL; tmp^.pere=S; S^.droit=tmp; fin fonction supprimerFilsGauche(ref S:sommet):vide; début delete(S^.gauche); S^.gauche=NIL; fin fonction supprimerFilsDroit(ref S:sommet):vide; début delete(S^.droit); S^.droit=NIL; fin fonction detruireArbreBinaire(ref A:arbreBinaire d'objet):vide; /* parcours suffixe */ début si estFeuille(A)alors delete(A) sinon si filsGauche(A)!=NIL alors detruiresArbreBinaire(filsGauche(A)); finsi si filsDroit(A)!=NIL alors detruireArbreBinaire(filsDroit(A)); finsi delete(A); finsi fin
- accès
- Retour sur les arbres planaires
On peut définir un type abstrait sommetArbrePlanaire par les primitives
suivantes:
- accès
fonction getValeur(val S:sommetArbrePlanaire):objet; fonction premierFils(val S:sommetArbrePlanaire):sommetArbrePlanaire; fonction frere(val S:sommetArbrePlanaire):sommetArbrePlanaire; fonction pere(val S:sommetArbrePlanaire):sommetArbrePlanaire;
- modification
fonction créerArbrePlanaire(val racine:objet):sommetArbrePlanaire; fonction ajouterFils(ref S:sommetArbrePlanaire,val x:objet):vide; /* ajoute un fils comme cadet */ fonction supprimerSommet(ref S:sommetArbrePlanaire):vide; /* le sommet doit être une feuille */ fonction detruireArbrePlanaire(ref S:sommetArbrePlanaire):vide;
- accès
- Parcours d'un arbre planaire
Le parcours d'un arbre planaire consiste à donner une liste de tous
les sommets.
Le prototype d'algorithme ci-dessous permet d'effectuer
les parcours suivant les algorithmes associés aux traitements à
partir d'un sommet de l'arbre planaire.
fonction parcoursArbrePlanaire(val A:sommetArbrePlanaire):vide; // Déclarations locales var f: sommetArbrePlanaire; début // traitement1; f= premierFils(A); tant que f!=NIL faire // traitement2; parcoursArbrePlanaire(f); // traitement3; f=frere(f); // traitement4 fintantque // traitement5 finOn distingue trois parcours qui conditionnent les algorithmes sur les arbres planaires. Le parcours hiérarchique qui s'effectue grâce à une file ainsi que- Parcours préfixe On liste la racine, les sommets de chaque sous arbre dans l'ordre où les sous arbres apparaisssent.
- Parcours suffixe On liste les sommets des sous arbres en ordre inverse puis la racine.
Exemple
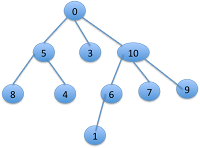
- Parcours préfixe : 0 5 8 4 3 10 6 1 7 9
- Parcours suffixe : 8 4 5 3 1 6 7 9 10 0
- Parcours hiérarchique : 0 5 3 10 8 4 6 7 9 1
- Implémentation du type arbrePlanaire
Implémentation dans le type arbreBinaire
L'implémentation dans le type arbreBinaire découle du théorème 4.11. On a alors
arbrePlanaire=arbreBinaire. Pour un noeud donné :- la primitive filsGauche donne accès au premier fils du noeud.
- la primitive filsDroit donne accès au frère du noeud.
- la primitive pere donne accès soit au père du noeud soit à son frère précédent. Il faut donc redéfinir la primitive pere pour les arbres planaires.
fonction pereArbrePlanaire(val S:sommetArbrePlanaire):sommetArbrePlanaire; var T: sommetArbrePlanaire; début T=filsGauche(pere(S)); tant que T!=S faire S=pere(S) T=filsGauche(pere(S)); fintantque retourner(pere(S)) finEn utilisant le théorème 4.10, cette dernière primitive à une complexité moyenne O(log2n).Implémentation par allocation dynamique
Cette implémentation permet de diminuer le temps d'accès au père.celluleAP=structure info:objet; premierFils:sommet; frère:sommet; père:sommet; finstructureDans cette implémentation, on initialise parfois le champ frere du dernier frère à l'adresse du frère ainé. On peut vérifier aisément que les primitives sont toutes réalisables en O(1). L'espace mémoire est le même que celui occupé par une implémentation dans le type arbreBinaire.- accès
fonction getValeur(val s:sommetArbrePlanaire):objet; début retourner(s^.info) fin fonction premierFils(val s:sommetArbrePlanaire):sommetArbrePlanaire; début retourner(s^.premierFils) fin fonction frere(val S:sommetArbrePlanaire):sommetArbrePlanaire; début retourner(s^.premierFils) fin fonction pere(val s:sommetArbrePlanaire):sommetArbrePlanaire; début retourner(s^.pere) fin - modification
fonction créerArbrePlanaire(val racine:objet):sommetArbrePlanaire; var tmp:^celluleAP; début new(tmp); tmp^.info=racine; tmp^.premierFils=NIL; tmp^.frere=NIL; tmp^.pere=NIL; retourner(tmp) fin fonction ajouterFils(ref s:sommetArbrePlanaire,val x:objet):vide; /* ajoute un fils comme cadet */ /* cette fonction n'est pas en O(1) */ var tmp:^celluleAP; début new(tmp); tmp^.info=x; tmp^.frere=NIL; tmp^.pere=s; si s^.premierFils==NIL alors s^.premierFils=tmp; sinon r=premierFils(s); tantque frere(r)!=NIL faire r=frere(r) fintantque r^.frere=tmp fin fonction supprimerSommet(ref s:sommetArbrePlanaire):vide; /* le sommet doit être une feuille */ var p,r,tmp:^celluleAP; début r=premierFils(pere(s)); si r==s alors p=pere(s); p^.premierFils=s^.frere; sinon tantque frere(r)!=s faire r=frere(r); fintantque r^.frere=s^.frere; finsi delete(s) fin fonction detruireArbrePlanaire(ref s:sommetArbrePlanaire):vide; var tmp,f: sommetArbrePlanaire; début f= premierFils(s); tant que f!=NIL faire parcoursArbrePlanaire(f); f=frere(f); fintantque supprimerSommet(s) fin