Licence Semestre 2 Initiation à l'algorithmique
Dernière mise à jour effectuée le 2 Juillet 2007
Retour sur les fonctions, Récursivité
- Visibilité
Comme vu au chapitre Codage et structures de contrôle,on peut déclarer dans une fonction des variables et des fonctions locales.
fonction NomDeFonction (ListeParamètres):TypeRésultat; //déclarations des variables ou fonctions locales début // partie instruction qui contient l'appel à retourne fin finFonctionLa multi-imbrication possible des fonctions entraîne l’existence de problèmes de visibilité : entre les variables et entre les fonctions.Visibilité d'une variable
- Règle 1 : Une variable V (locale ou non) est visible depuis sa déclaration jusqu’au marqueur finFonction de la fonction F où elle a été déclarée.
- Règle 2 : Si une fonction G est locale à F et déclare une variable V déjà déclarée dans F alors la variable originelle est momentanément cachée.
Exemple
Soit la fonction P suivante
fonction P (....):....; var x,y,z : entier ; fonction R():vide; var z,u,v : entier ; début z=0; u=6; ... fin ; finFonction fonction Q(ref x:entier ):....; var u,y : entier ; début y=4; x=x+y; u=7 fin ; finFonction début x=1; y=2; z=3; R() ... Q(z); fin finFonction- La fonction P déclare 3 variables locales x, y, z et deux fonctions locales Q et R,
- La fonction Q déclare 2 variables locales u, y et un paramètre x,
- La fonction R déclare 3 variables locales z, u et v.
Visibilité d'une fonction
Une fonction est visible depuis la fin de son entête jusqu’au finFonction de la fonction où elle a été déclarée. Cependant comme pour les variables, elle peut momentanément être cachée par une autre fonction ayant la même entête (surcharge).Exemple
La fonction P suivante est anotée pour préciser la visibilité des fonctions Q,R,T.
fonction P(....):....; ..... fonction Q(....):.....; ..... fonction R(...):.....; .... début ....// on peut utiliser P,Q,R fin finFonction ; début ....// on peut utiliser P,Q,R finFonction fonction T(...):...; début ....// on peut utiliser P,Q,T mais pas R finFonction ; début ... //// on peut utiliser P,Q,T mais pas R fin finFonction
- Récursivité
La récursivité consiste à remplacer une boucle par un appel à la fonction elle-même. Considérons la suite factorielle, elle est définie par :
0!=1
La fonction peut s'écrire simplement
n!=n(n-1)!
On a le déroulement ici. On peut décrire sur le papier les changements et les appels sous la forme suivante :fonction factorielle(val n:entier):entier; début si (n==0) retourne(1) sinon retourne(factorielle(n-1)*n) finsi fin finfonction;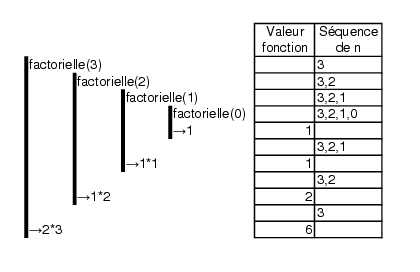
Plusieurs appels à la fonction peuvent être exécutés dans son corps. Soit la suite dite de Fibonacci définie par :u0=1
la fonction s'écrit tout aussi simplement
u1=1
un=un-1+un-2 pour n > 2
On a le déroulement ici On peut décrire sur le papier les changements et les appels sous la forme suivante :fonction fibo(val n:entier):entier; début si (n==0) ou (n==1) alors retourne(1) sinon retourne(fibo(n-1)+fibo(n-2)) finsi fin finfonction;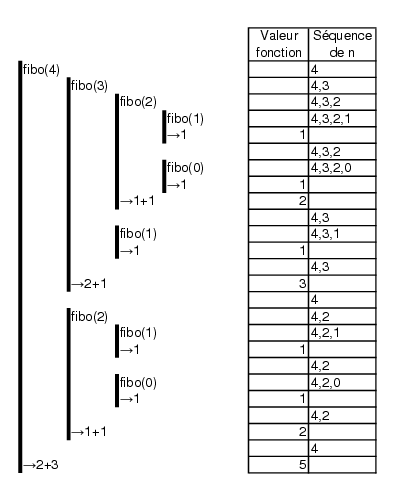
- Complexité
Examinons la suite définie par
u1=1
Une fonction permettant le calcul de son nième terme est :
un=un-1+n pour n > 1
L'exemple ci-dessus devient en algorithme récursif :fonction suite(val n:entier):entier; var i,s:entier; début s=0; pour i allant de 1 à n faire s=s+i; finpour; retourner(s) fin finfonction;
La complexité en nombre d'opération de suite et suiteR est en O(n). On aurait donc tendance à préférer suiteR pour sa lisibilité. Cependant si on examine la complexité en mémoire, suite est en O(1) alors que suiteR est en O(n). La programmation non récursive est donc plus efficace.fonction suiteR(val n:entier):entier; début si n==1 alors retourne(1) sinon retourne(suiteR(n-1)+n) finsi fin finfonction;
L'utilisation de la récursivité ne doit pas se faire au détriment de l'efficacité.
- Exemples
Chaque fois que l'on désire programmer une fonction récursive, on doit répondre aux questions suivantes :
- Comment le problème au rang n se déduit il de la solution à un (des) rang(s) inférieurs ?
- Quelle est la condition d'arrêt de la récursivité ?
Recherche d'un élément dans un tableau d'entier
fonction cherche(ref T:tableau[min_indice..max_indice] d'élément; val e: élément):entier; début si T[min_indice]==e alors retourner(min_indice) sinon si min_indice == max_indice alors retourner(NULL) sinon retourner(cherche(T[min_indice+1..max_indice],e)) finsi finsi fin finfonctionMinimum dans un tableau d'entier
fonction minimumTableau(ref T:tableau[1..N] d'entiers; val Imin:entier):entier; var sauv:entier; début si Imin==N alors retourner(T[N]) sinon sauv= minimumTableau(T,Imin+1]; si T[Imin]<sauv alors retourner(T[Imin]) sinon retourner(sauv) finsi finsi fin finfonction