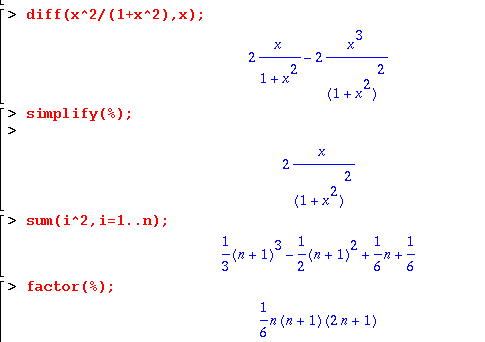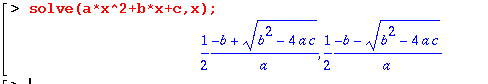Maple - Généralités
Qu'est ce que Maple
-
Maple est un langage de programmation interactif qui fonctionne sur tous
les systèmes d'exploitation.
-
Maple permet de traiter aisément beaucoup de calculs mathématiques
de manière numérique mais aussi et surtout formelle.
-
Il a été conçu vers 1980 par des chercheurs de l'Université
de Waterloo (Canada).
Les briques de bases
-
les constantes
-
nombres entiers,
-
rationnels,
-
flottants ("réels"),
-
prédéfinies : Pi, false,
true,
infinity,...
-
les chaînes de caractères
-
les noms : Maple fait la différence entre les majuscules et les
minuscules
-
les opérateurs : + * - / ^ < > <= >=
. and or not
-
les intervalles : expression..expression
Les listes et les ensembles
Un ensemble est non ordonné : {suite
d'expressions}.
Les opérations sur les ensembles sont : member
union minus intersect.
Une liste est ordonnée : [suite
d'expressions] Toute expression maple
est une liste. Par exemple 3+x+y est considéré par Maple
comme l'opérateur + appliqué à la liste [3,x,y]. Quelques
fonctions d'accès à une liste sont:
-
nops(expression) : nombre d'opérandes
-
op(k,expression) où k
est un entier : kième opérande de l'expression
-
op(k..m, expression) où
k et m sont des entiers : suites des opérandes de k à m
Il existe des raccourcis pour ces primitives. Soit L une liste (ou un ensemble) alors :
- l[k] représente le kième élément,
- l[k..m] représente la liste (ou l'ensemble) des éléments de k à m.
Evaluation.
Toute expression Maple retourne une valeur. Les fonctions eval
permettent de forcer Maple à évaluer une expression. Quelques
exemples :
-
evalf(3/4) donne le résultat 0.75
-
eval(x^2+1,x=3) donne 10
-
evalb(4=5) donne false
Quelques fonctions.
Maple possède toutes les fonctions classiques sin, cos, sqrt, exp,
log, ... Sa spécificité réside surtout dans sa bibliothèque
de fonctions qui peuvent être éxécutées sur
des expressions non numériques (formelles). Voici quelques exemples.
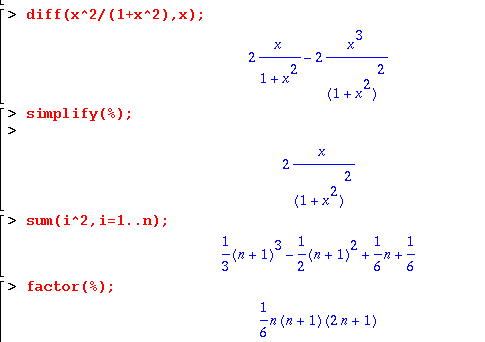
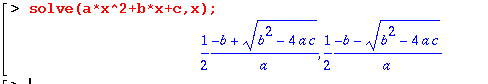
Pour utiliser certaines fonctions, il faut le préciser à
maple pour qu'il charge les bibliothèques correspondantes.
C'est le cas par exemple pour les bibliothèques statistiques.
L'instruction à utiliser est with.
Par exemple, pour les statistiques, il faut au préalable exécuter
with(stats).
On peut aussi tracer des fonctions en 2D et 3D. On peut faire tourner
un graphique 3D afin de l'explorer.