 Méthodes statistiques pour l'informatique
18 octobre 2004
Méthodes statistiques pour l'informatique
18 octobre 2004
 Méthodes statistiques pour l'informatique
18 octobre 2004
Méthodes statistiques pour l'informatique
18 octobre 2004
Exercice 1
On rappelle qu'une v.a. ![]() suit la loi binomiale de paramètres
suit la loi binomiale de paramètres ![]() si
si ![]() prends ses valeurs dans
prends ses valeurs dans ![]() avec la probabilité
avec la probabilité
![]() .
.
Quelle est la série génératrice d'une v.a. ![]() suivant la loi binomiale de paramètres
suivant la loi binomiale de paramètres ![]() ? En déduire l'espérance et la variance de
? En déduire l'espérance et la variance de ![]() .
.
Exercice 2
On rappelle qu'une v.a. ![]() suit une loi géométrique de paramètre
suit une loi géométrique de paramètre ![]() si
si ![]() prends ses valeurs dans
prends ses valeurs dans ![]() avec la probabilité
avec la probabilité
![]() .
.
Quelle est la série génératrice d'une v.a. ![]() suivant une loi géométrique de paramètre
suivant une loi géométrique de paramètre ![]() ? En déduire l'espérance et la variance de
? En déduire l'espérance et la variance de ![]() .
.
Exercice 3
On rappelle qu'une v.a. ![]() suit une loi de poisson de paramètre
suit une loi de poisson de paramètre ![]() si
si ![]() prends ses valeurs dans
prends ses valeurs dans ![]() avec la probabilité
avec la probabilité
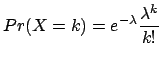 .
.
Quelle est la série génératrice d'une v.a. ![]() suivant la loi de poisson de paramètre
suivant la loi de poisson de paramètre ![]() ? En déduire l'espérance et la variance de
? En déduire l'espérance et la variance de ![]() .
.
Dans les 5 exercices ci-dessous, définir l'espace des évènements, la variable aléatoire en fonction de l'objectif poursuivi. Puis donner, si cela est possible, la loi de distribution à choisir dans ``binomiale'', ``Géométrique'', ``Poisson'' et dans ce cas préciser si possible l'espérance et la variance.
Exercice 4
Un virus informatique à son initialisation occupe ![]() . A chaque itération, il occupe
. A chaque itération, il occupe ![]() fois plus de mémoire, il s'arete avec la probabilité
fois plus de mémoire, il s'arete avec la probabilité ![]() en il libèrant la mémoire occupée. Dans quelle mesure ce virus risque-t-il de saturer la mémoire ?
en il libèrant la mémoire occupée. Dans quelle mesure ce virus risque-t-il de saturer la mémoire ?
Exercice 5
On doit prédimentionner un tableau, qui est une ressource pour un ensemble de processus : un processus qui s'exécute a besoin d'une entrée dans le tableau. Si aucune entrée n'est disponible alors il est mis en attente dans une file. On sait qu'en moyenne ![]() processus s'exécutent en même temps. Comment dimensionner le tableau pour qu'il n'y ait pas plus de 10% de processus en attente.
processus s'exécutent en même temps. Comment dimensionner le tableau pour qu'il n'y ait pas plus de 10% de processus en attente.
Exercice 6
Sur une séquence ![]() de
de ![]() bits, on ajoute un
bits, on ajoute un
![]() bit
bit ![]() défini par :
défini par :
Exercice 7
Un algorithme reçoit en entrée une liste d'entiers positifs. Sa complexité est une fonction du nombre d'entiers pairs ![]() ,
, ![]() . Donner des indications sur le comportement de l'algorithme.
. Donner des indications sur le comportement de l'algorithme.
Exercice 8
Un utilisateur peut à tout moment exécuter p processus différents avec la même probabilité. L'un de ces processus concerne l'impression. Étudier ce processus d'impression pour N utilisateurs.
Exercice 9
Nous sommes deux enfants. L'un de nous est une fille, quelle est la probabilité pour que l'autre soit un garçon ?
Exercice 10
On presente à un joueur trois sacs, dont l'un contient un prix. Le joueur choisi un sac sans l'ouvrir. L'animateur ouvre un des deux sacs restant et celui ci-est vide. Le joueur a alors le choix : ouvrir le dernier sac ou ouvrir celui qu'il a choisi au départ. Quelle est la conduite que doit adopter le joueur pour maximiser ses chances de gain ?
Exercice 11
On jette 3 dés authentiques. Quelle est la probabilité pour l'un d'eux
montre l'as, sachant qu'il n'y a pas eu de faces semblables ?
Exercice 12
Un controle systématique est effectué sur un ensemble de processeurs dont 15%
présentent une panne ![]() non apparente. Ce
dépistage est débuté par un test qui donne 95% de résultats positifs
pour les processeurs défectueux, et 10% de résultats positifs pour les
processeurs non défectueux.
non apparente. Ce
dépistage est débuté par un test qui donne 95% de résultats positifs
pour les processeurs défectueux, et 10% de résultats positifs pour les
processeurs non défectueux.
Quelle est la probabilité conditionnelle qu'un processeur pris au
hasard présente la panne ![]() sachant que le test a donné un résultat
positif ?
sachant que le test a donné un résultat
positif ?
Exercice 13
Une usine fabrique des barettes mémoire à l'aide de trois machines
A, B et C. La machine A assure 20% de la production et 5% des
barettes fabriquées par A sont défectueuses. La machine B assure 30% de
la production et 4% des barettes fabriquées par B sont défectueuses.
La machine C assure 50% de la production et 1% des barettes
fabriquées par C sont défectueuses.
Exercice 14
(Approximation poissonnienne)
On admet la proposition suivante. Soit
![]() , une suite de
v.a. à valeurs dans
, une suite de
v.a. à valeurs dans
![]() . Soit
. Soit
![]() , la suite des
f.g. Si
, la suite des
f.g. Si ![]() tend vers
tend vers ![]() la f.g. de la v.a.
la f.g. de la v.a. ![]() , alors la v.a.
, alors la v.a.
![]() tend vers
tend vers ![]() , i.e., pour tout
, i.e., pour tout
![]() ,
, ![]() tend vers
tend vers
![]() .
.
En utilisant la proposition précédente, montrer que, si ![]() est une
v.a. binomiale de paramètres
est une
v.a. binomiale de paramètres ![]() et
et ![]() tels que
tels que
![]() , alors
, alors ![]() tend vers
une v.a. de Poisson de paramètre
tend vers
une v.a. de Poisson de paramètre ![]() .
.
Dans une entreprise, 900 utilisateurs demandent chaque jour
à l'équipe système de recharger les imprimantes en papier
avec une probabilité ![]() . On suppose que chaque utilisateur a un
comportement indépendant des autres utilisateurs. Quel est le nombre
minimum de ramette de papier
que l'équipe système doit avoir en stock le matin si elle veut être en
mesure de pouvoir satisfaire l'ensemble des demandes avec une
probabilité supérieure ou égale à 0.95 ?
. On suppose que chaque utilisateur a un
comportement indépendant des autres utilisateurs. Quel est le nombre
minimum de ramette de papier
que l'équipe système doit avoir en stock le matin si elle veut être en
mesure de pouvoir satisfaire l'ensemble des demandes avec une
probabilité supérieure ou égale à 0.95 ?