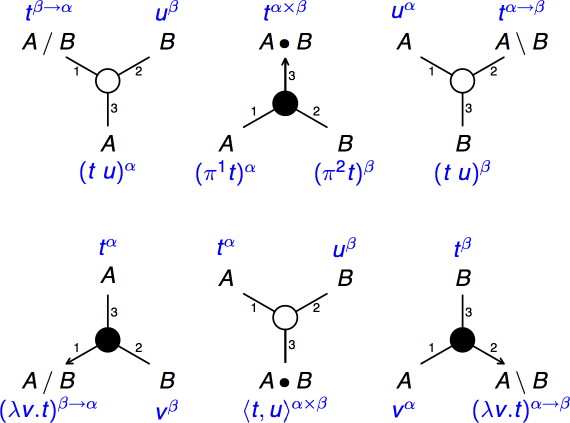
Figure 1. The graph connections with the corresponding typed lambda term semantics
This section gives a very brief introduction to the (extensional) typed lambda calculus. For more extensive and detailed introductions, see (Gamut 1991). Types τ are defined as follows: there are two basic types e (for entities) and t (for truth values) and two recursively defined types. When α and β are types, so are α → β and α × β. α → β is the set of functions from α to β whereas α × β is the Cartesian product of α and β.
For terms, we will often write tα to indicate term t is of type α, though, when the type can be deduced from the context we will often omit it. Given a set of variables vα (of each type α ∈ τ) and a set of constants cα (of each type α ∈ τ) we defined the set of terms as follows.
Clause 1 is the base case. It introduces both variables (1.a) and constants (1.b) into the system.
Clause 2 introduces the application (2.a) and abstraction operations (2.b) for the functional types.
Clause 3 introduces the pairing (3.a) and projection operations (3.b) for the Cartesian product types.
Clause 4 introduces the logical connectives of negation (4.a), conjunction, disjunction and implication (4.b), equality between terms of the same type (4.c) and the existential and universal quantifiers (4.d).
(We can also follow Church and treat the logical symbols ¬, ∧, ∀ etc. as constants. However, Grail follows the strategy indicated above in clause 4).
| (λv.t) u | =β | t[v:=u] |
| π1⟨t,u⟩ | =β | t |
| π2⟨t,u⟩ | =β | u |
Table 1. β-conversion rules.
An important theorem of the simply typed lambda calculus is that β conversion is confluent. In other words, whenever there are two ways to reduce a lambda term, both reductions will (eventually) reduce further to the same result term. As a consequence the normal form of a term is unique.
In addition, the calculation of a normal form is terminating. That is to say, any reduction sequence of beta steps is finite and ends with a normal form.
| type(s) | = | t |
| type(n) | = | e → t |
| type(np) | = | e |
| type(A/B) | = | type(B) → type(A) |
| type(B\A) | = | type(B) → type(A) |
| type(A•B) | = | type(A) × type(B) |
Table 2. Typing rules for basic and complex formulas.

Figure 1. The graph connections with the corresponding typed lambda term semantics
Find out how to represent typed lambda terms in your lexicon.