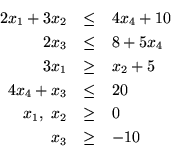Next: About this document ...
Recherche Opérationnelle
IUP-MIAGe 3
Mercredi 12 Novembre 1997
- 1.
- Pour les 3 parties de cette question vous pouvez prendre comme
exemple le programme linéaire suivant; mais vous ne devez pas limiter
vos réponses à cet exemple.
- (a)
- Comment peut-on mettre un programme linéaire en forme standard?
- (b)
- Comment utilise-t-on un autre programme linéaire pour trouver
une solution de base faisable du programme initial?
- (c)
- Quel est le dual d'un programme linéaire et quel est le rapport
entre les solutions du programme initial et celles du dual?
- 2.
- (a)
- Sous quelles conditions un système qui change aléatoirement
peut-il être décrit par une chaîne de Markov?
- (b)
- Donner une chaîne de Markov pour le système suivant:
Une compagnie de livraison de colis a deux véhicules. Chaque
véhicule est à Bordeaux ou à Paris chaque nuit. Si une demande
arrive le matin de livrer un colis d'une ville à l'autre et si
un véhicule est là pour effectuer la livraison, il le fait
et reste à l'autre ville la nuit suivante; sinon il reste dans
la même ville. Les probabilités de demandes de livraisons
dans les deux directions sont p1 (Bordeaux-Paris) et
p2 (Paris-Bordeaux).
- (c)
- La compagnie veut savoir s'il serait plus rentable, dans
les cas ou les deux véhicules seraient dans la même ville
une nuit, d'envoyer un véhicule vide à l'autre ville.
Si le profit d'une livraison est L et le coût d'un trajet
vide est V, décrire les calculs qu'on peut faire pour
décider cette question.



Next: About this document ...
Mike ROBSON
2000-11-27