| x5 + x6 | 10 | (1) | |
| x4-x5 | 10 | (2) | |
| x3-x5-x6 | 10 | (3) | |
| x2-x4+x5-x6 | 10 | (4) | |
| x1-x2+x4-2x5+x6 | 10 | (5) | |
| -x2+x4-x5+x6 | 0 | (6) | |
| -x1+x2-x4+2x5-x6 | 0 | (7) | |
| x1,x2,x3,x4,x5,x6 | 0 | (8) | |
| zmin | = | -6x1+5x2-5x4+13x5-3x6 | (9) |
- (a)
- Démontrez que
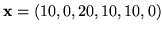 ,
,
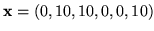 et
et
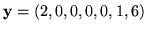 sont des solutions faisables de
base du programme et de son dual,
sont des solutions faisables de
base du programme et de son dual,
- (b)
- Quelles sont les valeurs des fonctions objectives pour ces trois solutions?
- (c)
- Que peut-on déduire de la réponse précédente (et pourquoi)?
- (d)
- Donner une solution faisable du programme initial qui n'est pas une solution de base et qui donne la valeur optimale de la fonction objective,
- (e)
- Expliquer pourquoi, dans la recherche de la valeur optimale d'un programme linéaire possédant une solution optimale, il suffit de considérer les solutions de base,
- (f)
- Combien de solutions de base possède le programme initial (y compris celles qui ne sont pas faisables)?
- (a)
- Expliquez, pour une chaîne de Markov avec une seule classe finale qui n'est pas périodique, comment vous pouvez trouver la limite de la probabilité d'être dans un état donné.
- (b)
- Pourquoi votre méthode ne donne-t-elle pas forcément le bon résultat dans le cas de plusieurs classes finales et dans le cas d'une classe finale périodique?
- (c)
- Supposez que dans une chaîne l'état i est périodique
avec période
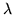 et que l'état initial est l'état 1.
Comment calcule-t-on la limite de la probabilité d'être dans
l'état i après un nombre de transitions qui est un multiple
de
et que l'état initial est l'état 1.
Comment calcule-t-on la limite de la probabilité d'être dans
l'état i après un nombre de transitions qui est un multiple
de 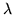 ?
?