- (a)
- en utilisant un parcours naïf des sommets du polytope
si le nombre d'itérations était m+n?
(m+n)n(m-n) - (b)
- en calculant tous les sommets une fois?
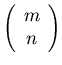
192, 1536, 12288 (parcours)
70, 601080390, 1832624140942590464
(Et même plus d'une fois)
Considérez un réseau de lignes sur la surface d'un demi globe où le point initial est le pôle sud et la fonction objective monte en allant vers le nord. On peut construire un chemin de Pi à Qi à Pi+1 où tous les P sont sur le plan qui coupe le globe en deux et tous les Q sont un peu à l'est. Il y a aussi des lignes Pi-Ri, Ri-Pi+1 Qi-Ri, et Qi-Si avec Ri sur le plan, entre Pi et Pi+1 et un peu au sud-ouest de Qi et Si est au nord de Qi et au sud-ouest de Pi+1. Donc le chemin Pi-Qi-Pi+1 est le chemin trouvé par l'algorithme. En ajoutant des lignes de sorte que toute section de la surface du demi globe entourée des lignes est un triangle, et définissant une contrainte dont l'équation est celle du plan qui contient les trois sommets de chaque triangle, on découvre le programme linéaire avec les propriétés souhaitées.
(Plus facile à démontrer quà décrire en mots!)
- (a)
- Démontrer qu'un polytope en dimension n et à 2n faces peut avoir (au moins) 2n sommets.
- (b)
- Et qu'il y a un chemin simple qui parcourt tous les sommets.
- (c)
- Est-il possible qu'un parcours qui choisit à chaque
itération un voisin aléatoire avec une valeur de la fonction objective
supérieure à celle du sommet actuel suive un tel chemin?
Oui.
Je vais construire récursivement, en dimension n un ensemble de 2n points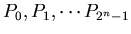 bornée par 2n hyperplans
et une fonction linéaire
bornée par 2n hyperplans
et une fonction linéaire
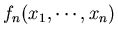 telle que
fn monte en parcourant le chemin
telle que
fn monte en parcourant le chemin
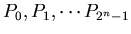 à partir de la valeur fn(P0)=0.
à partir de la valeur fn(P0)=0.
Pour n=1 c'est trivial.
Pour construire les points et la fonction en dimension n+1 de ceux de dimension n:- Les nouveaux points Pi avec i<2n sont construits par l'ajout d'une valeur xn+1=0 à l'ancien Pi
- Soit M la valeur maximum de fn sur les points
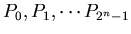 ,
à savoir
fn(P2n-1).
Le nouveaux point
P2n+1-1-i (i<2n) est construit
de l'ancien point Pi en ajoutant la nouvelle valeur
xn+1=2M+1-fn(Pi).
,
à savoir
fn(P2n-1).
Le nouveaux point
P2n+1-1-i (i<2n) est construit
de l'ancien point Pi en ajoutant la nouvelle valeur
xn+1=2M+1-fn(Pi).
Donc ces nouveaux points sont sur l'hyperplan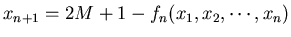 .
.
- La nouvelle fonction est
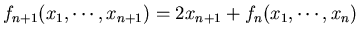 .
.
On trouve que fn+1 monte en parcourant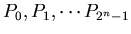 parce que xn+1=0 et donc fn+1 prend la même suite de
valeurs
que celles de fn sur les anciens Pi,
parce que xn+1=0 et donc fn+1 prend la même suite de
valeurs
que celles de fn sur les anciens Pi,
fn+1(P2n)=max+1>max=fn+1(P2n-1),
fn+1 monte en parcourant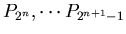 parce que la terme 2xn+1 monte deux fois plus vite que fn
baisse.
parce que la terme 2xn+1 monte deux fois plus vite que fn
baisse.
fn+1(P2n+1-i)-fn+1(P2n+1-i-1)= 2(xn+1[P2n+1-i]-xn+1[P2n+1-i-1]) +fn(Pi-1)-fn(Pi)= 2(2M+1-fn(Pi-1)-(2M+1-fn(Pi)))+fn(Pi-1)-fn(Pi)=fn(Pi)-fn(Pi-1)>0