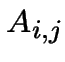 pour la transition de
pour la transition de
Coût d'une transition: 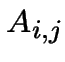 pour la transition de
pour la transition de ![]() à
à ![]() (ne dépend pas du temps ni de l'histoire)
(ne dépend pas du temps ni de l'histoire)
Coût moyen d'une transition: de l'état ![]() :
:
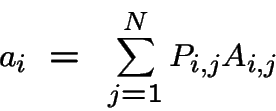
Tendance vers la moyenne:
Le coût moyen par transition tend vers ![]() où
où ![]() est le coût moyen d'une transition dans la distribution limite
est le coût moyen d'une transition dans la distribution limite ![]()
On peut facilement calculer ![]() :
:
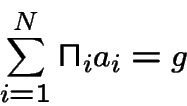
La possibilité de choix: supposons que dans l'état ![]() on peut choisir
entre plusieurs décisions et que pour la décision
on peut choisir
entre plusieurs décisions et que pour la décision ![]() , la probabilité
d'aller en état
, la probabilité
d'aller en état ![]() est
est 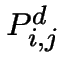 avec un coût
avec un coût 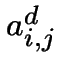
on peut calculer l'espérance du coût d'une transition:
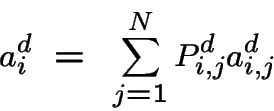
Le nombre de politiques possibles peut être trop grand pour
permettre de calculer le ![]() de chacune
de chacune
et peut-être ce n'est pas la politique possédant le plus petit ![]() qu'il convient de choisir...
qu'il convient de choisir...
Un compromis entre la politique gloutonne et minimiser ![]()
Actualisation: Un euro aujourd'hui est plus utile qu'un euro l'année prochaine;
Un coût d'un euro aujourd'hui est plus grave qu'un pareil coût l'année prochaine;
On veut calculer les coûts sur la supposition qu'un euro au temps ![]() vaut
vaut ![]() euros au temps
euros au temps 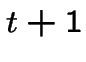 ;
; 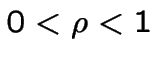 .
.
Rapport avec le taux d'intérêt: si le taux réel d'intérêt (payé ou reçu) est ![]() ,
on a
,
on a
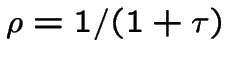 .
.
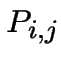 de transition de l'état
de transition de l'état
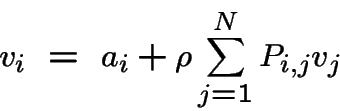
Système non singulier: on peut calculer les ![]() de ces équations
parce que
de ces équations
parce que
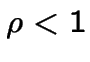 .
.
Le coût dans la distribution limite: Si le coût moyen d'une transition dans
la distribution limite (sans actualisation) est ![]() , le coût (total) si on commence dans cette
distribution est
, le coût (total) si on commence dans cette
distribution est
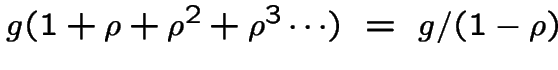 .
Donc
.
Donc
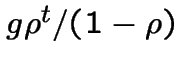 est une approximation au coût à partir de temps
est une approximation au coût à partir de temps ![]() (
(![]() grand et la chaîne régulière).
grand et la chaîne régulière).
On peut utiliser l'algorithme d'amélioration d'une
politique initiale: calculer le coût total (avec actualisation) ![]() à partir de
chaque état
à partir de
chaque état ![]() ; choisir à chaque état
; choisir à chaque état ![]() la décision
la décision ![]() qui minimise
qui minimise
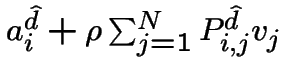 ;
répéter tant qu'il y a une réduction;
;
répéter tant qu'il y a une réduction;
(Ca équivaut à
minimiser le coût qu'on aurait si on choisissait une nouvelle
politique pour la première étape et gardait l'ancienne politique
après, ce qui explique pourquoi il y a amélioration)
D'abord avec les décisions ![]() on a:
on a:
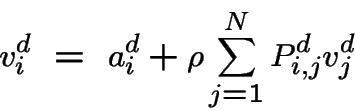
On choisit ![]() tel que
tel que
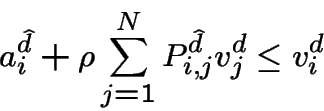
Les vrais nouveaux coûts sont donnés par:
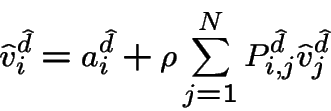
Donc:
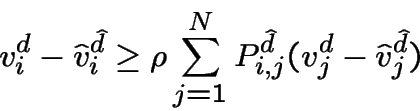
Considérons le ![]() qui donne le minimum de
qui donne le minimum de
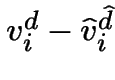 : on a
: on a
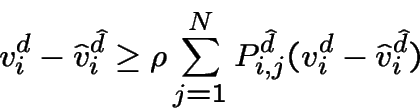
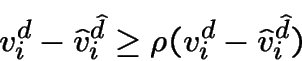
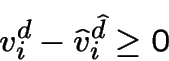
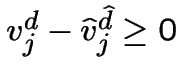 pour tout
pour tout
Finalement on ne peut pas avoir ![]() pour tout
pour tout ![]() ; et donc on a une amélioration pour
tout
; et donc on a une amélioration pour
tout ![]() ...
...
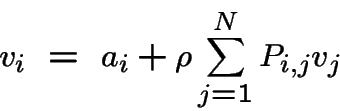
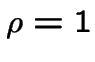 ; (soit aucune solution,
soit plusieurs)
; (soit aucune solution,
soit plusieurs)
On peut définir 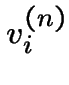 le coût moyen d'une
suite de
le coût moyen d'une
suite de ![]() transitions à partir de l'état
transitions à partir de l'état ![]() .
On trouve que
.
On trouve que
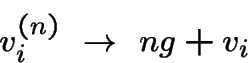
On a
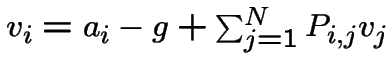
mais ces équations ne suffisent pas (ajout de la même
constante ![]() à chaque
à chaque ![]() donne une nouvelle solution)
Il faut ajouter
donne une nouvelle solution)
Il faut ajouter
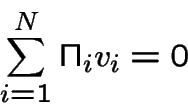
On essaie d'optimiser la politique en utilisant la même idée que dans le cas avec actualisation:
 et supposons les coûts actualisés au
début
de l'année)
et supposons les coûts actualisés au
début
de l'année)
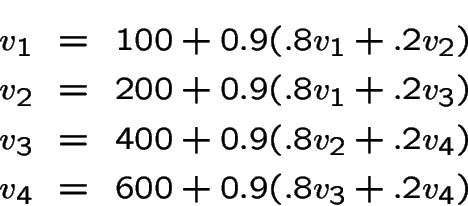
![$\color {red}{\bf v}=[1315,1489,1905,2405]$](img49.gif)
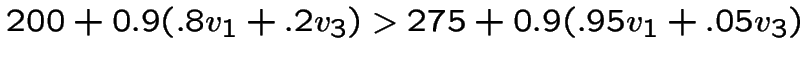 ):
):
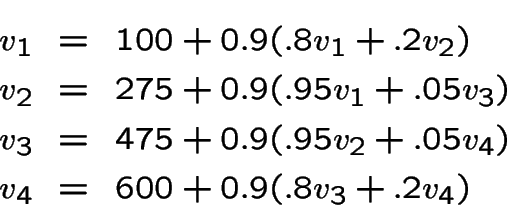
![$\color {red}{\bf v}=[1304,1472,1839,2347]$](img53.gif) Maintenant on voit qu'une meilleur politique à
Maintenant on voit qu'une meilleur politique à 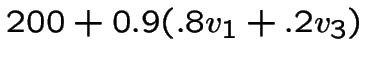
 )
)
Donc, une troisième politique:
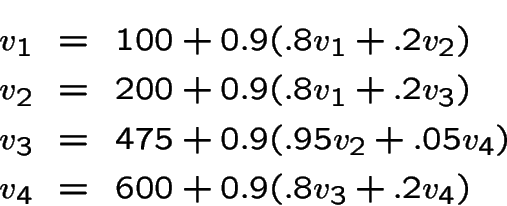
et
![$\color{red}{\bf v}=[1299,1465,1833,2341]$](img57.gif)
la solution optimale!
Le modèle n'est pas très réaliste (tous les
accidents mineurs n'ont pas le même coût)
mais ce calcul peut aider à prendre de bonnes décisions,
par exemple en l'état
![]() déclarer un sinistre si le coût
est supérieur à
déclarer un sinistre si le coût
est supérieur à
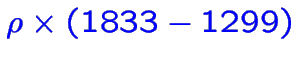 .
.