

Next: About this document ...
PROGRAMMATION LINEAIRE
(sujet des prochaines 3-4 semaines)
Maximiser (ou minimiser) une valeur qui dépendent de plusieurs variables
étant donné des contraintes sur ces variables
Quelques exemples:
- stocks+entrepôts : il faut avoir assez de chaque produit pour pouvoir
satisfaire aux demandes prévisibles; les entrepôts ont une capacité finie;
on veut minimiser le coût.
- produits+matières de base : chaque produit nécessite certaines quantités
des plusieurs matières de base; on ne peut pas en utiliser plus que l'on a;
on veut maximiser le profit.
- réseaux : le flux dans chaque arête ne peut pas être supérieur à
sa capacité; ce qui arrive à un noeud doit en partir; on veut minimiser
le coût d'un ensemble de flux qui effectue les transferts souhaités.
Définition générale
Un ensemble de variables:
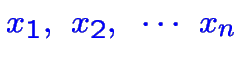
Une fonction objective linéaire à maximiser (ou minimiser):
Un ensemble de contraintes linéaires:
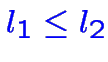 ,
,
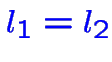 ,
,
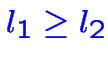 (chaque
(chaque
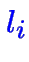 de la forme de
de la forme de
 )
il suffit de considérer des contraintes du premier type avec
)
il suffit de considérer des contraintes du premier type avec
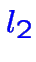 une constante:
une constante:
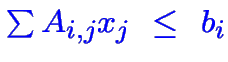
(Chaque
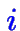 donne une contrainte; par convention
donne une contrainte; par convention
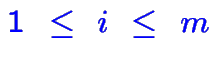
on écrit aussi maximiser
 avec
avec
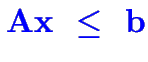
chaque contrainte correspond à une ligne de la matrice
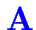 )
)
Forme canonique
- Chaque variable est astreinte à être
supérieure ou égale à

- Une restriction qui ne change rien quant à la difficulté du problème
- Mais souvent utile
Quelques définitions et cas spéciaux
-
solution réalisable; un ensemble de valeurs des variables vérifiant toutes les
contraintes
-
problème faisable; un problème qui possède au moins une solution réalisable
- problèmes sans borne finie sur la fonction objective:
c'est-à-dire le maximum
de la fonction objective (sur les solutions réalisables) n'existe pas.
- problème possédant plusieurs solutions optimales; (plusieurs ensembles
de valeurs des variables donnant la même valeur optimale de la fonction objective).
Exemple de solution sans borne
maximiser
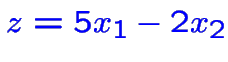
parmi les solutions sont:
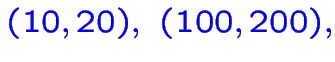
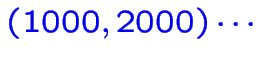 avec valeurs de
avec valeurs de
 :
:
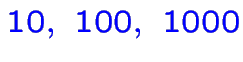 et ainsi de
suite.
et ainsi de
suite.
Exemple de plusieurs solutions optimales
maximiser
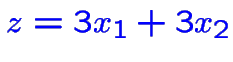
parmi les solutions sont:
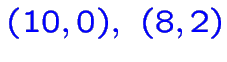 avec valeur de
avec valeur de
 :
:
 .
.
S'il existe
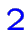 solutions optimales, il en existe un nombre infini:
solutions optimales, il en existe un nombre infini:
par exemple
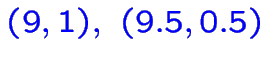
Exemple sans aucune solution réalisable
(En effet, on voit que la somme des deux dernières contraintes
divisée par
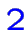 est
est
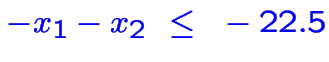 en contradiction avec la première.
en contradiction avec la première.
Interprétation géométrique
- Les valeurs des
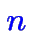 variables sont interprétées comme coordonnées d'un point
en
variables sont interprétées comme coordonnées d'un point
en
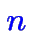 dimensions
dimensions
- Chaque contrainte définit un hyperplan dans cet espace tel que chaque solution
réalisable doit être à la même coté (ou sur) l'hyperplan
- polytope (+intérieur) de solutions réalisables (peut-être de dimension inférieure
à
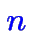 );
);
- convexité: La ligne droite reliant deux solutions réalisables consiste en d'autres
solutions réalisables
- si le polytope est fini, la fonction objective est bornée
Solutions de base
Une solution donnée par
la solution de
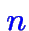 des équations correspondant aux contraintes
des équations correspondant aux contraintes
(c'est-à-dire les équations obtenues en remplacant
 par
par
 )
)
(à noter que si les
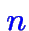 équations ne sont pas
indépendantes
la solution n'existe pas et elles ne donnent pas de solution de base)
équations ne sont pas
indépendantes
la solution n'existe pas et elles ne donnent pas de solution de base)
Un sommet du polytope
théorème : si la fonction objective est bornée, elle prend sa valeur optimale
à une solution de base
Donc un algorithme possible:
calculer chaque solution de base;
vérifier qu'elle est réalisable;
si oui calculer la fonction objective;
prendre le maximum des valeurs calculées.
Mais ca serait très très lent ...
Limitations:
Des contraintes réelles qu'on ne peut pas exprimer (directement)
par des contraintes linéaires.
- impossible de contraindre les variables à des valeurs
entières;
la ``programmation linéaire en nombres entiers'' a ses propres méthodes
- valeurs négatives: pas de problème (équivalence des
formes
canonique et générale);
[valeurs négatives; contraintes
 ,
,
 ; contraintes
; contraintes
 ]
]
- contraintes non-linéaires: impossible! (p.ex
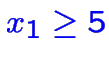 ou
ou
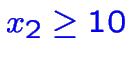 ,
,
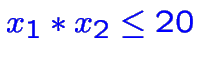 ...)
...)
- contraintes avec
 ou
ou
 (donc interdisant l'égalité):
pas mal de différence théoriquement, très peu pour nous.
(donc interdisant l'égalité):
pas mal de différence théoriquement, très peu pour nous.


Next: About this document ...
Mike ROBSON
2001-10-04
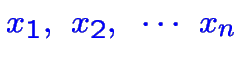
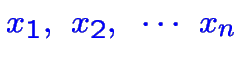
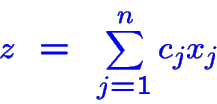
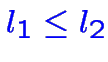 ,
,
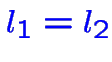 ,
,
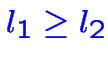 (chaque
(chaque
![]() de la forme de
de la forme de
![]() )
il suffit de considérer des contraintes du premier type avec
)
il suffit de considérer des contraintes du premier type avec
![]() une constante:
une constante:
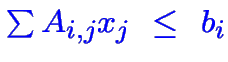
![]() donne une contrainte; par convention
donne une contrainte; par convention
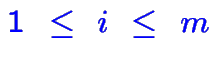
![]() avec
avec
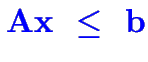
![]() )
)
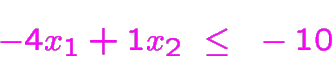
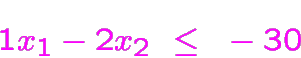
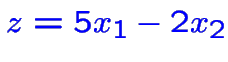
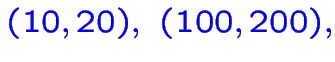
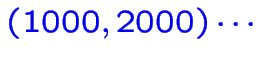 avec valeurs de
avec valeurs de
![]() :
:
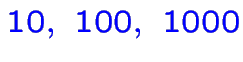 et ainsi de
suite.
et ainsi de
suite.
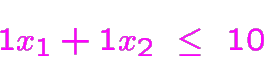
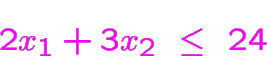
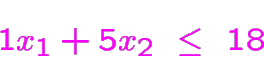
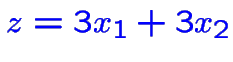
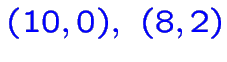 avec valeur de
avec valeur de
![]() :
:
![]() .
.
![]() solutions optimales, il en existe un nombre infini:
solutions optimales, il en existe un nombre infini:
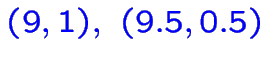
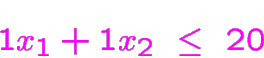
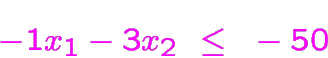
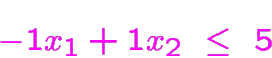
![]() est
est
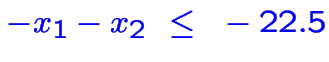 en contradiction avec la première.
en contradiction avec la première.
![]() des équations correspondant aux contraintes
des équations correspondant aux contraintes
![]() par
par
![]() )
)
![]() équations ne sont pas
indépendantes
la solution n'existe pas et elles ne donnent pas de solution de base)
équations ne sont pas
indépendantes
la solution n'existe pas et elles ne donnent pas de solution de base)
 ]
]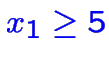 ou
ou
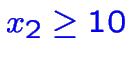 ,
,
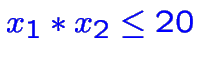 ...)
...)