Algorithme efficace pour résoudre des problèmes de programmation linéaire
(ou de trouver qu'il n'y a pas de solution)
Beaucoup utilisé et réussit sur les problèmes ``réels''
Théoriquement trop lent pour des problèmes très bizarres
Basé sur deux idées importantes:
Chaque arête parcourue augmente la fonction objective: donc pas de boucles
Le nombre de sommets est fini: donc terminaison garantie
Pas de maximaux locaux qui ne sont pas de maximaux globaux: donc l'algorithme ne peut se terminer qu'à une solution optimale (s'il y en a)
Comment est-ce que ça s'arrête?
Aucun sommet voisin avec une valeur supérieure de
![]()
On a trouvé la valeur optimale (si elle existe)
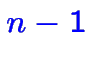 parmi elles
parmi elles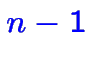 et une nouvelle équation
et une nouvelle équation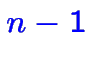 des équations actuelles et une nouvelle
peut échouer (aucune solution ou plusieurs solutions
ou pas réalisable ou valeur pas améliorée)
des équations actuelles et une nouvelle
peut échouer (aucune solution ou plusieurs solutions
ou pas réalisable ou valeur pas améliorée)
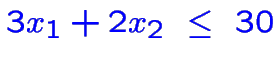
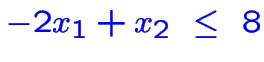
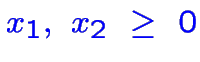
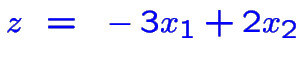 à maximiser.
à maximiser.
La solution de base
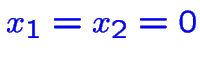 est réalisable avec
est réalisable avec
![]() .
Les solutions voisines sont obtenues en supprimant une des équations
.
Les solutions voisines sont obtenues en supprimant une des équations
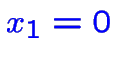 ou
ou
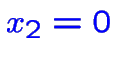 et en ajoutant une des équations
et en ajoutant une des équations
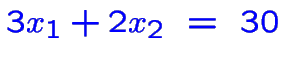 ou
ou
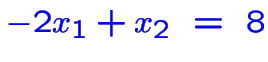
Donc quatre possibilités:
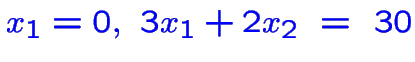 :
:
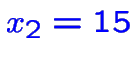 n'est pas réalisable.
n'est pas réalisable.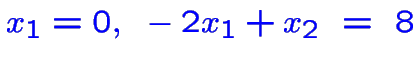 :
:
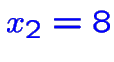 réalisable avec
réalisable avec
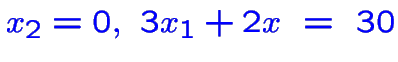 :
:
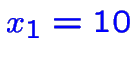 réalisable avec
réalisable avec
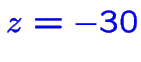 .
.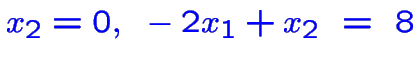 :
:
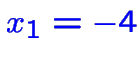 n'est pas réalisable.
n'est pas réalisable.
On continue de la solution:
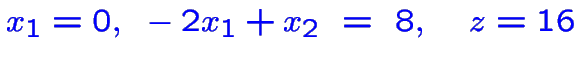 .
.
Supprimer une des équations:
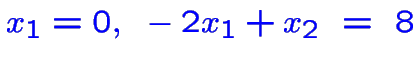
Ajouter une équation choisie parmi
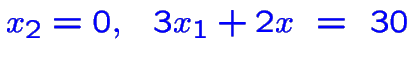
En fait on ne trouve qu'une nouvelle solution:
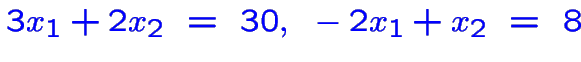 :
:
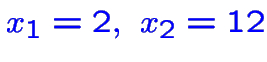 réalisable avec
réalisable avec
![]() , donc une amélioration.
, donc une amélioration.
Et ainsi de suite (mais pour ce petit exemple il n'y a plus de possibilités d'amélioration).
On a fait 3 itérations et pour chaque itération
on calcule 4 voisins; donc 12 sommets calculés
sur les 6 qui existent!
Mais pour un exemple de taille raisonnable c'est mieux:
10 variables et 10 contraintes explicites: 184756 sommets
Si l'algorithme prend 40 itérations (un peu pessimiste),
on n'en calcule que
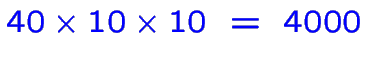 .
.
(Et on va voir que le vrai algorithme fait encore moins de calcul)
Plus la taille du problème est élevée, plus cette méthode gagne par rapport à la méthode très naïve de calculer toutes les solutions de base.
On considère d'abord le cas où
 est une
solution de base réalisable
et l'algorithme part de là:
est une
solution de base réalisable
et l'algorithme part de là:
On va supprimer une seule des équations
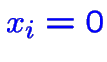 ; donc cette
variable
; donc cette
variable
![]() va devenir positive et les autres resteront nulles.
Donc, il faut choisir une variable à coefficient positif en
va devenir positive et les autres resteront nulles.
Donc, il faut choisir une variable à coefficient positif en
![]() .
.
En choisir une (peut-être mais pas forcément celle au coefficient le plus élevé?)
Chaque contrainte avec un coefficient
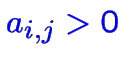 donne une borne
supérieure sur la nouvelle valeur de
donne une borne
supérieure sur la nouvelle valeur de
![]() ;
;
Choisir la plus petite de ces bornes; c'est la contrainte qu'il faut rajouter.
Une astuce algébrique permet de continuer à faire les calculs de la même façon efficace
Transformer le problème en ``forme standard''.
C'est la forme où les seules contraintes sont que chaque variable est positive ou nulle et des contraintes dans la forme d'équations. La transformation s'effectue en ajoutant une nouvelle variable ``variable d'écart'' pour chaque contrainte d'inéquation:
Par exemple
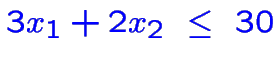 devient
devient
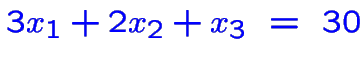 où
où
![]() est la variable d'écart, contrainte
d'être positive ou nulle.
est la variable d'écart, contrainte
d'être positive ou nulle.
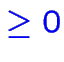 )
)
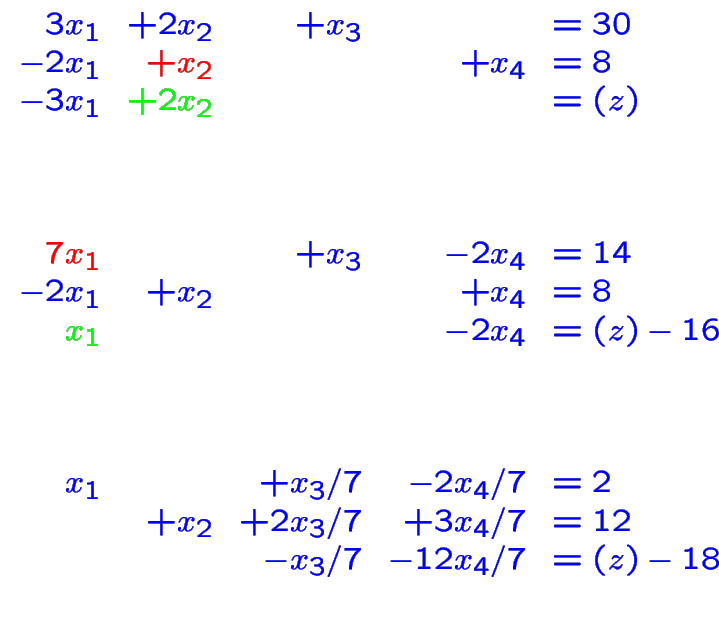
En pratique on garde les coefficients dans un tableau et supprime les
colonnes
connues ne contenir qu'un élément non nul etc. mais ce ne sont que
des
détails de programmation.