Je veux entrer dans l'état
(Equivaut à maximiser la probabilité d'être dans un état cible d'une chaîne de Markov à un moment donné de l'avenir)
Supposons que dans un graphe orienté
![]() donné, à un instant pair
je choisis l'état successeur mais à un instant impair le choix
est aléatoire (et disons uniforme);
donné, à un instant pair
je choisis l'état successeur mais à un instant impair le choix
est aléatoire (et disons uniforme);
Je veux entrer dans l'état
![]() à l'instant
à l'instant
![]() .
.
Mes choix à l'instant
![]() sont évidents (et dépendent
de l'état après
sont évidents (et dépendent
de l'état après
![]() ),
),
donc, je peux calculer ma probabilité de réussite en fonction de
l'état avant
![]() ),
),
donc, mes choix à
![]() sont évidents,
sont évidents,
et ainsi de suite jusqu'à mes choix à
![]() .
.
J'utilise un tableau qui, pour chaque instant (entre ![]() et
et ![]() ) et
chaque état me
donnera
la probabilité de réussite si je suis en cet état à cet
instant;
) et
chaque état me
donnera
la probabilité de réussite si je suis en cet état à cet
instant;
Les éléments de ce tableau sont reliés par une récurrence.
Je remplis le tableau itérativement.
Le résultat souhaité est déterminé facilement du tableau final.
Facile à généraliser à optimiser l'espérance de la valeur du sommet final si chaque sommet a une valeur.
le temps de calcul aurait été déterminé par le nombre de
chemins
de longueur entre ![]() et
et ![]() dans le graphe;
dans le graphe;
sans doute des siècles de calcul
que la programmation dynamique a réduits à une fraction d'une seconde.
Etant donné un sac à dos et plusieurs ![]() objets de poids et valeur
différents, quel est la valeur maximum d'un ensemble d'objets qui ne
dépasse
pas ma capacité de le porter?
objets de poids et valeur
différents, quel est la valeur maximum d'un ensemble d'objets qui ne
dépasse
pas ma capacité de le porter?
Supposons que je considère les objets en ordre et décide, pour chacun, si je le prends ou non;
quand je considère l'objet numéro ![]() , la valeur de ce que je
pourrai choisir parmi
, la valeur de ce que je
pourrai choisir parmi 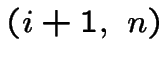 dépend de la partie non utilisée
de ma capacité
dépend de la partie non utilisée
de ma capacité
je calcule pour chaque ![]() et chaque poids (entre
et chaque poids (entre ![]() et ma capacité
initiale) une valeur maximum
et ma capacité
initiale) une valeur maximum
Le tableau me donne immédiatement la réponse à la question
et facilement un ensemble qui réussit cette valeur maximum.
Un algorithme très efficace si les poids sont des entiers et ma capacité n'est pas trop importante (exprimée dans la même unité)
Pas évident comme calcul; pas de récurrence directe.
Mais si j'ajoute un deuxième paramètre la taille de la plus grande partie je trouve une récurrence:
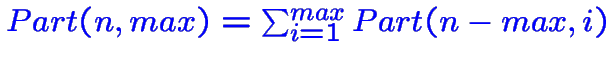
sauf dans les cas 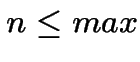
Le temps pour visiter les derniers ![]() villes dépend de quelles
villes elles sont et d'où il se trouve après la
villes dépend de quelles
villes elles sont et d'où il se trouve après la 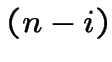 ième
visite
ième
visite
La programmation dynamique ne donne pas d'algorithme très performant mais aucun meilleur n'est connu qui garantit de donner toujours le parcours optimal.
Quand la récurrence donne la valeur de la colonne ![]() du tableau comme
fonction de la colonne
du tableau comme
fonction de la colonne 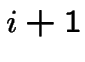 (ou
(ou 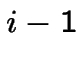 ) on n'est pas obligé de
garder tout le tableau; il suffit de garder deux colonnes à chaque
moment.
) on n'est pas obligé de
garder tout le tableau; il suffit de garder deux colonnes à chaque
moment.
Si, en outre, chaque élément d'une colonne ne dépend que des éléments de l'autre colonne qui sont en dessus (ou en dessous), il suffit de garder une colonne qui, à chaque moment, peut contenir un partie de l'ancienne colonne et une partie de la nouvelle!
En ce cas, la programmation dynamique comme décrite fait des calculs inutiles qui n'auraient pas été faits par la méthode récursive citée avant. Mais il est toujours vrai que cette méthode récursive fait beaucoup plus de calculs parce qu'elle fait souvent le même calcul plusieurs fois.
Il existe une méthode mixte qui ne fait que les calculs utiles et ne les fait qu'une fois: elle consiste à utiliser la structure récursive et un tableau; la première fois qu'un résultat est calculé il est inséré dans le tableau; les fois suivants, cette valeur est récupérée du tableau.
Nécessite une méthode de savoir quels éléments du tableau contiennent des résultats valables; ou une valeur impossible pour les non valables ou un tableau auxiliaire booléen.