Pour le programme linéaire:
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
- 4 points
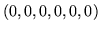 n'est pas une solution
réalisable.
Donnez un programme auxiliaire qui aide à la recherche d'une
solution réalisable de base. Quelle est une solution
réalisable de base de votre programme auxiliaire?
n'est pas une solution
réalisable.
Donnez un programme auxiliaire qui aide à la recherche d'une
solution réalisable de base. Quelle est une solution
réalisable de base de votre programme auxiliaire? - 2 points Quel est le dual du programme initial?
- 2 points
Du fait que
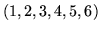 est une solution réalisable du programme
initial avec valeur
est une solution réalisable du programme
initial avec valeur 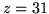 , que pouvez-vous déduire sur les
solutions
réalisables du dual?
, que pouvez-vous déduire sur les
solutions
réalisables du dual? - 2 points
Du fait que
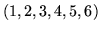 et
et 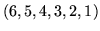 sont deux solutions
réalisables du programme initial, avec valeurs
sont deux solutions
réalisables du programme initial, avec valeurs 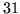 et
et 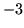 de la
fonction objective
de la
fonction objective 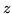 , déduisez une autre solution réalisable
et expliquez pourquoi elle ne pourrait pas être optimale.
, déduisez une autre solution réalisable
et expliquez pourquoi elle ne pourrait pas être optimale.
(Dans votre raisonnement vous n'utiliserez pas directement ni les contraintes ni la fonction objective.)
Dans les questions suivantes, quand un exemple d'un type de chaîne de Markov est demandé, il faut donner un exemple non-trivial, c'est-à-dire oú le comportement de la chaîne n'est pas complètement évident sans aucune analyse.
- 2 points Donnez un exemple d'une chaîne de Markov irréductible et apériodique et expliquez comment vous trouvez un système d'équations pour calculer sa distribution limite.
- 3 points
Donnez un exemple d'une chaîne de Markov possédant
au moins
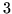 classes finales et expliquez comment vous trouvez
un système d'équations
pour calculer la probabilité de finir dans une classe
finale donnée à partir d'un état initial.
classes finales et expliquez comment vous trouvez
un système d'équations
pour calculer la probabilité de finir dans une classe
finale donnée à partir d'un état initial. - 3 points Donnez un exemple d'une chaîne de Markov possédant
une seule classe finale qui est périodique avec période
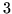 et expliquez comment vous trouvez
un système d'équations pour calculer la probabilité asymptotique
d'être dans une sous-classe donnée de cette classe après un
nombre
de transitions qui est multiple de
et expliquez comment vous trouvez
un système d'équations pour calculer la probabilité asymptotique
d'être dans une sous-classe donnée de cette classe après un
nombre
de transitions qui est multiple de 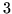 à partir d'un état initial.
à partir d'un état initial. - 2 points Donnez un algorithme pour décider dans une chaîne possédant une classe finale, si les états de cette classe sont périodiques et pour déterminer leur période.