


Next: About this document ...
INTRODUCTION
- Nom: J. M (Mike) Robson;
robson@labri.u-bordeaux.fr
- Emploi du temps: le plus souvent 2 heures de cours ou 2 heures de TD par semaine
- fichiers de transparents:
\http://dept-info.labri.u-bordeaux.fr/~robson/
transparents/RO/cours1.dvi etc.
- contrôle continu ?
- R.O. branche de math; à voir avec décisions économiques
- traitée ici d'une façon peu rigoureuse mais ...
- livres:
Techniques mathématiques de la Recherche opérationnelle, vol 5
Graphes et Programmation Linéaire: M. Sakarowitch ****
Recherche Opérationnelle: A. Henry-Labordère et M. Grojnowski
Linear Programming: V. Chvatal
- souvent en langue anglaise ...
Matières: techniques mathématiques de décision;
- où est la difficulté de prendre une décision?
- C'est plus difficile quand il s'agit de plusieurs décisions
dépendantes?
interaction entre mes décisions
- ou de décisions de politique à appliquer dans le long terme
interaction entre mes décisions d'aujourd'hui et celles de l'avenir
- ou de décisions dans un monde nondéterministe
interaction entre mes décisions et la nature
- techniques qui dépendent de la construction d'un modèle:
la solution donnée par une de ces techniques mathématiques n'est plus valable que notre
modèle!
PROGRAMMATION LINEAIRE
(sujet des prochaines 3-4 semaines)
Maximiser (ou minimiser) une valeur qui dépendent de plusieurs variables
étant donné des contraintes sur ces variables
Quelques exemples:
- stocks+entrepôts : il faut avoir assez de chaque produit pour pouvoir
satisfaire aux demandes prévisibles; les entrepôts ont une capacité finie;
on veut minimiser le coût.
- produits+matières de base : chaque produit nécessite certaines quantités
des plusieurs matières de base; on ne peut pas en utiliser plus que l'on a;
on veut maximiser le profit.
- réseaux : le flux dans chaque arête ne peut pas être supérieur à
sa capacité; ce qui arrive à un noeud doit en partir; on veut minimiser
le coût d'un ensemble de flux qui effectue les transferts souhaités.
Définition générale
Un ensemble de variables:
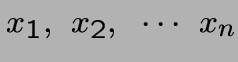
Une fonction objective linéaire à maximiser (ou minimiser):
Un ensemble de contraintes linéaires: 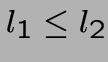 ,
l1 = l2,
,
l1 = l2,
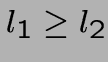 (chaque li de la forme de z)
il suffit de considérer
(chaque li de la forme de z)
il suffit de considérer
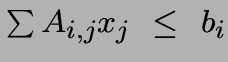
(Chaque i donne une contrainte; par convention
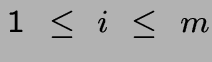
on écrit aussi maximiser 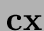 avec
avec 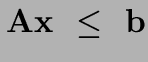
chaque contrainte correspond à une ligne de la matrice 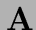 )
)
Forme canonique
- Chaque variable est astreinte à être
supérieure ou égale à 0
- Une restriction qui ne change rien quant à la difficulté du problème
- Mais souvent utile
Quelques définitions
- solution réalisable; un ensemble de valeurs des variables vérifiant toutes les
contraintes
- problème faisable; un problème qui possède au moins une solution réalisable
- problème possédant une solution optimale; un problème où le maximum (...)
de la fonction objective (sur les solutions réalisables) existe.
- problème possédant plusieurs solutions optimales; (plusieurs ensembles
de valeurs des variables donnant la même valeur optimale de la fonction objective).
- problèmes sans borne finie sur la fonction objective.
Interprétation géométrique
- Les valeurs des n variables sont interprétées comme coordonnées d'un point
en n dimensions
- Chaque contrainte définit un hyperplan dans cet espace tel que chaque solution
réalisable doit être à la même coté (ou sur) l'hyperplan
- polytope (+intérieur) de solutions réalisables (peut-être de dimension inférieure
à n);
- convexité: La ligne droite reliant deux solutions réalisables consiste en d'autres
solutions réalisables
- si le polytope est fini, la fonction objective est bornée
Solutions de base
Une solution où n des équations correspondant aux contraintes sont
satisfaites
(c'est-à-dire les équations obtenues en remplacant  par =)
par =)
Un sommet du polytope
théorème : si la fonction objective est bornée, elle prend sa valeur optimale
à une solution de base
Donc un algorithme possible:
calculer chaque solution de base;
vérifier qu'elle est réalisable;
si oui calculer la fonction objective;
prendre le maximum des valeurs calculées.
Mais ca serait très très lent ...
Limitations:
Des contraintes réelles qu'on ne peut pas exprimer (directement)
par des contraintes linéaires.
- impossible de contraindre les variables à des valeurs entières; pas forcément très grave;
- valeurs négatives: pas de problème (équivalence des
formes
canonique et générale);
[valeurs négatives; contraintes
 ,
=; contraintes
,
=; contraintes  ]
]
- contraintes non-linéaires: impossible! (p.ex
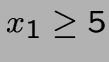 ou
ou
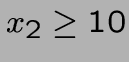 ,
,
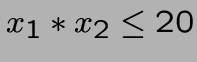 ...)
...)
- contraintes avec < ou > (donc interdisant l'égalité):
pas mal de différence théoriquement, très peu pour nous.



Next: About this document ...
Mike ROBSON
2000-10-04
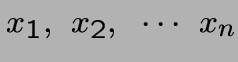
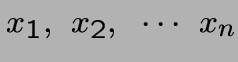
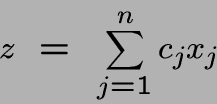
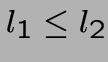 ,
l1 = l2,
,
l1 = l2,
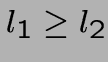 (chaque li de la forme de z)
il suffit de considérer
(chaque li de la forme de z)
il suffit de considérer
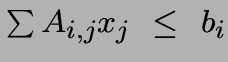
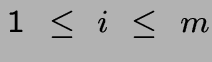
![]() avec
avec 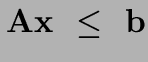
![]() )
)
![]() par =)
par =)
 ]
]
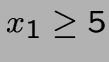 ou
ou
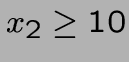 ,
,
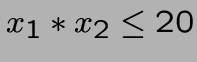 ...)
...)