


Next: About this document ...
Deux problèmes avec la méthode du simplexe
- Comment commencer?
Il faut commencer à une solution de base réalisable;
(ou trouver qu'il n'y en a pas)
mais la réussite de la méthode dépend du fait qu'on peut
éviter de regarder toutes les solutions de bases potentielles.
- Terminaison prématurée ou boucle infinie
Dans un cas la méthode ``supprimer une équation et en ajouter
une nouvelle'' ne trouve aucune solution meilleur quand on n'est
pas à la solution optimale.
Trouver une solution de base pour commencer
- Modifier le problème de sorte que le nouveau problème aie une solution
de base triviale et une solution optimale du nouveau
problème soit forcément une solution
réalisable (de base) de l'ancien;
- Résoudre ce nouveau problème par
l'algorithme du simplexe!
- Enfin commencer a résoudre le vrai problème
- Pour construire le nouveau problème:
- Ajouter une nouvelle variable, disons y (avec
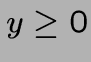 )
)
- Remplacer toute contrainte
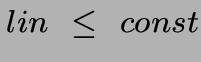 par
par
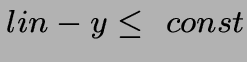 (et transformer dans la forme canonique)
(et transformer dans la forme canonique)
- Il existe une solution réalisable de base avec n+1
équations vérifiéses
- Minimiser y (maximiser -y); si le résultat est nul, on a trouvé une solution
réalisable de base
de l'ancien problème; sinon il n'y en a pas.
Un petit exemple
Les contraintes:
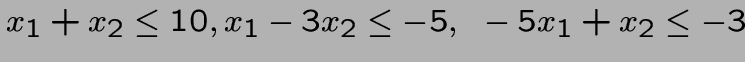 deviennent
deviennent
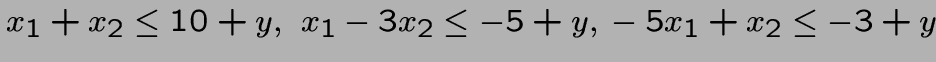
et le problème avec
ces contraintes et la fonction objective
z = -y
a la solution réalisable de base x1=x2=0,
x1-3x2= -5+y
Une solution optimale est
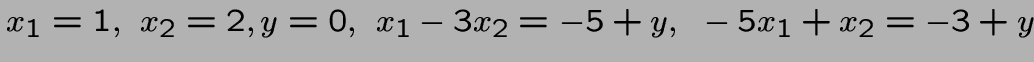
Donc
x1=1, x2=2,, x1-3x2= -5,
5x1+x2= -3 est une solution réalisable
de base du vrai problème.
Et les équations vérifiées à cette solution du vrai problème
se trouve en supprimant le y= 0 dans les équations de la
solution optimale du problème auxiliaire!
Amélioration nulle
Comment? Si le nombre d'équations des contraintes vérifiées à
une solution est supérieure à n.
Une itération jette une contrainte et en ajoute une autre;
ça peut donner la même solution.
Et l'algorithme pourrait boucler (même point; ensembles différents
d'équations).
Mais il existe au moins un bon ensemble d'équations
qui permet à l'algorithme
de continuer (vraie amélioration de z
s'il y en a).
Donc,
- 1.
- choisir les équations à supprimer et à rajouter comme normale avec
un choix aléatoire quand plus d'un candidat
marche de façon acceptable quand il existe une meilleur
solution mais ne peut pas trouver qu'il n'y en a pas.
- 2.
- ajouter (virtuellement) une petite quantité
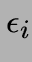 à la constante bi de la contrainte i;
à la constante bi de la contrainte i;
Agir comme si
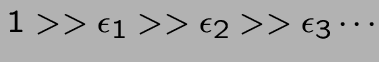 ;
;
Impossibilité d'avoir plus de n équations vérifiées!!
Et on résout un programme indistinguable de l'initial!
Pourquoi ne pas jeter les contraintes inutiles?
Trop difficile de les trouver!
Le ``vrai'' algorithme du simplexe de Dantzig
1
Calcul beaucoup plus vite de la première itération dans
le cas où
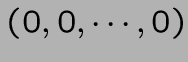 est une solution de base réalisable:
est une solution de base réalisable:
On va supprimer une seule des équations xi=0; donc cette
variable xi va devenir positive et les autres resteront nulles.
Donc, il faut choisir une variable à coefficient positif en z.
En choisir une (peut-être celle au coefficient le plus élevé?)
Chaque contrainte avec un coefficient ai,j>0 donne une borne
supérieure sur la nouvelle valeur de xi;
Choisir la plus petite de ces bornes; c'est la contrainte qu'il
faut rajouter.



Next: About this document ...
Mike ROBSON
2000-10-13
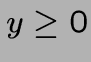 )
)
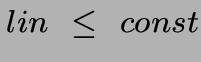 par
par
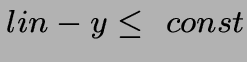 (et transformer dans la forme canonique)
(et transformer dans la forme canonique)
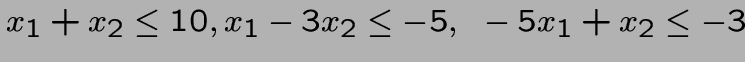 deviennent
deviennent
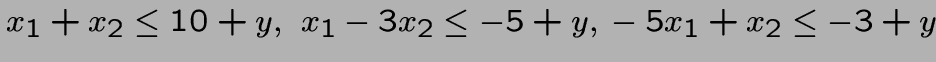
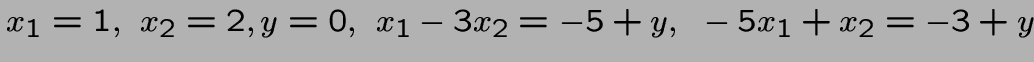
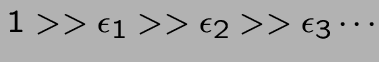 ;
;
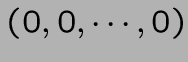 est une solution de base réalisable:
est une solution de base réalisable: