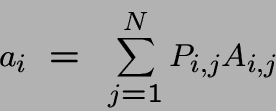
Coût d'une transition: Ai,j pour la transition de i à j (ne dépend pas du temps ni de l'histoire)
Coût moyen d'une transition: de l'état i:
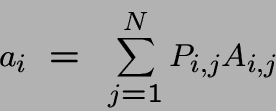
Coût moyen d'une suite de transitions de longueur n à partir de l'état i:
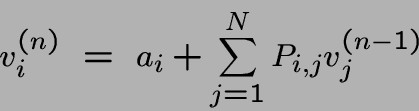
Tendance vers la moyenne
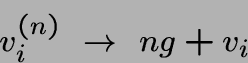
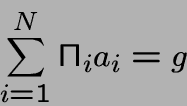
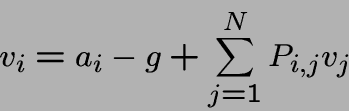
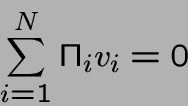
Les seules différences entre les états sont leurs valeurs de vi. En effet vi-vj est le prix raisonnable à payer pour changer de i à j.
La possibilité de choix: supposons que dans l'état i on peut choisir entre plusieurs décisions et que pour la décision d, la probabilité d'aller en état j est Pdi,j avec un coût adi,j
on peut calculer l'espérance du coût d'une transition:
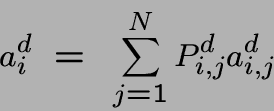
Une politique Markovienne est une règle qui détermine pour chaque état i, la probabilité de choisir chaque décision possible en cet état. Il existe une infinité (même non dénombrable) de politiques; il faut en choisir l'optimale!
Les politiques ``mixtes'' sont celles où dans un état i au moins deux décisions ont une probabilité non nulle. C'est bien connu dans la théorie des jeux qu'une politique mixte peut être supérieure à toute politique non mixte (stationnaire).
Ici, ça n'est pas le cas; il existe toujours une politique stationnaire optimale.
C'est pareil à la programmation linéaire où il y a toujours une solution
de base qui est optimale. Mais le nombre de politiques stationnaires peut
être trop grand pour calculer le coût de chacune.
Optimisation d'un système non-linéaire!
Le coût n'est pas une fonction linéaire des probabilités des choix.
Commencer à une politique stationnaire
(aucune difficulté pour la trouver)
Chercher des améliorations locales qui donnent une meilleure politique stationnaire:
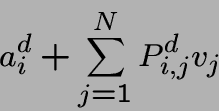
Répéter tant qu'il y a des améliorations possibles
Pourquoi amélioration?
un changement de politique réduit le coût pour cet état;
cette réduction peut réduire les coûts d'autres états
(mais pas les augmenter)
Pourquoi terminaison?
parce que amélioration à chaque étape et un nombre fini
de politiques stationnaires
Pourquoi optimal?? Supposons que d est calculée et d' est
optimale:
(a)
vid-vid' ne dépend pas de i
(b) on peut changer d à d' pour un état i,
en gardant les mêmes coûts
(c) ... et donc d et d' ont les mêmes coûts; d est aussi optimale.
Les choix possibles sont:
machine neuve: entretien normal:
entretien préventif:
machine usagée: entretien normal:
entretien minutieux:entretien super
machine en panne: remplacement;
révision générale.
Les probabilités de transition (et coûts associés) sont:
machine neuve:
entretien normal:
0 (-), 0.9 (100), 0.1 (300)
entretien préventif:
0.1 (500), 0.9 (500), 0 (-)
machine usagée:
entretien normal:
0 (-), 0.7 (150), 0.3 (350)
entretien minutieux:
0 (-), 0.8 (400), 0.2 (600)
entretien super:
0 (-), 0.9 (750), 0.1 (950)
machine en panne:
remplacement:
1 (5000), 0 (-), 0 (-)
révision générale:
0.1 (7500), 0.9 (2500), 0 (-).
Les coûts moyens en 1 étape sont 120, 500, 210, 440, 770, 5000 et 3000.
On part de la politique (1,1,1)

donc
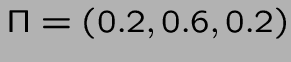
a = (120,210,5000) et donc g=1150.
v = ( -1200, - 483.33, 2650)
On décide une nouvelle politique de (2,2,2).
Par exemple, en l'état 1, le calcul
v1=120+0.9 x -483.33+0.1 x 2650 donne -50;
par contre la politique 2 donne
500+0.1 x -1200 + 0.9 x
-483.33 = -55
et la politique 2 est meilleure.

donc
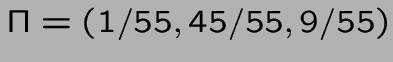
a = (500,440,3000) et donc g=860.
v = (-8100/11,-3700/11,19400/11)
On décide une nouvelle politique de (1,1,2).

donc
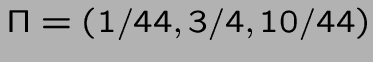
a = (120,210,3000) et donc g=37050/44
v = (-473625,-226125,793575)/484
calculé par
solve(v1=120+(9/10)*v2+v3/10-g,
v2=210+(7/10)*v2+(3/10)*v3-g,
v1/44+3*v2/4+10*v3/44=0);
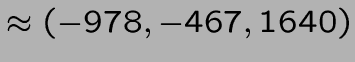
Aucune amélioration possible.