Version 2025-06
Licence CC–BY–NC–ND
TRANSFORMATION D'IMAGES
Christophe Schlick
schlick ಄ u-bordeaux • fr
L'objectif de cette feuille d'exercices est d'illustrer le principe de la transformation d'images par algorithmes. Les algorithmes de génération (présentés dans la feuille d'exercices A) permettent de créer une image en fonction d'un ensemble de paramètres numériques fournis par l'utilisateur, et destinés à contrôler le processus de création. A l'inverse, les algorithmes de transformation (présentés dans ce notebook) doivent impérativement partir d'une image existante qui servira de base pour la création de la nouvelle image. Il existe aujourd'hui un très grand catalogue d'algorithmes de transformations d'images permettant d'obtenir des effets visuels extrêmement variés, mais toutes ces techniques peuvent être classés en trois catégories principales :
- Transformations géométriques : La transformation appliquée à un pixel ne dépend que de sa position
- Transformations optiques : La transformation appliquée à un pixel ne dépend que de sa couleur
- Transformations par filtres : La transformation appliquée à un pixel dépend de sa position, de sa couleur, ainsi que des positions et des couleurs des pixels de son voisinage
Le package numpy pourrait évidemment être largement suffisant pour réaliser toutes les transformations d'images abordées dans cette feuille d'exercices. Néanmoins, le package Pillow fournit des outils de plus haut niveau, ce qui va grandement simplifier la plupart des opérations à mettre en oeuvre. Avant de commencer cette feuille d'exercices, il est donc fortement recommandé de relire le notebook 06-Pillow.ipynb qui contient les éléments de cours correspondants.
import numpy as np # import du package 'numpy' avec alias 'np'
import PIL.Image as pim # import du module 'Image' du package 'Pillow' avec alias 'pim'
import PIL.ImageOps as pio # idem avec module 'ImageOps'
import PIL.ImageChops as pic # idem avec module 'ImageChops'
import PIL.ImageFilter as pif # idem avec module 'ImageFilter'
import PIL.ImageDraw as pid # idem avec module 'ImageDraw'
from SRC.tools import show, view # import de deux fonctions du module 'tools'
import warnings; warnings.filterwarnings('ignore') # on ignore les 'warnings'
Exercice C1 - Transformations géométriques
Ecrire les instructions Python permettant de générer les 8 images de la figure ci-dessous. Chaque image individuelle est obtenue en appliquant une transformation géométrique sur l'image du tigre utilisée dans le chapitre 6 du cours (la zone noire visible sur certaines images correspond à la taille initiale de l'image, soit 640x480 pixels). Les transformations mises en oeuvre pour les 8 images (de gauche à droite et de haut en bas) sont les suivantes :
- double symétrie (verticale et horizontale)
- contraction horizontale à 50%
- contraction uniforme à 50%
- dilatation uniforme à 1600% (+ recadrage autour de l'oeil droit du tigre)
- rotation de 15° (sans modification de la taille de l'image finale)
- rotation de 15° (avec ajustement de la taille de l'image finale)
- cisaillement horizontal
- déformation projective
Vous aurez besoin des méthodes suivantes, définies pour la classe pim.Image utilisée par Pillow (à vous de trouver le rôle de chaque méthode et celui de leurs paramètres) :
img.transpose(method)img.resize(size, method)img.crop(box)img.rotate(angle, expand)img.transform(size, method, data)

tiger = pim.open('IMG/tiger.jpg') # lecture du fichier 'tiger.jpg' (mode = 'RGB')
W, H = tiger.size # stockage de la taille de l'image (utile pour toutes les fonctions ultérieures)
# les méthodes possibles pour 'transpose' sont numérotés de 0 à 6, avec les alias suivants :
# FLIP_LEFT_RIGHT = 0 / FLIP_TOP_BOTTOM / ROTATE_180 / ROTATE_270 / ROTATE_90 / TRANSPOSE / TRANSVERSE = 6
img = tiger.transpose(pim.FLIP_LEFT_RIGHT) # application d'une symétrie horizontale
#img = tiger.transpose(pim.ROTATE_180) # application d'une rotation de 180°
#img = tiger.transpose(pim.TRANSPOSE) # application d'une transposition (rotation 90° + symétrie verticale)
# les méthodes possibles pour 'resize' sont numérotés de 0 à 5, avec les alias suivants :
# NEAREST = 0 / BOX / BILINEAR / BICUBIC / HAMMING / LANCZOS = 5
# Pour la contraction d'image (= dézoom), le mode BOX est à privilégier
#img = tiger.resize((W//2, H), pim.BOX) # contraction horizontale (mode BOX)
#img = tiger.resize((W//2, H//2), pim.BOX) # contraction dans les 2 directions (mode BOX)
# Pour la dilatation d'image (= zoom), le mode LANCZOS est à privilégier
w, h = W//16, H//16; x, y = 265, 155 # définition de la taille et de la position pour la zone à découper
zone = tiger.crop((x, y, x+w, y+h)) # découpage de la zone autour de l'oeil droit
#img = zone # affichage de la zone découpée
#img = zone.resize((W,H), pim.BOX) # dilatation (mode BOX)
#img = zone.resize((W,H), pim.LANCZOS) # dilatation (mode LANCZOS)
view(img) # affichage de l'image finale
img = tiger.rotate(15) # rotation de 15 degrés (sans modification de la taille de l'image)
#img = tiger.rotate(15, expand=True) # idem avec expansion de l'image pour ne pas perdre d'information
# les méthodes possibles pour 'transform' sont numérotés de 0 à 4, avec les alias suivants :
# AFFINE = 0 / EXTENT / PERSPECTIVE / QUAD / MESH = 4
# le mode QUAD est le plus intuitif : il suffit de définir les coordonnées des 4 points
# qui vont se retrouver aux 4 coins dans l'image finale (ordre = NW, SW, SE, NE)
data = (0,0, 0,480, 640,480, 640,0) # paramètres pour une transformation à l'identique
#data = (0,480, 0,0, 640,0, 640,480) # paramètres pour une symétrie verticale
#data = (640,0, 0,0, 0,480, 640,480) # paramètres pour une rotation à 90° + dilatation horizontale
#data = (-160,0, 0,480, 800,480, 640,0) # paramètres pour un effet de cisaillement
#data = (-160,-160, -40,520, 640,640, 800,-60) # paramètres pour un effet de perspective
#data = (0,-480, 0,960, 640,260, 640,220) # paramètres pour une rotation à 180°
#img = tiger.transform((W,H), pim.QUAD, data=data) # application de la transformation choisie
view(img) # affichage de l'image finale
Exercice C2 - Découpages et collages
Ecrire les instructions Python permettant de générer les 8 images de la figure ci-dessous. Chaque image individuelle est obtenue en appliquant une transformation géométrique, de type découpage et/ou collage, sur les images du tigre et du smiley. Les transformations mises en oeuvre pour les images (de gauche à droite et de haut en bas) sont les suivantes :
- collage périodique d'un rectangle noir
- extraction de la partie gauche de l'image, puis collage avec symétrie horizontale
- extraction de la tête du tigre, puis collage périodique horizontal et vertical
- collages multiples avec redimensionnement et rotation
- découpage de l'image en 12 blocs de 160x160 pixels, puis collage avec permutation aléatoire des blocs
- incrustation d'un smiley au niveau de l'oeil droit du tigre
- incrustation de 25 smileys avec des positions aléatoires sur l'image
- incrustation de 12 smileys, avec des positions aléatoires dans des blocs de 160x160 pixels
En plus des méthodes de l'exercice C1, vous aurez besoin des méthodes suivantes :
img.new(mode, size, color)img.paste(image, coords)

img = tiger.copy() # création du réceptacle pour le collage (= copie de l'image 'tiger')
w, h = W//40, H; bar = pim.new('1', (w,h), 0) # création d'une image pour les barreaux (couleur = noir)
for p in range(2*w, W, 7*w): img.paste(bar, (p, 0)) # collage des barreaux sur l'image de départ
#img = pim.new('RGB', (W,H)) # création du réceptacle pour le collage (= image noire, par défaut)
#w, h = W//2, H; x, y = 60, 0 # définition des paramètres (taille et position) pour le découpage
#tile = tiger.crop((x, y, x+w, y+h)) # découpage de la zone de gauche de l'image
#img.paste(tile); img.paste(tile.transpose(0), (w, 0)) # collage avec symétrie horizontale
#img = pim.new('RGB', (W,H)) # création du réceptacle pour le collage
#m, n = 3, 2; w, h = W//m, H//n # définition des paramètres (m*n tuiles)
#tile = tiger.resize((w,h), pim.BOX) # redimensionnement de la tuile avant collage (= déformation)
#XY = [(i*w, j*h) for i in range(w) for j in range(n)] # calcul des positions des n*n tuiles
#for x,y in XY: img.paste(tile, (x,y)) # boucle de collage pour les m*n tuiles
#img = pim.new('RGB', (W,H)) # création du réceptacle pour le collage
#m, n = 3, 2; w, h = W//m, H//n; x, y, step = 124, 0, min(m,n) # définition des paramètres (m*n tuiles)
#tile = tiger.crop((x, y, x + step*w, y + step*h)) # découpage de la tuile dans l'image initiale
#tile = tile.resize((w,h), pim.BOX) # redimensionnement de la tuile avant collage (= sans déformation)
#XY = [(i*w, j*h) for i in range(m) for j in range(n)] # calcul des positions des m*n tuiles
#for x,y in XY: img.paste(tile, (x,y)) # boucle de collage pour les m*n tuiles
#img = pim.new('RGB', (W,H)) # création du réceptacle pour le collage
#w, h = 256, 192; x, y = 90, 11 # définition des paramètres pour le découpage et le collage
#tile# = tiger.resize((w, h), pim.BOX) # redimensionnement de la tuile avant collage
#img.paste(tile, (x, y)); img.paste(tile.transpose(3), (x+y+h, y+w+y)) # tigres horizontaux
#img.paste(tile.transpose(2), (x, y+h+y)); img.paste(tile.transpose(4), (x+w+y, y)) # tigres verticaux
view(img) # affichage de l'image finale
img = pim.new('RGB', (W,H)) # création du réceptacle pour le collage
m, n = 4, 3; w, h = W//m, H//n # définition des paramètres pour les tuiles
oldXY = [(i*w, j*h) for i in range(m) for j in range(n)] # calcul des positions des m*n tuiles
newXY = oldXY[:] # positions finales pour les 12 tuiles (copie de la liste précédente)
np.random.shuffle(newXY) # mélange aléatoire des positions finales
for (ox,oy),(nx,ny) in zip(oldXY, newXY): # parcours simultané des positions initiales et finales
img.paste(tiger.crop((ox, oy, ox+w, oy+h)), (nx,ny)) # collage de la tuile à sa nouvelle position
smiley = pim.open('IMG/smiley.png') # lecture du fichier 'smiley.png' (mode = 'RGBA')
WS, HS = smiley.size # stockage de la taille de l'image du smiley (utile pour la suite)
#img = tiger.copy(); img.paste(smiley, (240, 120)) # collage avec la zone blanche autour du smiley
#R, G, B, A = smiley.split(); view(R); view(G); view(B); view(A) # visualisation des 4 canaux R/G/B/A
# on peut enlever la zone blanche autour du smiley en utilisant le canal A comme masque pour le collage
#img = tiger.copy(); img.paste(smiley, (240, 120), mask=smiley) # collage sans la zone blanche
#img = tiger.copy(); n = 25 # 'n' définit le nombre de smileys à coller
#XY = np.random.randint(0, (W-WS,H-HS), (n,2)) # calcul des positions aléatoires pour les collages
#for x,y in XY: img.paste(smiley, (x,y), mask=smiley) # boucle de collage pour les 'n' smileys
# on fait une première version où les smileys sont collés au centre de chaque case d'une grille
# régulière (4 colonnes, 3 lignes). Chaque case a une taille de 160x160 (= 640/4 et 480/3)
# img = tiger.copy(); m, n = 4, 3; w, h = W//m, H//n # 'm x n' définit la grille des smileys à coller
# XY = np.indices((m,n)).reshape(2,m*n).T * (w,h) # positions initiales des m*n collages
# XY += ((w-WS)//2, (h-HS)//2) # ajout d'un décalage pour placer chaque collage au centre de la zone
# for (x,y) in XY: img.paste(smiley, (x,y), mask=smiley) # boucle de collage pour les 'm x n' smileys
# il ne reste plus qu'à rajouter une perturbation aléatoire à la position de chacun des 12 collages
# img = tiger.copy(); m, n = 4, 3; w, h = W//m, H//n # 'm x n' définit la grille des smileys à coller
# XY = np.indices((m,n)).reshape(2,m*n).T * (w,h) # positions initiales des m*n collages
# XY += ((w-WS)//2, (h-HS)//2) # ajout d'un décalage pour placer chaque collage au centre de la zone
# dw, dh = WS//3, HS//3 # amplitude de la pertubation aléatoire appliquée aux positions des collages
# XY += np.random.randint((-dw,-dh), (dw+1,dh+1), (m*n,2)) # ajout de la perturbation aléatoire
# for (x,y) in XY: img.paste(smiley, (x,y), mask=smiley) # boucle de collage pour les 'm x n' smileys
view(img) # affichage de l'image finale
Exercice C3 - Transformations optiques
Ecrire les instructions Python permettant de générer les 8 images de la figure ci-dessous. Chaque image individuelle est obtenue en appliquant une transformation optique (sur les canaux R/G/B) sur l'image du tigre utilisée dans le chapitre 6 du cours. Les transformations mises en oeuvre (de gauche à droite et de haut en bas) sont les suivantes :
- échange des canaux R et B
- combinaison linéaire des canaux RGB : $R' = 0.6R + 0.4G\;, G' = 0.2R + 0.8B\;, B' = B$
- combinaison barycentrique des canaux RGB : $L = 0.299R + 0.587G + 0.114B$
- inversion de l'image de luminance
- binarisation des valeurs de luminance
- binarisation des valeurs RGB
- quantification de la luminance sur 5 niveaux
- ajout de bruit puis quantification des valeurs RGB sur 3 niveaux
- assombrissement de l'image RGB
- éclaircissement de l'image de luminance
- augmentation du contraste de l'image RGB
- diminution du contraste de l'image de luminance
Toutes les transformations demandées peuvent s'effectuer en manipulant les images sous forme de matrice numpy

tiger = pim.open('IMG/tiger.jpg') # lecture du fichier 'tiger.jpg' (mode = 'RGB')
tigar = np.array(tiger) / 256 # conversion en matrice 'numpy' avec valeurs dans [0,1[
img = tigar[:,:,(2,1,0)] # permutation des canaux RGB (échange R et B)
mat = [[0,0,1], [0,1,0], [1,0,0]] # idem avec matrice de changement de base
#img = tigar @ mat # application de la transformation par multiplication matricielle
mat = [[0.6,0.2,0.0], [0.4,0.0,0.0], [0.0,0.8,1.0]] # combinaison linéaire des canaux RGB
#img = tigar @ mat
mat = np.random.random((3,3)); mat /= np.sum(mat, axis=0) # combinaison aléatoire des canaux RGB
#img = tigar @ mat
mat = [[0.28,0.24,0.16], [0.56,0.48,0.32], [0.14,0.12,0.08]] # combinaison linéaire (= sepia)
#img = tigar @ mat
mat = [0.333, 0.333, 0.333] # combinaison barycentrique des canaux RGB (= niveaux de gris)
#img = tigar @ mat
mat = [0.299, 0.587, 0.114] # combinaison barycentrique pondérée par la perception (= luminance)
tigarL = tigar @ mat # création de l'image de luminance
#img = tigarL
#img = 1 - tigarL # inversion de l'image de luminance
view(img) # affichage de l'image finale
binarize = lambda t, s=0.5: t > s # fonction de binarisation avec seuil arbitraire
img = binarize(tigarL, 0.4) # binarisation avec seuil de 0.4
#img = binarize(tigar) # binarisation des canaux RGB (= solarisation) avec seuil par défaut
quantize = lambda t, n=2: t * n // 1 / (n-1) # quantification sur 'n' niveaux
#img = quantize(tigarL, 5) # quantification sur 5 niveaux de gris
#img = quantize(tigar, 4) # quantification RGB sur 4 niveaux (= effet sérigraphie)
noise = np.random.normal(0, 0.3, (H,W,1)) # génération d'un bruit monochrome à distribution normale
#img = tigar + noise # ajout du bruit sans recalibrage
#show("img.shape; img.min(); img.max()") # avant recalibrage, on sort de l'intervalle [0,1[
#img = np.clip(tigar + noise, 0, 0.999999) # on recalibre sur l'intervalle [0,1[
#show("img.shape; img.min(); img.max()") # après recalibrage, on ne sort plus de l'intervalle
#img = quantize(img, 3) # on rajoute une quantification sur 3 niveaux (= effet grain photo)
noise = np.random.normal(0, 0.2, (H//4,W//4,3)) # bruit polychrome à distribution normale (1/16e de l'image)
noise = noise.repeat(4,axis=0).repeat(4,axis=1) # on duplique chaque pixel du bruit sur un bloc 4x4
noise += np.random.uniform(-0.5, 0.5, (H,W,1)) # on ajoute une perturbation par un bruit uniforme monochrome
#img = noise # visualisation du bruit final (= polychrome basse fréquence + monochrome haute fréquence)
#img = np.clip(tigar + noise, 0, 0.999999) # on ajoute le bruit et on recalibre sur l'intervalle [0,1[
view(img) # affichage de l'image finale
# définition des deux versions de 'gain' (augmentation ou diminution de luminance)
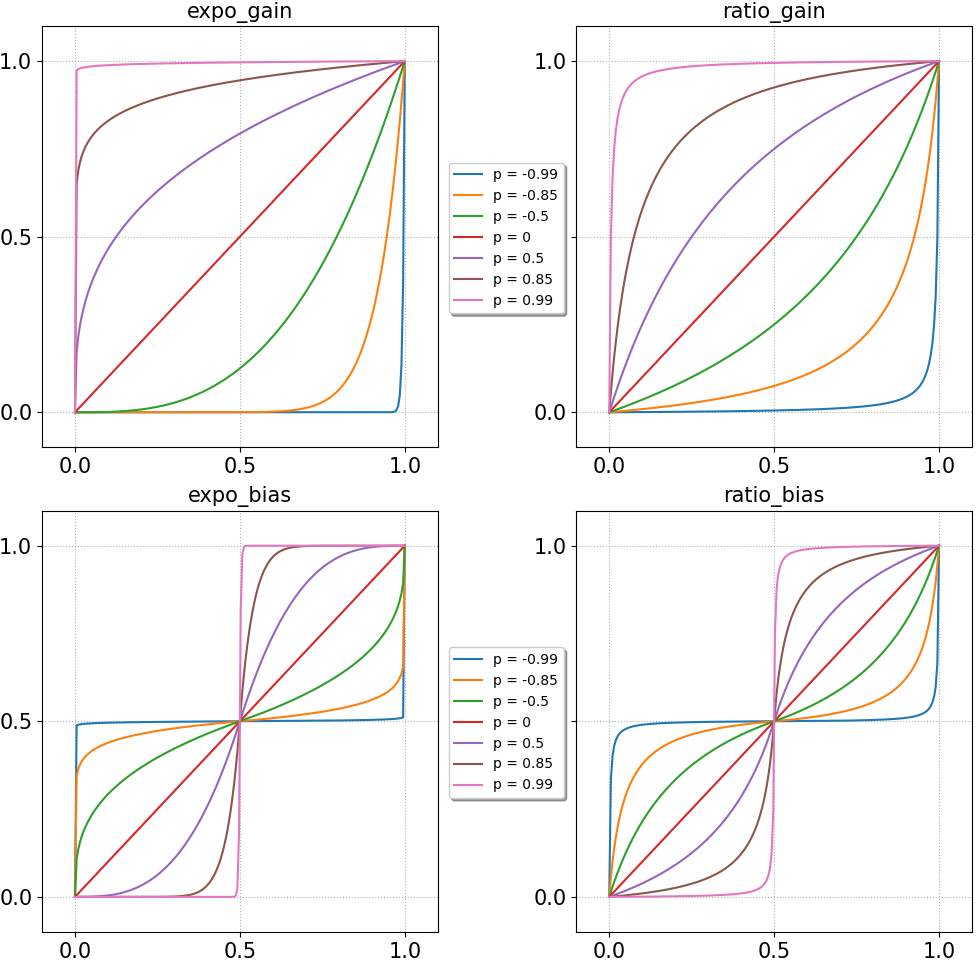
expo_gain = lambda t,p: t**((1-p)/(1+p))
ratio_gain = lambda t,p: (t+p*t)/(1-p+2*p*t)
# définition des deux versions de 'bias' (augmentation ou diminution de contraste)
expo_bias = lambda t,p: np.where(t < 0.5, 0.5*(2*t)**((1+p)/(1-p)), 1-0.5*(2-2*t)**((1+p)/(1-p)))
ratio_bias = lambda t,p: np.where(t < 0.5, (t-p*t)/(1+p-4*p*t), (t-2*p+3*p*t)/(1-3*p+4*p*t))
# note : le tracé des 4 fonctions pour différentes valeurs de 'p' se trouve sur la figure ci-dessous
img = ratio_gain(tigar, -0.5) # diminution de la luminance moyenne
#img = ratio_gain(tigarL, 0.7) # augmentation de la luminance moyenne
# note : tester les 2 versions 'ratio_gain' et 'expo_gain'
#img = ratio_bias(tigar, 0.6) # augmentation du contraste
#img = ratio_bias(tigarL, -0.8) # diminution du contraste
# note : tester les 2 versions 'ratio_bias' et 'expo_bias'
view(img) # affichage de l'image finale
# les transformations optiques sont beaucoup plus simple à réaliser avec 'numpy' qu'avec 'Pillow', mais
# si on veut absolument le faire avec 'Pillow' il faut passer par la fonction 'point' qui prend en entrée
# une fonction de transfert sur des entiers dans l'intervalle [0,255]. Voici quelques exemples :
tigerL = tiger.convert('L') # création de l'image de luminance (en mode 'Pillow')
# création d'une fonction de conversion entre les transformations optiques 'numpy' et 'Pillow'
# la fonction 'lut' permet de réutiliser les fonctions binarize, quantize, expo_gain, ratio_gain, etc...
lut = lambda func, p: lambda t: int(256*func(t/256, p))
bin = lut(binarize, 0.5) # fonction de binarisation avec seuil = 0.5
img = tigerL.point(bin) # # application de la fonction à l'image de luminance
#img = tiger.point(bin) # # application de la fonction à l'image RGB
step3 = lut(quantize, 3) # fonction de quantisation à 3 niveaux
#img = tigerL.point(step3) # application de la fonction à l'image de luminance
bias = lut(ratio_bias, -0.4) # fonction de diminution du contraste avec facteur 0.4
gain = lut(ratio_gain, 0.2) # fonction d'augmentation de luminance avec facteur 0.2
#img = tiger.point(bias).point(gain) # application des 2 fonctions à l'image RGB
view(img)
Exercice C4 - Filtres et convolutions
Ecrire les instructions Python permettant de générer les 8 images de la figure ci-dessous. Chaque image individuelle est obtenue en appliquant un filtre ou un noyau de convolution sur l'image du tigre. Selon les transformations à générer, on pourra utiliser soit les fonctions de Pillow, soit les fonctions de numpy. Les transformations mises en oeuvre pour les 8 images (de gauche à droite et de haut en bas) sont les suivantes :
- conservation d'un seul canal de couleur (R en haut, G au milieu, B en bas)
- coloration de l'image de luminance avec dégradé bleu vers orange
- pixelisation de l'image (blocs de 16x16 pixels)
- application d'un masque circulaire sur l'image
- test de quelques filtres prédéfinis (par exemple, rehaussement des contours)
- application d'un flou gaussien sur les yeux du tigre
- utilisation d'une combinaison de filtres (par exemple, détection des contours et soustraction)
- composition entre l'image initiale et sa version monochrome floutée, en fonction d'un masque circulaire

img = tigar.copy() # création d'une copy de travail (format 'numpy')
# on annule les 2 composantes inutiles dans chacune des 3 zones : G,B = (1,2) / R,B = (0,2) / R,G = (0,1)
img[:160,:,(1,2)] = img[160:320,:,(0,2)] = img[320:,:,(0,1)] = 0
# création d'une interpolation linéaire horizontale entre les couleurs [0,0.5,1] et [1,0.5,0]
ramp = np.tile(np.linspace([0,0.5,1], [1,0.5,0], 640), (480, 1, 1))
#img = ramp # visualisation de la rampe de couleurs obtenue
#img = ramp * tigarL[:,:,None] # application de la rampe de couleurs à l'image de luminance
#img = ramp * tigar # application de la rampe de couleurs à l'image RGB
#img = tigar[::16,::16,:].repeat(16, axis=0).repeat(16, axis=1) # pixelisation en blocs 16x16
t = np.linspace(-1, 1, 400); x, y = np.meshgrid(t, t)
mask = 1 - np.clip(x*x + y*y, 0, 1) ** 4 # génération du masque en forme de disque avec dégradé
#img = mask # visualisation du masque obtenu (400x400 pixels)
mask = np.pad(mask, ((50,30), (140,100))) # centrage du masque par rapport à la tête du tigre
#img = mask # visualisation du masque après centrage (640x480 pixels)
#img = tigar * mask[:,:,None] # application du masque en mode multiplicatif
view(img)
img = tiger.filter(pif.EDGE_ENHANCE) # filtre de rehaussement des contours
#img = tiger.filter(pif.EDGE_ENHANCE_MORE) # filtre de rehaussement des contours plus intense
#img = tiger.filter(pif.FIND_EDGES) # filtre de détection des contours
#img = tigerL.filter(pif.EMBOSS) # filtre d'embossage (= effet de relief)
#img = pio.invert(img) # idem avec inversion de la luminance (= inversion du relief)
#img = tiger.filter(pif.GaussianBlur(16)) # filtre de flou gaussien
#img = tiger.copy() # création d'une copie de travail
zone = (200,100,520,260) # definition de la zone à flouter
blur = tiger.filter(pif.GaussianBlur(16)) # génération de l'image floutée
#img.paste(blur.crop(zone), zone) # application du flou uniquement sur la zone définie
view(img)
base = tigerL.filter(pif.BLUR) # filtre de flou sur l'image de luminance
img = base # visualisation de l'image après application du filtre
#img = pic.subtract(tigerL, base, scale=0.05) # soustraction entre l'image et la version floutée
#img = pic.subtract(tiger, base.convert('RGB'), scale=0.1) # idem avec l'image RGB
base = tiger.filter(pif.EDGE_ENHANCE).filter(pif.FIND_EDGES) # filtre de détection de contours
#img = base # visualisation de l'image de luminance après application du filtre
#img = pic.subtract(tiger, base, scale=0.5) # soustraction entre l'image et l'image de contours
base = tigerL.point(step3).filter(pif.CONTOUR).convert('RGB') # quantification puis contourage
#img = base # visualisation de l'image de luminance après application du filtre
#img = pic.multiply(tiger, base) # application du masque en mode multiplicatif
#img = pic.multiply(tiger.point(step3), base) # idem avec quantification du tigre
mask = pim.new('L', (640,480)) # création d'une image noire pour le masque
pid.Draw(mask).ellipse((140,50,540,450), '#FFF') # ajout d'un disque blanc
#img = mask # visualisation du masque binaire (image noire avec disque blanc)
mask = mask.filter(pif.GaussianBlur(32)) # ajout de flou gaussien sur le disque
#img = mask # visualisation du masque monochrome après ajout de flou
base = tigerL.convert('RGB').filter(pif.GaussianBlur(6)) # création de la zone extérieure
#img = base # visualisation de la zone extérieure (image monochrome avec flou)
#img = pic.composite(tiger, base, mask) # composition des 2 images en fonction du masque
view(img)