Présentation¶
Le but de ce premier TD est de vous familiariser avec les réseaux de neurones et leur entraînement. Nous allons passer en revue les éléments de base suivant :
données d'apprentissage,
fonction de perte (loss function)
descente de gradient
Pour cela, nous allons utiliser un réseau de neurone (composé d'un seul neurone en fait) pour deux tâches :
une régression linéaire simple
une classification binaire.
Commençons par importer quelques unes des bibliothèques usuelles :
import numpy as np
import random as rd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
On génère les données¶
Afin de réaliser une régression linéaire simple, nous allongs générer un nuage de points. Exécutez le code de la cellule suivante :
#Data:
def generate(m, sizeNoise, slope, intersect):
x = [rd.random()*50 + 5 for i in range(m)]
noise = [rd.random() * sizeNoise for i in range(m)]#np.rand(m,1) * sizeNoise
y = [intersect + slope*x[i] + noise[i] for i in range(m)]
return np.array([x]), np.array([y])
m = 100
sizeNoise = 10
a = 0.8
b = 20
X, Y = generate(m, sizeNoise, a, b)
plt.grid()
plt.scatter(X, Y)
<matplotlib.collections.PathCollection at 0xffff56cc0250>
Exercice 1. Un neurone :¶
Comme vu en cours, un neurone formel est représenté comme suit :
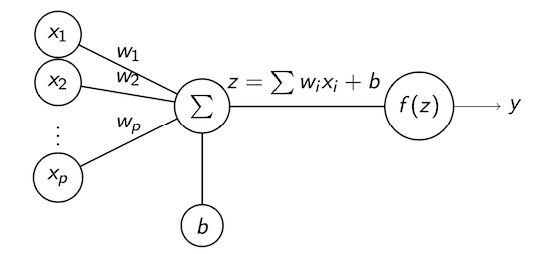
Nommez chacun des élements du neurone.
Ecrivez une fonction
neuron(x, w, b, f)permettant d'implémenter ce neurone.
- Définissez deux fonctions
idetsigmoiddéfinies par : $$ id(z) = z \mbox{ et } sigmoid(z) = \frac{1}{1+ e^{-z}}. $$
- Testez vos fonctions. L'exécution de la cellule suivante devrait donner le résultat affiché.
x = np.array([1])
w = np.array([1])
b = [1]
y_hat = neuron(x, w, b, id)
print('x: ', x)
print('y_hat: ', y_hat)
x: [1] y_hat: [2]
Exercice 2. Régression linéaire :¶
Dans cet exercice, nous allons entraîner un neurone pour réaliser une régression linéaire simple.
- Dessiner le neurone qui sera utilisé. Identifiez bien les paramètres à trouver.
- Ecrivez le code de la fonction
loss(y, y_hat)définie comme la moyenne des carrés des écarts :
$$ loss\left(y, \hat{y}\right) = \frac 1 {2*n} \sum_{i=1}^n \left(\hat{y_i} - y_i)\right)^2. $$
- Calculez le gradient de la fonction ${\cal L} = loss$ par rapport aux deux variables $w$ et $b$.
- Ecrivez la focntion
gradient(x, y_hat, y)retournant le gradient de la fonction $\cal L$.
- Ecrivez une fonction
train(x, y, eta, epochs)qui réalise une déscente du gradient de la fonction $\cal L$ afin de trouver les paramètres $w$ et $b$ minimisant la valeur de $\cal L$.
- Entraînez votre neurone. Prenez $0.001$ comme valeur pour le pas d'apprentissage, et $10000$ pour le nombre d'epochs.
- Donnez l'équation de la droite de régression obtenue. Ecrivez l'instruction permettant de calculer les valeurs prédites.
- Dessinez la droite de régression sur la même figure que le nuage de point.
- Comparez le résultat obtenu avec la droite donnée par
linregressdu sous modulestatsdu modulescipy.
Exercice 3. Régression logistique :¶
Dans cet exercice, nous allons transformer le neurone afin de l'utiliser pour réaliser une classification. Nous allons nous limiter à une classification bianire : les élements appartiennent soit à une classe 0 soit à une classe 1.
- Comment devons-nous appeler la "fonction"
neuronpour que le fonction d'activation soit la sigmoid ?
x: [[1 2 3]] y_hat: [0.88079708 0.95257413 0.98201379]
- Exécutez la cellule suivante pour générer les données, les découper en deux parties train et test, etc. Observez le résultat de la cellule.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(n_samples=1000, n_features=1, n_classes=2,
n_informative=1, n_redundant=0, n_repeated=0,
n_clusters_per_class=1)
X_train, X_test, y_train, y_test = train_test_split(X, y)
print(X_train.shape)
print(y_train.shape)
print(np.unique(y))
(750, 1) (750,) [0 1]
- Définissez la nouvelle fonction de perte. Nous allons utiliser la fonction cross_entropy vue en cours :
$$ \cal L = -\frac 1 n \sum_{i=1} \left(y_i\times \log\left(\hat{y}_i\right) + (1-y_i)\log(1-\hat{y}_i)\right) $$
- Ecrivez les expressions mathématiques de ce que calcule votre neurone.
- Calculez le gradient de $\cal L$ et écrivez la fonction correspondante.
Indication : la dérivée de la fonction sigmoid est : $\sigma'(z) = \sigma(z)\left(1 - \sigma(z)\right)$.
- Adaptez une fonction
train(x, y, nu, epochs)pour réaliser une déscente du gradient de la fonction $\cal L$ afin de trouver les paramètres $w$ et $b$ minimisant la valeur de $\cal L$.
- Exécutez la cellule suivante pour que vos calculs matriciels puissent se faire et entraînez votre neurone.
X_train = np.reshape(X_train, (X_train.shape[1], X_train.shape[0]))
print(X_train.shape)
print(y_train.shape)
- Evaluez votre modèle. Pour cela :
8.1. Exécutez la cellule suivante pour formater les données de test.
X_test = np.reshape(X_test, (X_test.shape[1], X_test.shape[0]))
8.2. Appliquez votre neurone aux données de test et observez le résultat obtenu.
8.3. Transformez les sorties en 0 et 1 :
8.4. Evaluez la qualité du modèle obtenu