Master Cryptologie et Sécurité Informatique, semestre 3
Complexité, devoir 2003
Un corrigé
est disponible en fin de document.
Exercice 1
Montrer que NP ≠ co-NP
implique NP ≠ PSPACE.
Exercice 2
On rappelle que SUBSET-SUM est le problème
de décision suivant :
étant donnés n entiers
x1
, … , xn
et un entier t, existe-t-il un sous-ensemble
I de
{1, … , n}
tel que
∑ xi
= t,
où i parcourt I ?
Montrer que le problème consistant à calculer I,
s'il existe, se réduit polynomialement au problème
de décision (il n'est donc pas plus difficile).
Conseil : on suppose donné un algorithme A
résolvant le problème de décision ;
donner un algorithme efficace B pour calculer
I en utilisant A
(qui joue le rôle d'un oracle,
on ne se préoccupe pas
de la complexité de A).
Exercice 3
Un graphe orienté G définit un jeu,
où les deux joueurs
déplacent à tour de rôle un jeton sur le graphe :
si le jeton est sur le sommet i,
le joueur choisit un arc
i → j,
et place le jeton sur le sommet j ;
c'est ensuite à son adversaire de jouer, etc.
Il est interdit de visiter deux fois
le même sommet, et le joueur qui se retrouve coincé,
faute de coup légal à jouer, a perdu.
|
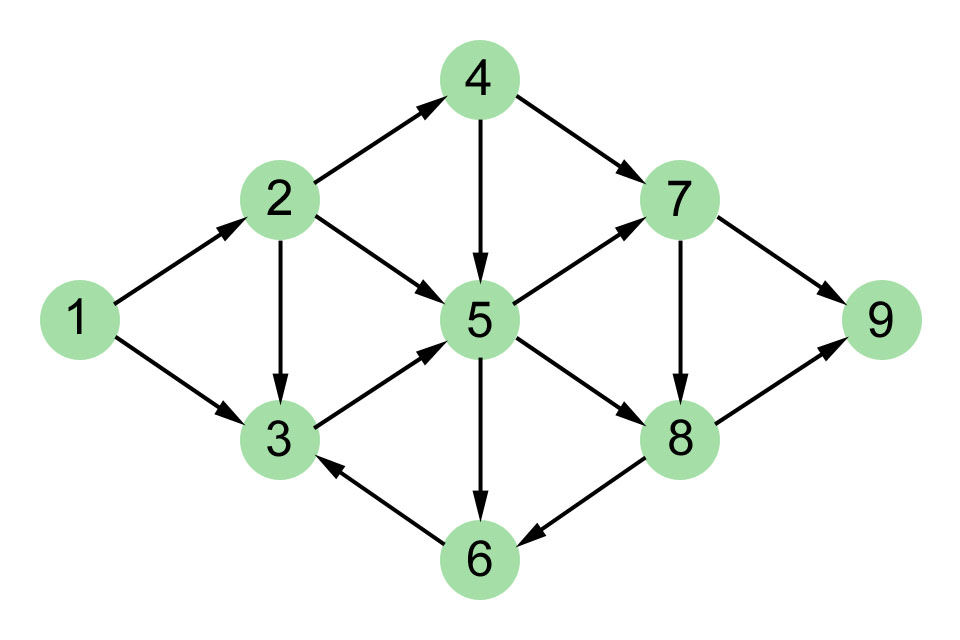
Exemple de partie, sur le graphe ci-contre,
si le sommet de départ est le sommet 1 :
le joueur I déplace le jeton en 2,
puis le joueur II le déplace en 5,
puis I choisit 8,
enfin II choisit 9, et I perd ;
si, dans un moment d'égarement, le joueur II
choisit 6 au lieu de 9 (à partir de 8),
I va en 3 (il n'a pas le choix)
et gagne, car le sommet 5 est déjà visité,
donc le joueur II est coincé en 3.
|
- Montrer que, dans le cas du graphe ci-dessus,
le joueur I (celui qui joue en premier)
a une stratégie gagnante si le sommet de départ est le sommet
numéro 1.
- Formuler un algorithme,
de complexité polynomiale en espace,
qui détermine si un sommet d'un graphe G
est ou non une position de départ
gagnante pour le joueur I.
- Appliquer cet algorithme pour déterminer
quels sont les sommets de départ gagnants
(respectivement perdants)
pour le graphe qui sert d'exemple ci-dessus.
Exercice 4
|
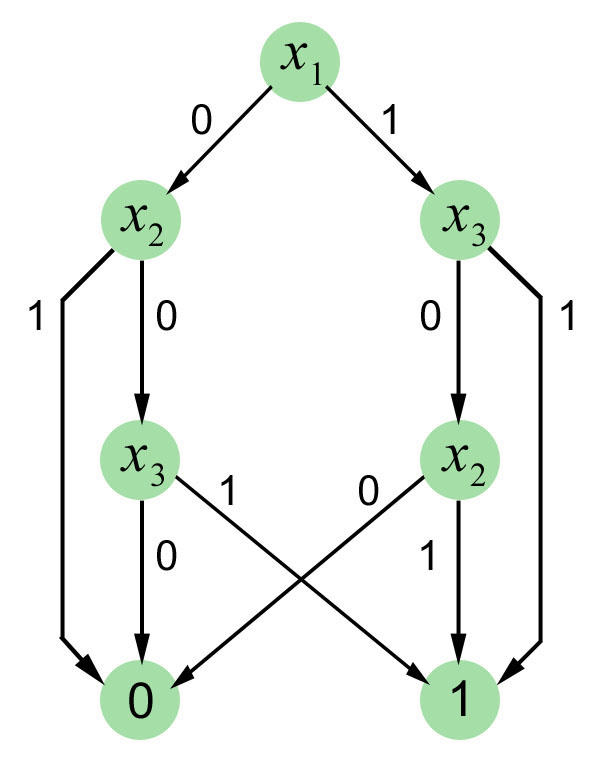
La figure ci-contre représente un
graphe acyclique (autrement dit sans cycle),
avec une racine unique (le sommet le plus
haut sur le dessin),
et deux feuilles étiquetées 0 et 1 ;
chaque sommet interne est étiqueté par une
variable booléenne, et deux arcs,
étiquetés 0 et 1, en sont issus.
A ce graphe est associé un
programme branché,
qui calcule une fonction booléenne Φ
des variables
x1
, … , xn
(ici n = 3),
de la façon suivante :
on entre par la racine, et
on suit l'arc étiqueté 0 ou 1 selon la valeur de
xi ;
l'étiquette du sommet final (sortie) détermine la valeur
de Φ pour ces arguments.
En outre ce programme est à lecture unique :
chaque variable apparaît au plus une fois sur tout chemin
joignant l'entrée à l'une des deux sorties.
|
|
- Donner la table de vérité de la fonction
calculée par ce programme, et donner sa
valeur en utilisant les opérateurs logiques
usuels (négation, conjonction, disjonction).
Le problème de l'équivalence de deux ROBP
(Read Once Branching Program) A et B
consiste à savoir s'ils calculent la même fonction
booléenne.
- Montrer que ce problème est dans co-NP.
Un algorithme probabiliste naïf consiste à choisir
aléatoirement chaque xi , et à répondre
"oui" si A et B calculent la même valeur,
"non" sinon.
- Etudier les probabilités de succès de cet
algorithme, dans chacun des cas
(A équivalent ou non à B).
Montrer qu'il existe des cas où la probabilité
d'erreur
de cet algorithme est excessive.
On construit un algorithme probabiliste efficace en associant
des polynômes p (
x1, … ,
xn )
à chaque sommet et à chaque arc du graphe,
de la façon suivante :
- le polynôme 1 est associé à l'entrée ;
- si p est associé
à un sommet étiqueté xi ,
le polynôme
( 1 - xi ) p
est associé à l'arc sortant étiqueté 0, et
xi p
est associé à l'arc sortant étiqueté 1 ;
- le polynôme associé à un sommet est la somme des
polynômes associés aux arcs entrants ;
- le polynôme associé à la sortie étiquetée 1
est celui associé au ROBP.
Pour tester si A et B sont équivalents,
on choisit aléatoirement
a1
, … , an
dans un corps fini F,
on évalue les polynômes associés
à A et B,
et on répond "oui" ou "non" selon que les valeurs
calculées coïncident ou pas.
- Calculer le polynôme associé au graphe
qui sert d'exemple ci-dessus
(on détaillera les calculs sur la copie).
- Etudier la complexité (en temps) de cet algorithme.
Note : la taille d'un ROBP
est la taille du graphe, qui est
proportionnelle au nombre de sommets.
- Montrer que si A et B sont équivalents,
l'algorithme répond toujours "oui".
- Dans le cas où
A et B ne sont pas équivalents,
on souhaite que
l'algorithme réponde "non"
avec une probabilité supérieure à 2/3. Quelle doit être
la taille #F du corps F ?
Pour la dernière question on aura besoin du lemme suivant,
qu'on admettra : la probabilité d'obtenir
p (
a1
, … , an ) = 0,
pour un polynôme donné p non nul,
où le degré de chaque variable est au plus d,
et pour un choix aléatoire
des ai dans F, est bornée par
n d / (#F) .
Exercice 1
Démontrons la contraposée, et supposons donc
NP = PSPACE ;
comme
co-NP ⊂
PSPACE,
on en déduit
co-NP ⊂
NP.
Or NP et co-NP
jouent des rôles symétriques, donc cette inclusion
entraîne l'inclusion inverse ;
pour le vérifier soit A un problème dans NP ;
le complémentaire A' de A
(la réponse au problème A' est positive
si la réponse au problème A est négative,
et vice-versa) appartient par définition
à co-NP, donc à NP,
puisque
co-NP ⊂
NP ;
mais alors le complémentaire de A',
qui n'est autre que A,
appartient à co-NP, ce qui prouve
l'inclusion
NP ⊂ co-NP.
Exercice 2
On suppose que
A ( {x1
, … , xn}, t ) = 1,
sinon
I = B
( {x1
, … , xn}, t )
n'est pas défini.
L'idée est de tester si x1
figure nécessairement dans le terme de gauche de l'égalité
∑ xi
= t,
en calculant
A ( {x2
, … , xn}, t ) ;
si le résultat de ce calcul vaut 0,
alors x1 est indispensable, d'où :
B ( {x1
, … , xn}, t ) =
{1} ∪
B ( {x2
, … , xn},
t - x1 )
sinon :
B ( {x1
, … , xn}, t ) =
B ( {x2
, … , xn}, t ).
Le cas particulier qui permet d'amorcer la récursion, est celui où
n = 0 :
A ( Æ , t )
= 1 si et seulement si t = 0 ,
B ( Æ , 0 )
= Æ
Cet algorithme récursif
peut facilement être transformé en
un algorithme itératif,
en notant par exemple
Xi =
{ xi , … , xn },
et X = X1 :
subset B (set X, int t) {
n = cardinal (X);
I = ensemble vide;
for (i = 1; i <= n; i++)
if ( ! A (Xi+1 , t) ) {
insérer i dans I;
t = t - X[i];
}
return I;
}
Note 1 : on utilise ci-dessus un formalisme
pseudo-C (qu'on pourrait transformer facilement
pour obtenir une vraie fonction C), mais toute
façon claire de décrire B
est satisfaisante ;
c'est le cas en particulier de la description récursive.
Note 2 : inutile de traiter à part
le cas i = n,
il suffit que la procédure qui calcule A
retourne le résultat correct
(à savoir 1 si
t = 0,
0 sinon)
lorsque le premier argument
est l'ensemble vide.
Variante :
l'algorithme itératif ci-dessus insère successivement
dans I les indices
des éléments indispensables à la
décomposition de t ;
on peut au contraire éliminer progressivement
de I les indices
des éléments non indispensables ;
d'où l'algorithme suivant, en notant
XI l'ensemble des
xi , pour i dans I :
subset B (set X, int t) {
n = cardinal (X);
I = {1, … , n};
for (i = 1; i <= n; i++) {
J = I - {i};
if ( A (XJ , t) )
I = J;
}
return I;
}
Exercice 3
- Stratégie gagnante pour
le joueur I,
si le sommet de départ est le sommet
numéro 1 : déplacer le jeton en 3 ;
le joueur II est forcé alors d'aller en 5,
et I va en 6, où son adversaire est coincé,
car le sommet 3 est déjà visité.
Une position dans un jeu est gagnante
(pour le premier joueur)
si et seulement si elle peut être
transformée en une position perdante
(c'est-à-dire non gagnante).
Voici l'algorithme, en pseudo-C :
int gagne (graphe G, int s) {
H = G privé de s;
pour chaque arc s → t dans G
if ( ! gagne (H, t) ) return 1;
return 0;
}
Note : lorsqu'on enlève le sommet s
du graphe,
on enlève évidemment tous les arcs dont une extrémité
(source ou but) est s.
Notons Gij…
le graphe G privé des sommets i, j, …
Exécution de gagne (G, 1) :
gagne (G, 1)
H = G1
Arc 1 → 2 :
|gagne (G1 , 2)
| H = G12
| Arc 2 → 3 :
| |gagne (G12 , 3)
| | H = G123
| | Arc 3 → 5 :
| | |gagne (G123 , 5)
| | | H = G1235
| | | Arc 5 → 6 :
| | | gagne (G1235 , 6)
| | | H = G12356
| | | Boucle non exécutée (pas d'arc issu de 6)
| | | return 0
| | |return 1 (stratégie 5 → 6)
| | Fin des arcs issus de 3
| |return 0 (la position 3 est perdante)
|return 1 (stratégie 2 → 3)
Arc 1 → 3 :
|gagne (G1 , 3)
| identique au calcul de gagne (G12 , 3)
| car il n'existe pas de chemin de 3 vers 2
| ...
|return 0 (la position 3 est perdante)
return 1 (stratégie 1 → 3)
On retrouve bien que la position de départ 1
est gagnante.
On a évalué aussi
gagne (G , 2),
car les graphes G et G1
sont équivalents de ce point de vue
(en partant de 2, on ne peut revenir en 1,
qui n'a que des arcs sortants) : la position
de départ 2 est gagnante.
De même on a évalué
gagne (G , 3),
la position
de départ 3 est perdante.
Exécution de gagne (G, 4) :
gagne (G, 4)
H = G4
Arc 4 → 5 :
|gagne (G4 , 5)
| H = G45
| Arc 5 → 6 :
| |gagne (G45 , 6)
| | H = G456
| | Arc 6 → 3 :
| | |gagne (G456 , 3)
| | | H = G3456
| | | Boucle non exécutée (pas d'arc issu de 3)
| | |return 0
| |return 1 (stratégie 6 → 3)
| Arc 5 → 7 :
| |gagne (G45 , 7)
| | H = G457
| | Arc 7 → 8 :
| | |gagne (G457 , 8)
| | | H = G4578
| | | Arc 8 → 6 :
| | | gagne (G4578 , 6)
| | | identique au calcul de gagne (G45 , 6)
| | | return 1 (stratégie 6 → 3)
| | | Arc 8 → 9 :
| | | gagne (G4578 , 9)
| | | H = G45789
| | | Boucle non exécutée (pas d'arc issu de 9)
| | | return 0
| | |return 1 (stratégie 8 → 9)
| | Arc 7 → 9 :
| | |gagne (G457 , 9)
| | | H = G4579
| | | Boucle non exécutée (pas d'arc issu de 9)
| | | return 0
| |return 1 (stratégie 7 → 9)
| Arc 5 → 8 :
| |gagne (G45 , 8)
| | identique au calcul de gagne (G457 , 8)
| |return 1 (stratégie 8 → 9)
|return 0
return 1 (stratégie 4 → 5)
La position de départ 4 est donc gagnante,
et on a vu au passage que la
position de départ 5 est perdante
(G et G4 sont équivalents
lorsqu'on part de 5).
La position de départ 6 est perdante : les mouvements
vers 3 puis 5 sont forcés, et le joueur I
se retrouve avec le choix entre
7 et 8, qui sont des positions
évidemment gagnantes, quels que soient
les sommets déjà visités, puisqu'il suffit d'aller en 9
(position de départ perdante par excellence).
Remarque : l'évaluation de
gagne (G, 8) découvre la curieuse stratégie
gagnante 8 → 6
(coup examiné avant le coup
gagnant 8 → 9), puis
6 → 3 → 5
→ 7 → 9
(tous les coups sont forcés).
Exercice 4
-
Table de vérité de Φ :
| x1 |
x2 |
x3 |
Φ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
|
Les lignes
2, 6, 7 et 8, pour lesquelles Φ vaut 1,
permettent d'écrire Φ en forme normale disjonctive.
La ligne 2 de la table correspond à la formule
¬x1
∧ ¬x2
∧ x3
et la ligne 6 à la formule
x1
∧ ¬x2
∧ x3 ;
ces deux lignes
ne diffèrent que par la valeur de x1,
donc la disjonction des deux formules vaut simplement
¬x2
∧ x3 .
De même les lignes 7 et 8 peuvent être résumées par
x1
∧ x2 , d'où une expression
en forme normale disjonctive :
Φ = (x1
∧ x2) ∨
(¬x2
∧ x3)
Pour obtenir
une forme normale conjonctive, il faut faire
les mêmes calculs pour les lignes
où Φ vaut 0 ;
on peut regrouper les lignes 1 et 5 :
x2
∨ x3
vaut 0 pour ces deux lignes, et elles seules ;
on regroupe aussi les lignes 3 et 4, d'où :
Φ = (x1
∨ ¬x2) ∧
(x2
∨ x3)
|
Note : si votre navigateur affiche mal les
expressions booléennes ci-dessus, mettez-le à jour ou
changez de navigateur ! Avec Internet Explorer sous
Windows XP, à la date (fin 2003) où est écrit ce document,
il "suffit de" choisir Options régionales et linguistiques
dans le panneau de configuration, puis, sous l'onglet
Langues : Installer les fichiers pour
les langues d'Extrême-Orient !
Les voies de Bill sont impénétrables.
Voici aussi une variante
du paragraphe ci-dessus, n'utilisant pas
les entités ¬ ∧ ∨
de la norme HTML.
- Le problème de l'équivalence de deux ROBP
A et B,
est dans co-NP,
car il existe un certificat
évident pour le problème complémentaire,
à savoir un vecteur de n
booléens pour lequel A et B
calculent des valeurs distinctes.
- Si A et B
sont équivalents, l'algorithme donne toujours
la bonne réponse (oui).
Mais si A et B
ne sont pas équivalents,
leurs tables de vérité peuvent différer
par une seule ligne,
et dans ce cas l'algorithme donne la bonne réponse (non)
avec la probabilité 1 / 2n .
Il faudra donc, dans ce cas, répéter en moyenne 2n
fois le test pour obtenir une preuve que A et B
ne sont pas équivalents :
autant comparer systématiquement leurs tables de vérité.
Trois chemins, d'étiquettes respectives
001, 101 et 11 mènent à la sortie étiquetée 1,
d'où le polynôme :
p = (1 - x1)
(1 - x2) x3
+
x1
(1 - x3) x2
+ x1 x3
En développant, on obtient :
p = x1 x2
- x2 x3
+ x3 =
x1 x2 +
(1 - x2) x3
et l'on reconnaît la forme normale
disjonctive obtenue pour Φ, question 1.
Note : le terme forme normale,
employé couramment dans ce contexte, est trompeur,
car cette forme cesse d'être unique
dès que l'on regroupe plusieurs lignes de la table
de vérité pour simplifier l'expression ;
c'est par chance (et parce que le nombre
de variables est très petit),
qu'on a obtenu le même
résultat ici et à la question 1.
-
Pour évaluer le polynôme associé à un ROBP,
il faut calculer les éléments de F
associés à chaque sommet et à chaque arc :
- on obtient la valeur associée à un
sommet en additionnant les valeurs
associées aux arcs entrants ; donc le nombre
total d'additions effectuées pour calculer
les valeurs associées aux sommets,
est égal au nombre d'arcs ;
- on obtient la valeur associée à un
arc en multipliant la valeur associée au sommet
source de l'arc, par ai
ou par
( 1 - ai ),
soit une opération élémentaire par arc.
On en déduit que le nombre total d'opérations nécessaires à
cette évaluation,
est proportionnelle au nombre d'arcs,
qui est lui-même le double du nombre de sommets
internes (c'est-à-dire autres que les sorties).
L'algorithme probabiliste,
qui effectue les évaluations pour chacun des deux ROBP,
puis les compare, est donc de complexité
λ m,
où m désigne la taille des données
(les deux ROBP), et λ le coût
d'une opération dans F ;
la question 7 montre que la taille de F
est une fonction linéaire du nombre n de variables,
donc la complexité de l'algorithme est polynomiale
(et même quasi-linéaire).
Note : la taille du polynôme
associé à un ROBP est en général une fonction
exponentielle de la taille du ROBP,
puisque le polynôme comporte un terme pour chaque
chemin de l'entrée vers la sortie
(étiquetée 1) ;
il ne faut surtout pas calculer ce polynôme avant
de l'évaluer.
Il faut prouver que
si A et B sont équivalents,
c'est-à-dire ont même table de vérité,
les polynômes associés sont identiques.
Chacun d'entre eux est formé, par construction,
d'une somme de produits,
et chaque produit
est associé à un chemin de l'entrée vers la sortie
(étiquetée 1) ;
chacun de ces produits est du type
y1…yn ,
où chaque yi vaut
xi ,
ou
( 1 - xi ) ,
ou 1 (si le chemin correspondant ne passe pas
par un sommet étiqueté
xi ).
En remplaçant chaque yi
égal à 1 par la somme
xi +
( 1 - xi ) ,
puis en développant,
on ne change pas le polynôme,
mais on obtient une somme de produits
comportant exactement un terme (et un seul)
pour chacune des lignes de valeur 1
dans la table de vérité associée au ROBP
(cf. question 1).
Donc les polynômes associés à deux ROBP équivalents
sont égaux.
Exemple : le polynôme obtenu en réponse
à la question 4 :
p = (1 - x1)
(1 - x2) x3
+
x1 x2
(1 - x3)
+ x1 x3
s'écrit aussi,
en remplaçant x1 x3
par x1
( x2 + 1 - x2 )
x3 :
p = (1 - x1)
(1 - x2) x3
+
x1 x2
(1 - x3)
+ x1 x2 x3
+ x1 (1 - x2)
x3
et chacun des 4 termes de la somme
correspond respectivement
aux lignes 001, 110, 111 et 101
de la table de vérité (question 1),
pour lesquelles Φ = 1 .
Dans le cas où
A et B ne sont pas équivalents,
la différence q des deux polynômes associés est non nulle,
et le degré de chaque variable est au plus 1 ;
donc en choisissant
#F ≥ 3n,
la probabilité d'obtenir la réponse "oui",
qui est égale à la probabilité d'avoir
malencontreusement choisi
pour a1…an
une solution de l'équation
q (
a1
, … , an ) = 0,
est bornée par 1/3,
d'après le lemme inclus dans l'énoncé.
Note : ce lemme
est une généralisation
du résultat classique, selon lequel un polynôme
à une variable,
de degré d, possède au plus d
racines dans un corps ; il se démontre par récurrence
sur le nombre n de variables.
La constante 2/3 qui figure dans
l'énoncé est arbitraire, et peut être remplacée par
n'importe quelle constante comprise (strictement) entre
0 et 1. Avec
#F ≥ 3n,
la probabilité d'erreur (obtenir une réponse "oui" erronée)
est bornée par 1/3,
donc en itérant k fois l'algorithme,
la probabilité d'erreur est bornée par
1/3k ;
mais même avec une probabilité d'obtenir la
bonne réponse ("non")
égale à 1/10 (au lieu de 2/3),
donc avec une probabilité d'erreur de 9/10
(borne garantie dès que
#F ≥ 10 n / 9 ),
l'algorithme reste efficace, pour la même raison ;
simplement dans ce dernier cas, il faudra en moyenne
10 itérations (au lieu de 1.5)
pour découvrir que
A et B ne sont pas équivalents.
L'algorithme probabiliste étudié dans cet exercice,
établit que le problème de l'équivalence de deux ROBP
appartient à la classe co-RP ;
la classe RP est constituée des problèmes
de décision pour lesquels il existe un algorithme
probabiliste tel que
la réponse "oui" soit sûre,
tandis que la réponse "non" peut être erronée,
mais avec une probabilité inférieure à une constante
e < 1 ;
ici les rôles des réponses "oui" et non" sont échangés.
On a :
P ⊂ RP
⊂ NP
La première inclusion est évidente,
et pour la seconde un tirage aléatoire
fournissant la réponse "oui" est un certificat.
On conjecture qu'en fait
P = RP.

