TP 2 - Parcours d'un graphe
L'objectif de ce TP est de compléter le module de graphe en ajoutant un affichage graphique pour les gaphes, des algorithmes de parcours en largeur et en profondeur et un algorithme de calcul de plus courts chemins.
Exercice 1
Appliquer l'algorithme du parcours en largeur
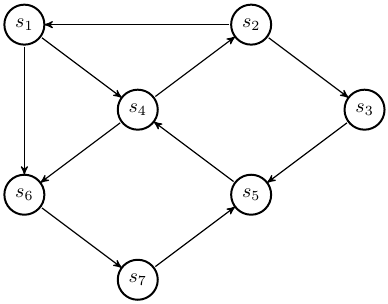
PL(G, s) au graphe F de la figure 1 à partir du sommet 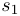 .
Vous donnerez à chaque fois l'ordre d'entrée des sommets dans la file.
.
Vous donnerez à chaque fois l'ordre d'entrée des sommets dans la file.
Pour rappel, le parcours en largeur est l'algorithme suivant:
PL(G, s)
pour chaque sommet u de X[G] - {s} faire
couleur[u] <- BLANC
d[u] <- infini
pere[u] <- nil
couleur[s] <- GRIS
d[s] <- 0
pere[s] <- nil
Enfiler(F, s)
tant que non vide(F) faire
u <- tete(F)
pour chaque v de Adj(u) faire
si couleur[v] = BLANC
alors couleur[v] <- GRIS
d[v] <- d[u] + 1
pere[v] <- u
Enfiler(F, v)
Defiler(F)
couleur[u] <- NOIR
Exercice 2
Implémentez le parcours en largeur.
Exercice 3
Calculer les plus courts chemins du graphe $G_1$ à partir du sommet $s_1$.
Implémentez une fonction qui calcule les plus courts chemins à partir d'un sommet donné.
Exercice 4
Qu'est-ce que l'accessibilité d'un sommet.
Pour le graphes de la figure 1, calculez les sommets accessibles depuis chaque sommet.
Ajouter à votre module de graphe un fonction permettant de calculer les sommets accéssibles depuis chaque sommet.
Exercice 5
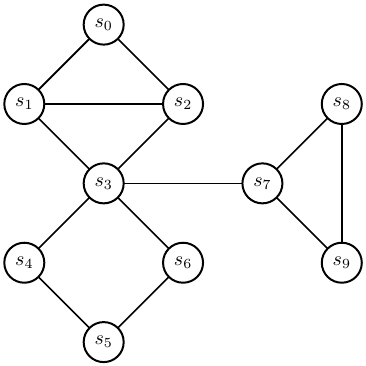
Appliquer l'algorithme de parcours en profondeur PP au graphe G de la figure 2.
Nous rappelons que le parcours en profondeur est l'algorithme suivant:
PP(G)
pour chaque sommet u de X faire
couleur[u] <- BLANC
pere[u] <- nil
temps <- 0
pour chaque sommet u de X faire
si couleur[u] = BLANC alors
Visiter_PP(u)
où Visiter_PP est défini par:
Visiter_PP(u)
couleur[u] <- GRIS
d[u] <- temps <- temps + 1
pour chaque v de Adj[u] faire
si couleur[v] = BLANC alors
pere[v] <- u
Visiter_PP(v)
couleur[u] <- NOIR
f[u] <- temps <- temps + 1
Implémentez le parcours en profondeur.
Exercice 6
Rapellez la définition d'un cycle.
Est-ce que le graphe de la figure 2 possède un cycle ?
Donnez un algorithme simple pour détecter si un graphe possède un cycle.
Ajouter à votre module de graphe un fonction permettant de dire si un graphe contient un cycle.
Ce TP est inspiré du TD: TD2 et des TDs donnés au Licences Informatiques INF351 de l'Université Bordeaux 1.