TP 3 - tri topologique et composante fortement connexe
L'objectif de ce TP est de compléter le module de graphe en ajoutant un algorithme de tri topologique, et de calcul des composantes fortements connexes.
Exercice 1: calcul des composantes connexes d'un graphe
Rapeller ce qu'est le tri topologique d'un graphe.
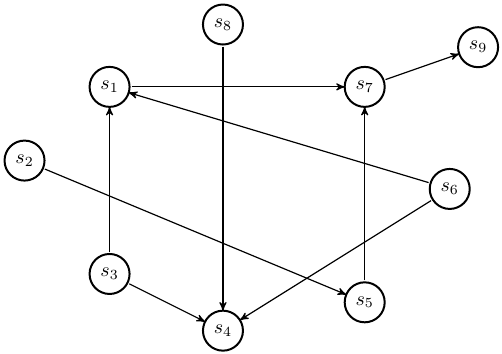
Appliquer l'algorithme de tri topologique basé sur l'algorithme PP au graphe ci-dessous en suivant l'ordre lexicographique:
Implémenter l'algorithme de tri topologique basé sur l'algorithme PP.
Rappel:
PP(G)
pour chaque sommet u de X faire
couleur[u] <- BLANC
pere[u] <- nil
temps <- 0
pour chaque sommet u de X faire
si couleur[u] = BLANC alors
Visiter_PP(u)
Visiter_PP(u)
couleur[u] <- GRIS
d[u] <- temps <- temps + 1
pour chaque v de Adj[u] faire
si couleur[v] = BLANC alors
pere[v] <- u
Visiter_PP(v)
couleur[u] <- NOIR
f[u] <- temps <- temps + 1
Exercice 2
Rapeller ce qu'est une composante fortement connexe.
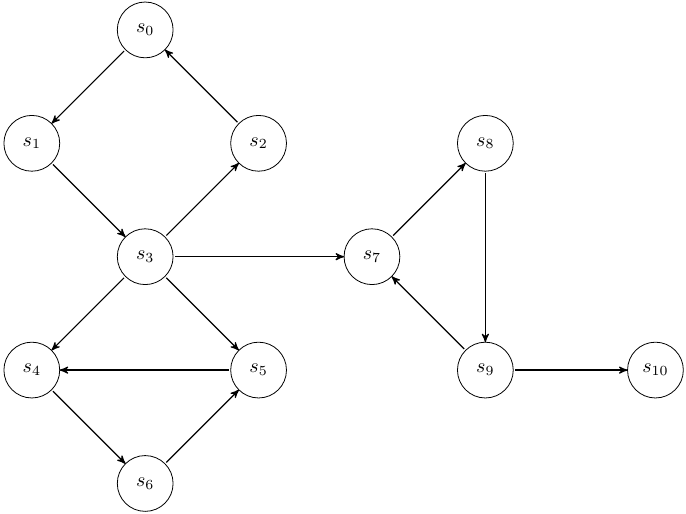
Appliquer l'algorithme de calcul des composantes fortement connexes au graphe ci-dessous:
Rappel:
Composantes_fortement_connexes(G):
D <- PP(G).
I <- inverse( D ).
F <- PP( I ) en considerant les sommets dans l'ordre decroissant des f(u) de D
Afficher les arborescences de la foret de F
Implémenter l'algorithme de calcul des composantes fortement connexes.
Exercice 3
Soit 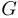 un graphe de sommets
un graphe de sommets 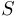 et d'arêtes
et d'arêtes 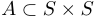 .
Le graphe réduit est le graphe dont les sommets sont les composantes fortement connexes
.
Le graphe réduit est le graphe dont les sommets sont les composantes fortement connexes 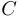 du graphe
du graphe 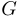 et les arêtes, les paires de sommets
et les arêtes, les paires de sommets 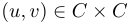 telles qu'il existe un arête
telles qu'il existe un arête 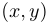 du graphe
du graphe 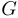 vérifiant que
vérifiant que 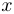 est un sommet de la composante fortement connexe
est un sommet de la composante fortement connexe 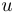 et
et 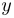 est un sommet de la composante fortement connexe
est un sommet de la composante fortement connexe 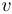 .
.
Déterminer le graphe réduit du graphe de l'exercice 1 et de l'exercice 2.
Donner un algorithme permettant de calculer le graphe réduit d'un graphe.
Implémenter cet algorithme.
Ce TP est inspiré du TP et des TDs donnés au Licences Informatiques INF351 de l'Université Bordeaux 1.