
[Retour à ma page personnelle] [English version]
Les "configurations de boucles compactes", ou Fully-packed loops (FPL) en Anglais, sont des objets fascinants, à la frontière de la physique statistique (le "modèle de la glace à 6 sommets") et des mathématiques (elles sont en bijection avec les "matrices à signes alternants", qui généralisent les matrices de permutation et interviennent dans des formules de calcul de déterminants dues à Dodgson (parfois plus connu sous le nom de Lewis Carroll).
Un FPL de taille N est un sous-graphe d'une grille carrée NxN, dont chaque sommet est de degré exactement 2. Les conditions au bord de la grille sont un peu particulières: un sommet sur deux, en alternance, a une arête sortante (donc degré 1 seulement dans la grille); les coins comptent comme deux sommets pour l'alternance.
Comme un petit dessin vaut souvent mieux qu'un long discours, voici l'un des 129534272700 FPL de taille 10, choisi aléatoirement, de manière uniforme, selon la méthode du "couplage venu du passé" (Coupling from the Past, CFTP).

Dans chaque FPL, les 2N arêtes du bord de la grille sont reliées entre elles par des chemins, formant un "couplage" (parfait, sans croisements) des 2N extrêmités. Sur ces couplages, dessinés dans un cercle, il est possible de choisir deux extrêmités adjacentes et de les "croiser":
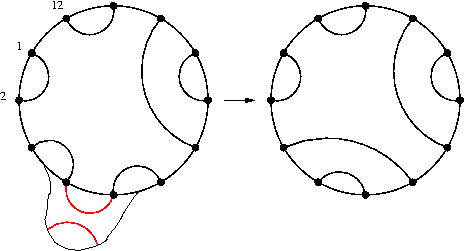
Il existe différentes conjectures sur le nombre de FPL représentant un couplage donné. La plus intriguante (à mon avis) peut être interprétée comme ceci: il est possible de définir sur les FPL de taille N, une chaîne de Markov laissant invariante la distribution uniforme, et qui, "projetée" sur les couplages, revienne à choisir deux extrêmités adjacentes et à leur appliquer l'opération de croisement (c'est en fait une affirmation sur la distribution stationnaire de la chaîne de Markov sur les couplages consistant à croiser deux brins adjacents choisis au hasard).
Une remarque naturelle est que les couplages ont une évidente symétrie de rotation, qui chez les FPL n'est pas du tout évidente (il faut "faire tourner" d'1/2N tour un carré...). Il se trouve qu'une telle symétrie existe pourtant: B. Wieland a exhibé une très jolie transformation bijective sur les FPL, qui a pour effet de "faire tourner d'un cran" le couplage sous-jacent. C'est cette bijection qui est illustrée ici, sur un FPL de taille 20.

(En fait, je triche: sur une image sur deux, les arêtes sortantes ne sont pas les bonnes, la figure est le complémentaire d'un FPL. Il faut donc faire deux pas pour avoir la rotation de Wieland, mais la transformation est bien bijective, et l'animation est plus lisible de cette manière)
La technique du "couplage depuis le passé" de Propp et Wilson s'applique fort bien aux FPL. Voici (au format PDF) une image d'un FPL de taille 100, tiré aléatoirement et de manière uniforme par cette méthode, avec une "boucle" distinguée en rouge.
Quelques autres images de FPL aléatoires, toutes obtenues par l'algorithme de Propp et Wilson:
[Retour à ma page personnelle] [English version]