
[Back to my homepage] [Version franšaise]
"Fully-packed loop configurations" (FPL) are fascinating objects with connections to statistical physics (the "6-vertex model") and mathematics (they are in one-to-one correspondence with "alternating-sign matrices", which generalize permutation matrices and appear in determinant formulae due do Dodgson.
An FPL of size N is a subgraph of an NxN square grid, where each vertex has degree exactly 2. Border conditions are defined as follows: half the border vertices, alternatively, have a single edge leaving the grid (which leaves only degree 1 inside the grid); corners count as two vertices for the border conditions.
As an example, here is one of the 129534272700 FPL of size 10, chosen uniformly at random using the "coupling from the past" (CFTP) technique.

In each FPL, the 2N border edges are connected to one another by paths, which define a (perfect, noncrossing) matching of the 2N endpoints. On each such matching, one can pick any two endpoints and "cross links":
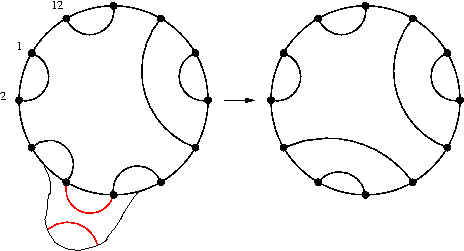
There are many conjectures on the number of FPL which show a given matching. One of them can be expresses as: there exists an ergodic Markov chain whose state space is the set of FPL of size N, whose stationary distribution is uniform, and which, when "projected" on the corresponding matchings, yields a new Markov chain whose steps correspond to picking (uniformly at random) two adjacent endpoints and crossing their links.
The Markov chain on matchings is obviously invariant by a rotation of 1/2N turn; that the distribution of matchings on FPLs has the same property was proved by B. Wieland, who described a very elegant bijection on FPLs which has the effect of "rotating" the matchings. This bijection is illustrated below on an FPL of size 20.

(I am cheating slightly here: in one frame out of two, the exterior edges are the wrong ones, and the picture is the complementary of a proper FPL. The animation is just easier to read this way.)
The "coupling from the past" technique due to Propp and Wilson can easily be applied to generate uniformly random FPLs, and this is how all the pictures on this page were obtained.
Here is a small gallery of pictures, all in PDF format:
[Back to my homepage] [Version franšaise]