Définition 5
Soit
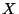
une variable aléatoire, l'opérateur d'
espérance
mathématique est défini par :
Proposition 1
Soit
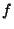
une fonction définie pour tout
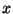
appartenant à l'ensemble de
définition de la variable aléatoire
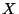
telle que
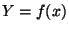
soit la variable
aléatoire transformée de
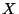
par la fonction
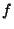
, alors :