


suivant: Caractéristiques de dispersion
monter: Caractérisques de position
précédent: Espérance
Définition 6
On appelle
moments d'odre 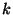
les quantités
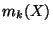
définies par :
La moyenne 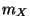 de la variable aléatoire
de la variable aléatoire 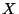 est le moment d'ordre
est le moment d'ordre  :
:
Propriétés de la moyenne
- -
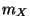 est une grandeur homogène à
est une grandeur homogène à 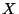
- -
- indicateur de position
- -
- renseigne sur l'ordre de grandeur des valeurs
prises par la variable aléatoire
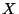 .
.
- -
- On appelle moments centrés les quantités
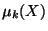 définies par :
définies par :
Pascal Ferraro
2002-11-22
![]() de la variable aléatoire
de la variable aléatoire ![]() est le moment d'ordre
est le moment d'ordre ![]() :
: